一种求多个矩形和周长(∪)的方法
扫描线:假设有一条扫描线从一个图形的下方扫向上方(或者左方扫到右方),那么通过分析扫描线被图形截得的线段就能获得所要的结果。该过程可以用线段树实现——洛谷题解
面积并
二话不说先上图——自己画图贼丑,所以暂且借一下洛谷的图

如何求上面两个矩形的面积呢??
我们假设一条扫描线从下方开始向上扫,扫到横边的时候停止、
首先我们将矩形的上下边分为上位边(即y坐标大的那条平行于x轴的边),和下位边(y坐标小的平行于x轴的边).然后我们把所有矩形的上下位边按照他们y坐标从小到大排序,可以得到4条扫描线:
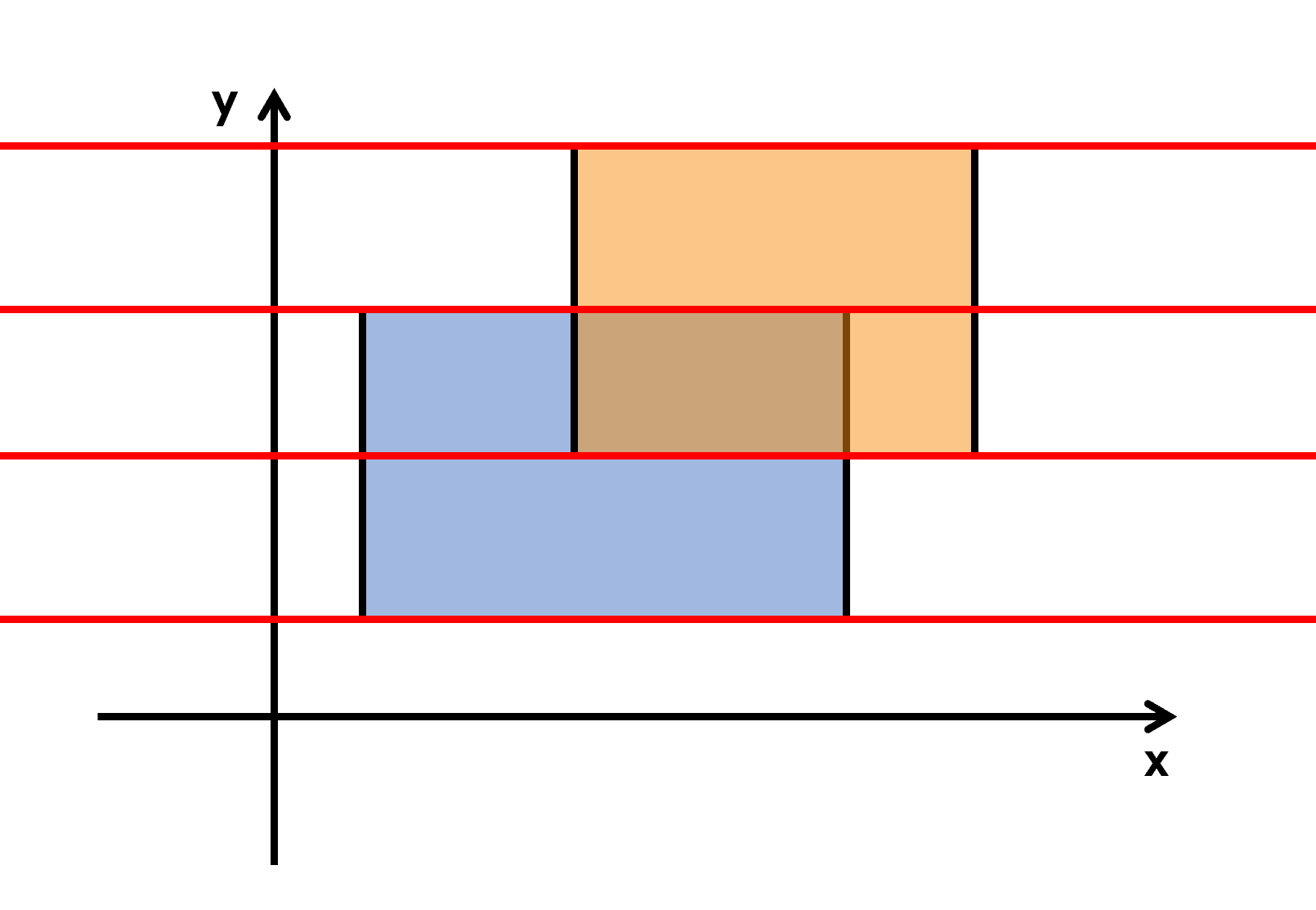
根据图可以看出,对图形面积有贡献的是横边左右端点的坐标,我们把矩形的下边赋予权值为1,上边为-1,然后把所有的边按照纵坐标大小升序排序(模拟扫描过程);

然后捏??
线段树是个好东西(每次都挂)
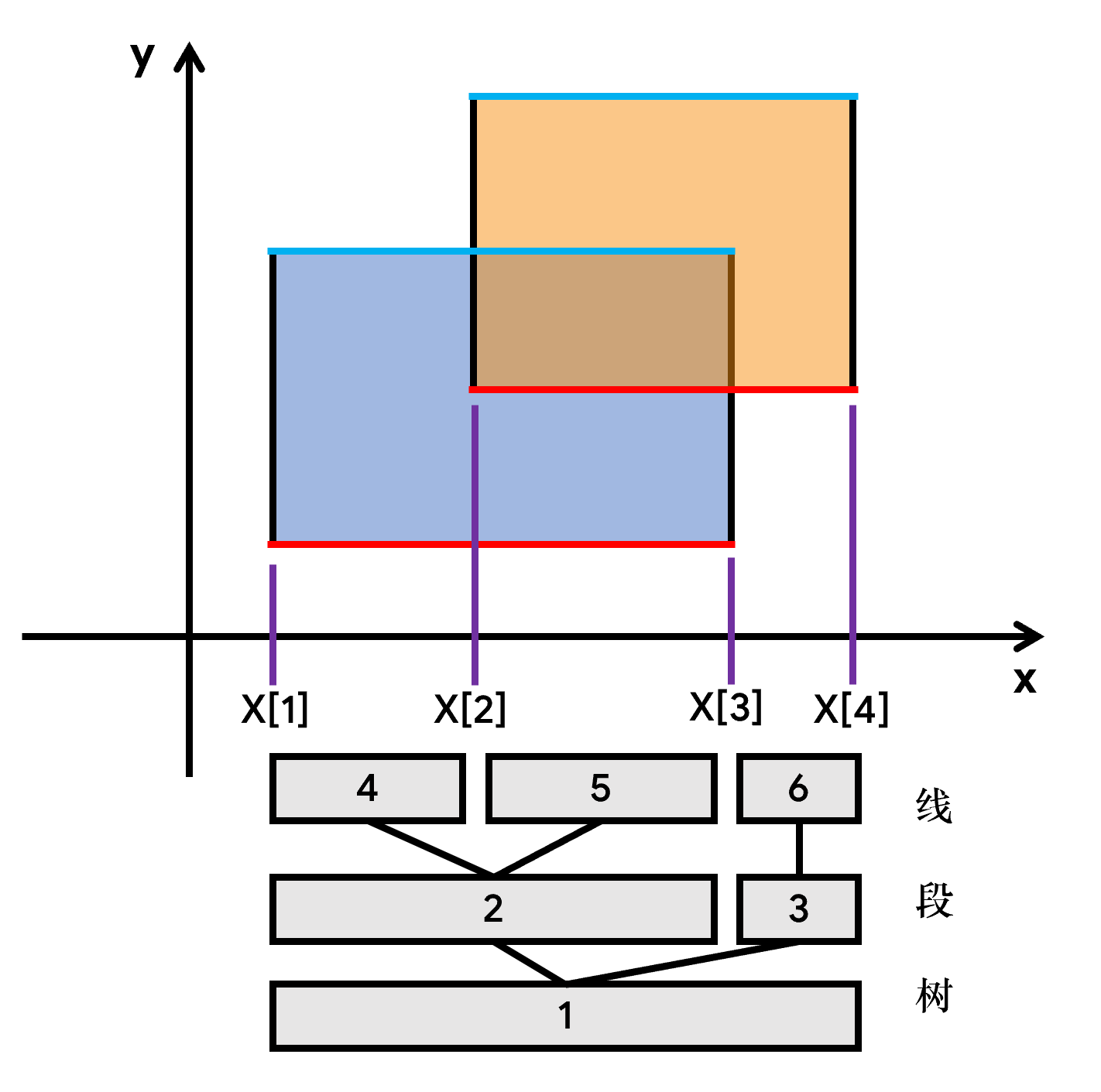
我们把所有的边离散化,把横坐标存到一个数组里,升序排列,然后去重(防止x为浮点数且很大无法进行线段树)

上图可以看出,四个横坐标把x轴分成了5段,我们取中间3段间线段树维护
其中每个端点维护每个线段信息:
1.该线段被覆盖了多少次(被多少个矩形所覆盖)
2.该线段内被整个图形所截的长度是多少
显然,只要一条线段被覆盖,那么它肯定被图形所截。所以,整个问题就转化为了一个区间查询问题,即:每次将 当前扫描线扫到的边 对应的信息 按照之前赋上的权值更新,然后再查询线段树根节点的信息,最后得到当前扫描线扫过的面积。这就可以用线段树来实现了
模拟过程
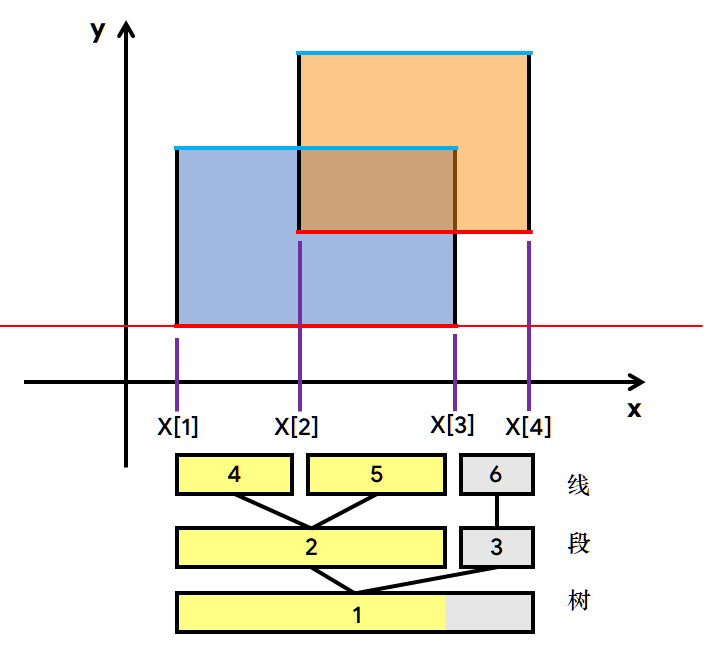


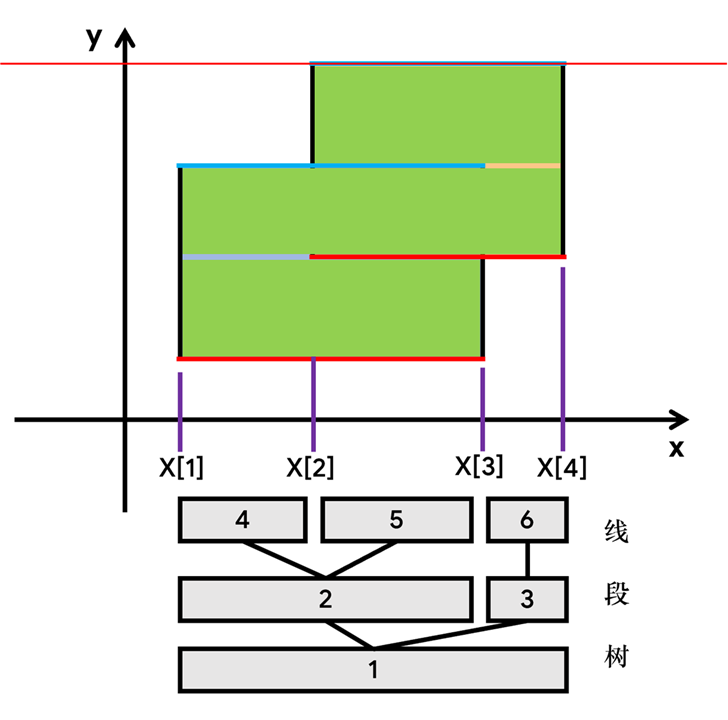
我们已经知道,这棵线段树的每个节点都对应了一条线段。考虑将线段树上节点对应的区间和横边建立映射关系。先看对于一个叶子节点(x),建树时保证了(tree[x].l=tree[x].r)但其保存的信息很显然不可能只是某条线段的一个端点(如果一条线段的两个端点重合,那么它实质上仅是一个点)。再看一个节点的左右儿子,同样地,建树的时候已经保证了左右儿子的区间不会重合(交集为空),但是看这样两条相邻线段:([1,2],[2,3])你会发现([1,2]∩[2,3]={2}),也就是说左儿子的右端点和右儿子的左端点其实是重合的。
考虑把线段树每个节点(x)对应的区间((tree[x].l,tree[x].r))不变,改变区间和横边的映射关系,具体为:节点(x)对应([X[tree[x].l],X[tree[x].r+1]])这条横边。可以看到,这里很机智地把右端点的对应关系给改了下,于是就兼容了