题目大意:
给定一张 $ n $ 个点 (m) 条边的无向图,每个点都有权值 (w_i),要处理 (q) 个操作
- 将某个点的权值修改
- 询问两点间路径中点的最小权值
$ 1leq m,q,n leq 10^5, 1leq w_ileq 10^9$
solution
知识点:圆方树
什么是圆方树
无向图,对于每个点双(任意两点都有两条路径可以到达),建一个方点,让方点和它对应的点双中的圆点连边。
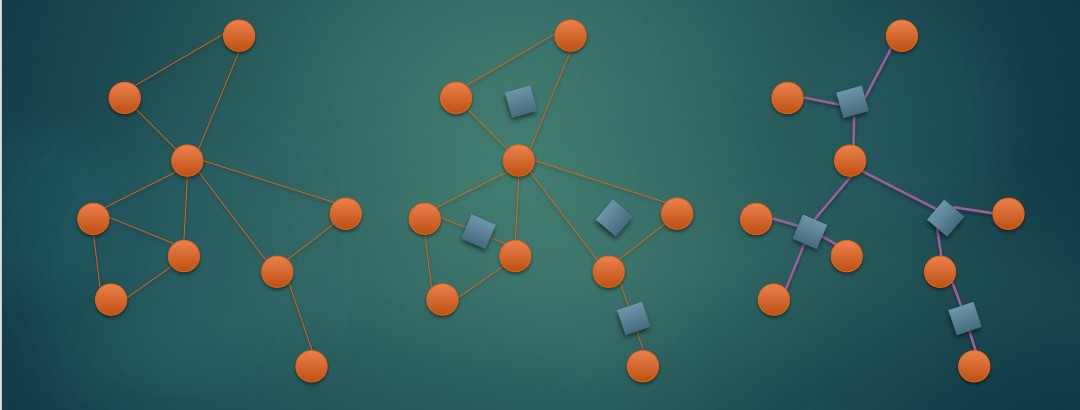
如何构建圆方树?
用 (tarjan) 求出每个点双,新建一个节点,连边就好了
因为是求路径上的最小值,可以考虑把方点的权值赋为所在点双中所有点权值的最小值,因为每次修改都要比较方点周围的所有点,所以遇见菊花图就很容易被卡成 (O(nq))
因为圆方树是一棵树,所以考虑树的性质,对于每个方点权值赋为它所有儿子权值的最小值,用 (multiset) 维护就好了
code
/*
work by:Ariel_
建立圆方树,方点开 multiset 存周围点的最小值,然后树剖求链上最小值就好了
*/
#include<iostream>
#include<cstdio>
#include<vector>
#include<set>
#define lson rt << 1
#define rson rt << 1|1
#define ll long long
#define rg register
using namespace std;
const int MAXN = 2e5 + 5;
const int INF = 0x3f3f3f3f;
int read(){
int x = 0,f = 1; char c = getchar();
while(c < '0'||c > '9') {if(c == '-') f = -1; c = getchar();}
while(c >= '0' && c <= '9') {x = x*10 + c - '0'; c = getchar();}
return x*f;
}
int n, m, q, w[MAXN], fcnt;
int fa[MAXN], dep[MAXN], siz[MAXN], son[MAXN], top[MAXN], id[MAXN], o, val[MAXN];
multiset<int> S[200010];
struct edge {int v, nxt;}e[MAXN << 1], E[MAXN << 1];
int Head[MAXN], head[MAXN], Ecnt, ecnt;
void Add_edge(int u, int v) {
E[++Ecnt] = (edge){v, Head[u]};
Head[u] = Ecnt;
}
void add_edge(int u, int v) {
e[++ecnt] = (edge) {v, head[u]};
head[u] = ecnt;
}
namespace Seg{
struct Tree {
int l, r, minn;
}tree[MAXN << 3];
void push_up(int rt) {
tree[rt].minn = min(tree[lson].minn, tree[rson].minn);
}
void build(int rt, int l, int r) {
tree[rt].l = l, tree[rt].r = r;
if (l == r) {
tree[rt].minn = w[val[l]];
return ;
}
int mid = (l + r) >> 1;
build(lson, l, mid), build(rson, mid + 1, r);
push_up(rt);
}
void update(int rt, int l, int r, int p, int k) {
if (tree[rt].l == tree[rt].r) {
tree[rt].minn = k;
return ;
}
int mid = (l + r) >> 1;
if (p <= mid) update(lson, l, mid, p, k);
else update(rson, mid + 1, r, p, k);
push_up(rt);
}
int query(int rt, int l, int r, int L, int R) {
if (L <= l && r <= R) return tree[rt].minn;
int ret = INF;
int mid = (l + r) >> 1;
if (L <= mid) ret = min(ret, query(lson, l, mid, L, R));
if (R > mid) ret = min(ret, query(rson, mid + 1, r, L, R));
return ret;
}
}
using namespace Seg;
namespace Cut{
void dfs(int x, int f) {
fa[x] = f, dep[x] = dep[f] + 1, siz[x] = 1;
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].v;
if (v == f) continue;
dfs(v, x);
siz[x] += siz[v];
if (siz[v] > siz[son[x]]) son[x] = v;
}
}
void dfs2(int x, int tp) {
top[x] = tp, id[x] = ++o, val[o] = x;
if (son[x]) dfs2(son[x], tp);
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].v;
if(v == fa[x] || v == son[x]) continue;
dfs2(v, v);
}
}
int Query(int x, int y) {//查询路径最小值
int ret = INF;
while(top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]]) swap(x, y);
ret = min(ret, query(1, 1, fcnt, id[top[x]], id[x]));
x = fa[top[x]];
}
if (dep[x] > dep[y]) swap(x, y);
ret = min(ret, query(1, 1, fcnt, id[x], id[y]));
if (x > n) ret = min(ret, w[fa[x]]);
return ret;
}
}
using namespace Cut;
int dfn[MAXN], low[MAXN], Stack[MAXN], tot, cnt;
void Tarjan(int x) {
dfn[x] = low[x] = ++tot;
Stack[++cnt] = x;
for (int i = Head[x]; i; i = E[i].nxt) {
int v = E[i].v;
if (!dfn[v]) {
Tarjan(v);
low[x] = min(low[x], low[v]);
if (low[v] == dfn[x]) {
fcnt++;//方点的个数
for (int j = 0; j != v; cnt--) {
j = Stack[cnt];
add_edge(fcnt, j), add_edge(j, fcnt);//方点和原点建边
}
add_edge(fcnt, x), add_edge(x, fcnt);//把最后一个点加上
}
}
else low[x] = min(low[x], dfn[v]);
}
}
char s[5];
int main(){
n = read(), m = read(), q = read();
for (int i = 1; i <= n; i++) w[i] = read();
for (int i = 1, u, v; i <= m; i++) {
u = read(), v = read();
Add_edge(u, v), Add_edge(v, u);
}
fcnt = n;
Tarjan(1), dfs(1, 0), dfs2(1, 1);
for (int i = 1; i <= n; i++)
if (fa[i]) S[fa[i]].insert(w[i]);//存每个点的儿子
for (int i = n + 1; i <= fcnt; i++) w[i] = *S[i].begin();//每个方点存周围点的最小值
build(1, 1, fcnt);
while(q--) {
scanf("%s", s + 1);
if (s[1] == 'C') {
int x = read(), y = read();
update(1, 1, fcnt, id[x], y);
if (fa[x]) {
S[fa[x]].erase(S[fa[x]].lower_bound(w[x]));
S[fa[x]].insert(y);
if (w[fa[x]] != *S[fa[x]].begin()) {
w[fa[x]] = *S[fa[x]].begin();
update(1, 1, fcnt, id[fa[x]], w[fa[x]]);
}
}
w[x] = y;
}
else if(s[1] == 'A'){
int x = read(), y = read();
printf("%d
", Query(x, y));
}
}
puts("");
return 0;
}