介绍
模板题,最早在数据结构中学习过,这次上贪心的课算是回顾了一下.主要有两个算法——prime和kruskal,这边做个记录,方便以后用.
来源
Description
在一张图上有N个点,点与点之间的连接的花费都已经告诉你了,请你设计一下,如何解决这个“最小生成树”的问题。要求用prim方法求解。
Input
首先输入一个数字N(0〈=N〈=100)
然后输入一个N*N的矩阵 其中第i行第j列的数字k表示从点i到点j需要的花费。
Output
一个数字,最少需要多少花费才能使得整张图任意两点都直接或者间接连通(也就是最小生成树的权)
Sample Input
5
0 41 67 34 0
41 0 69 24 78
67 69 0 58 62
34 24 58 0 64
0 78 62 64 0
0
2
0 1
1 0
Sample Output
116
0
1
分析问题:
-
什么是最小生成树?
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。 ——百度百科
特点:
- 连通性:连通图
- 无回路:有保持图联通的最少的边
- 边的权值之和最小:极小联通子图
接下来我们将讨论如何用prime算法和kruskal算法分别获得具有以上特定的树
-
prime算法
数据结构:
-
used[N]:记录节点是否被加入到生成树
类型:bool
注:如果已经被加入到生成树(也就是用过了),则置为true,否则置为false
-
dis[N]:用于计算当前生成树到其它原树上所有节点的距离
类型:int
注:
- 这里记录的是两个集合之间的关系
- 对于被当前生成树已经囊括的节点,距离可以标为0.但是由于used数组已经记录了这一点,在代码中实际上不需要这么做
操作:
- 选择一个点,更新对应的used数组和dis数组
- 每次从used=false的点中取出dis最小的点并更新used数组和dis数组
- 当所有sued都为true的时候退出
总结:
- 由于prime算法只对点进行操作,其复杂度与边数无关,适合点多的稠密图(点多的图)
- 其贪心思想主要表现在每次选取dis最小的点纳入
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <algorithm> #include <iostream> #define INF 0x3f3f3f3f using namespace std; const int N=1e2+10; int mp[N][N],dis[N]; bool used[N]; int prime(int n); int main() { //可能越界 int n; while(~scanf("%d",&n)){ memset(used,false,sizeof used); memset(dis,INF,sizeof dis); for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ scanf("%d",&mp[i][j]); if(mp[i][j]==0){ mp[i][j]=INF; } } } int ans = prime(n); printf("%d ",ans); } return 0; } int prime(int n){ int ans = 0; //总是从第一个点开始 used[1]=true; for(int i=1;i<=n;i++){ dis[i]=min(dis[i],mp[1][i]); } for(int i=1;i<=n-1;i++){ int temp=0; for(int i=1;i<=n;i++){ if(!used[i]&&dis[i]<dis[temp]){ temp = i; } } if(!temp){ break; } used[temp]=true; //cout << "temp:" << temp <<" dis[temp]:" << dis[temp] << endl; ans += dis[temp]; //更新dis for(int i=1;i<=n;i++){ if(!used[i]){ dis[i]=min(dis[i],mp[temp][i]); } } } used[1]=true; return ans; } -
-
kruskal算法
数据结构:
-
node[N]:用于存储边信息
类型:结构体(包括起始点,结束点,权值)
-
parent[N]:记录父节点,用于判断任意两个点是否在同一集合中
类型:int
注:主要用并查集进行操作,后面会展开讲,同时会给出具体的代码
操作:
- 对所有的边依权值排序
- 由小到大,依次对所有边进行遍历,判断边的起始点与结束点是否被纳入生成树集合以决定是否纳入
- 上面的算法看似简单,但是还有一个明显的问题就是如何判断两个点是否在同一个集合中,从而引出了并查集
并查集:
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示。
数据结构:int型parent[N]数组
操作:并查集常用的几个操作是初始化,查,并,对于查操作需要理解其优化的操作,important!
-
初始化
for(int i=1;i<=N;i++){ parent[i]=i; }注:显然一开始,每个节点都是其自身的父节点
-
查操作:查找某个节点的根节点
int find(int id){ if(id!=parent[id]){ parent[id]=find(parent[id]); } return parent[id]; }注:
-
这是一个递归的过程
-
通过parent[id]=find(parent[id])操作,我们在递归的回溯过程中可以直接将整个关系树"拉平"
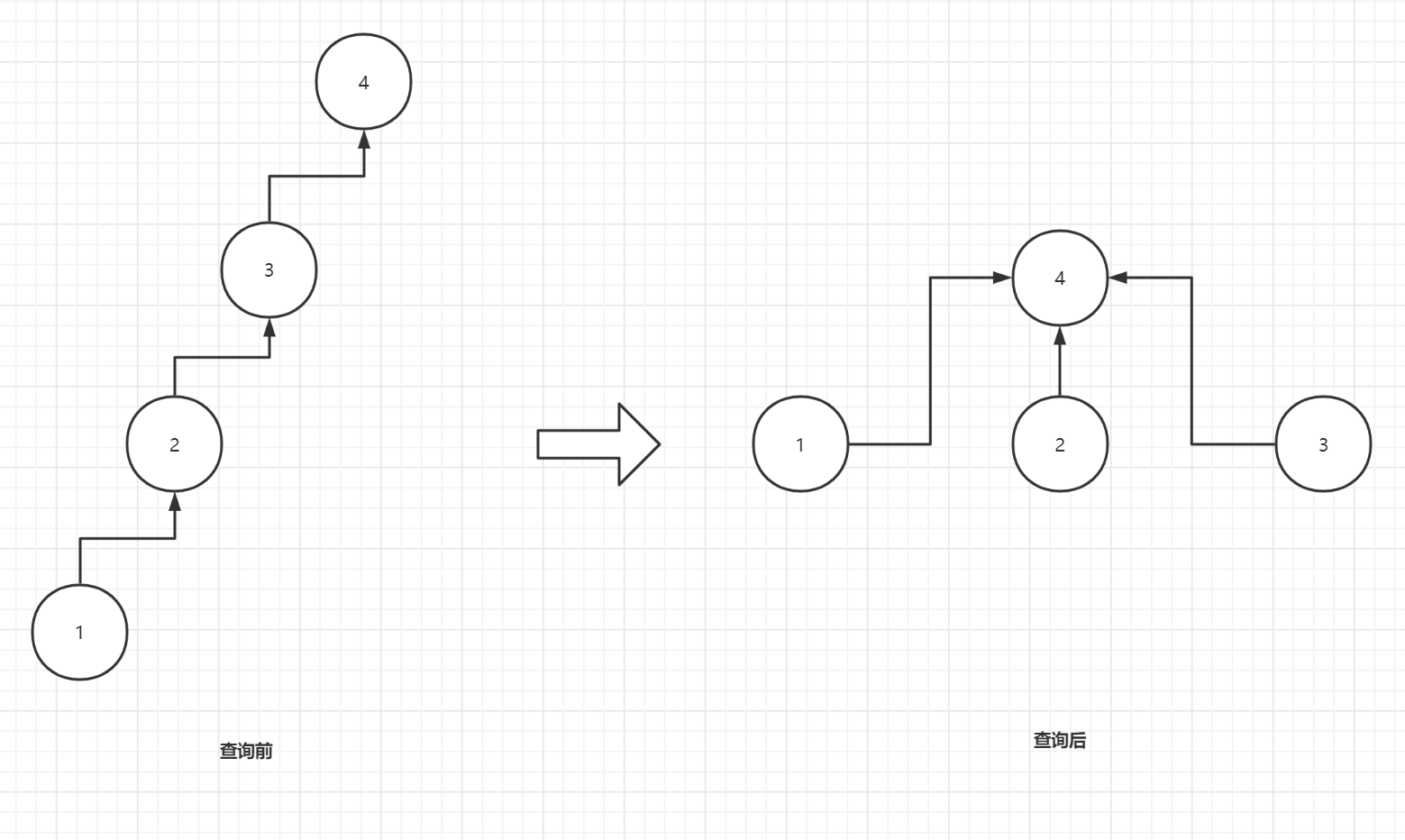
注:可以看到在一次查询之后,我们再次查询只需要O(1)的时间复杂度
-
-
并操作
void unionn(int a,int b){ int parentA=find(a); int parentB=find(b); if(parentA==parentB) return ; parent[parentA]=parentB; }注:可以看到并操作通过查操作完成的,其实还可以基于size或者deep对并操作进行优化,这里就不深入了
总结:
- kruskal算法主要是对边进行操作,其复杂度与边数有关,适合稀疏图
- 其贪心思想表现在将边按权重排序后才进行筛选
#include <stdio.h> #include <stdlib.h> #include <iostream> #include <algorithm> #define INF 0x3f3f3f3f using namespace std; const int N=1e3+10; typedef struct{ int from,to,weight; }Node; Node arr[N]; int parent[N],n; int kruskal(int n); int find(int id); int cmp(Node a,Node b); void unionn(int a,int b); int main() { while(~scanf("%d",&n)){ for(int i=1;i<=n;i++){ parent[i]=i; } int num=0; for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ num++; arr[num].from = i; arr[num].to = j; scanf("%d",&arr[num].weight); } } int res = kruskal(num); printf("%d ",res); } return 0; } int find(int id){ if(id!=parent[id]){ parent[id]=find(parent[id]); } return parent[id]; } void unionn(int a,int b){ int parentA=find(a); int parentB=find(b); if(parentA==parentB) return ; parent[parentA]=parentB; } int cmp(Node a,Node b){ return a.weight<b.weight; } int kruskal(int num){ int res = 0; sort(arr+1,arr+num+1,cmp); for(int i=1;i<=num;i++){ if(find(arr[i].from)!=find(arr[i].to)){ res += arr[i].weight; unionn(arr[i].from,arr[i].to); } } return res; } -