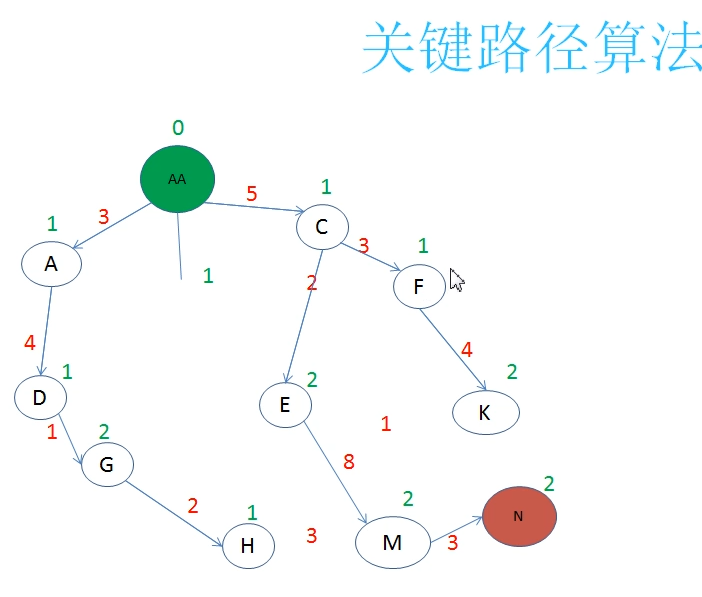
图
图由顶点和边 组成的一种结构G=(V,E )
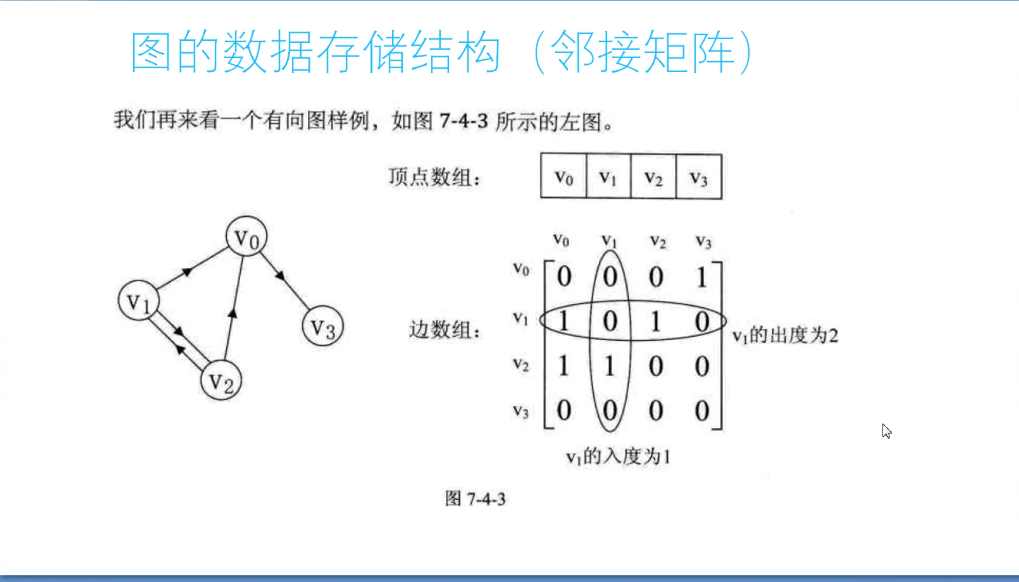
图的存储结构 (邻接矩阵)
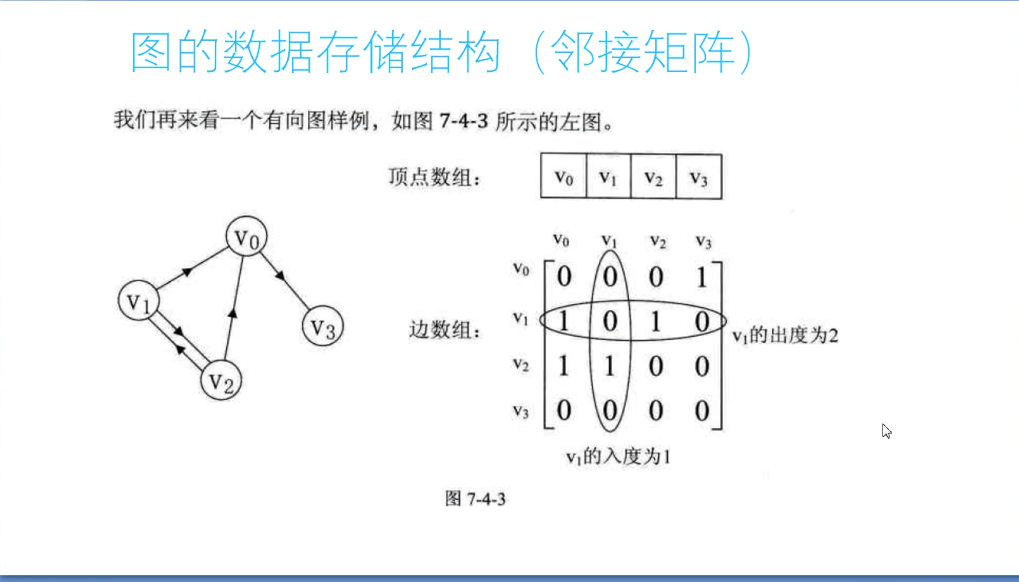
图的遍历
深度优先算法
随便走,等到无路可走,退回重新走,直到图被遍历完。
/*
* 定义图的结构
*/
public class Graph {
//节点数目
protected int size;
//定义数组,保存顶点信息
protected String[] nodes;
//定义矩阵保存顶点信息
protected int[][] edges;
/**
* A B C D E F G
* A 0 0 1 1 0 1 0
* B 0 0 1 0 0 0 0
* C 1 1 0 1 0 0 0
* D 1 0 1 0 0 0 0
* E 0 0 0 0 0 0 1
* F 1 0 0 0 0 0 1
* G 0 0 0 0 1 1 0
*/
public Graph(){
//初始化顶点
nodes = new String[]{"A","B","C","D","E","F","G"};
size=nodes.length;
//初始化边---- 为了直观,做一个常量定义
final int A=0,B=1,C=2,D=3,E=4,F=5,G=6;
edges = new int[size][size];
edges[A][C] = 1;
edges[A][D] = 1;
edges[A][F] = 1;
edges[B][C] = 1;
edges[C][A] = 1;
edges[C][D] = 1;
edges[C][B] = 1;
edges[D][A] = 1;
edges[D][C] = 1;
edges[E][G] = 1;
edges[F][A] = 1;
edges[F][G] = 1;
edges[G][F] = 1;
edges[G][E] = 1;
}
}
private int[] visit = new int[size]; //遍历标志,防止死环遍历
/**
* 深度优先遍历
* 一条路走到黑,不撞南墙不回头
* 对每一个可能的分支路径深入到不能再深入为止
*/
public void DeepFirst(int start) {//从第n个节点开始遍历
visit[start] = 1; //标记为1表示该顶点已经被处理过
System.out.println("齐天大圣到—>" + this.nodes[start]+"一游"); //输出节点数据
for (int i=0;i<this.size;i++){
if (this.edges[start][i] == 1 && visit[i]==0){
//邻接点
DeepFirst(i);
}
}
}
广度优先算法
访问节点所有可以到达的节点,再把访问到的节点的临界节点都找出来
/**
* 广度优先遍历
* 广度优先搜索遍历图的过程中以v 为起始点,由近至远,
* 依次访问和v 有路径相通且路径长度为1,2,…的顶点
* 第一批节点的邻接点,?
*/
private int[] queue = new int[size];
public void BreadthFirst(int front,int tail) {
int last = tail;
for (int index=front;index<=tail;index++){
int node = queue[index];
System.out.println("齐天大圣到—>" + this.nodes[node]+"一游"); //输出节点数据
//找出所有的邻接点
for (int i=0;i<this.size;i++){
if (this.edges[node][i] == 1 && visit[i]==0){
//邻接点
visit[i] = 1;
queue[++last] = i;
}
}
}
//遍历下一批节点
if (last > tail){
BreadthFirst(tail+1,last);
}
}
public void BreadthFirst(int start){
queue[0] = start;
visit[start] = 1;
BreadthFirst(0,0);
}
public static void main(String[] args) {
GraphCover graph = new GraphCover();
graph.BreadthFirst(0);
}
}
找出图中最短路径
得到图的最短路径树

迪杰斯特拉算法 Dijkstra
扩展知识
int i = Integer.Max_VALUE;
i= Integer.MAX_VALUE ,即 i = 2147483647,i再加1,就变成了-2147483648
package com.enjoy.graph;
public class Dijkstra {
//节点数目
protected int size;
//定义数组,保存顶点信息
protected String[] nodes;
//定义矩阵保存顶点信息
protected int[][] edges;
private int[] isMarked;//节点确认--中心标识
private String[] path;//源到节点的路径信息
private int[] distances;//源到节点的距离
public Dijkstra(){
init();
isMarked = new int[size];
path = new String[size];
distances = new int[size];
for (int i=0;i<size;i++){
path[i] = "";
distances[i] = Integer.MAX_VALUE;
}
}
public static void main(String[] args) {
Dijkstra dijkstra = new Dijkstra();
dijkstra.search(3);
}
public void search(int node){
path[node] = nodes[node];
distances[node] = 0;
do {
flushlast(node);
node = getShort();
}while (node != -1);
}
//1、扫描AA邻接点,记录邻接点权重值
private void flushlast(int node){
isMarked[node] = 1;
System.out.println(path[node]);
//扫描邻接点
for (int i=0;i<size;i++){
if (this.edges[node][i] > 0){
//计算AA节点到 i节点的权重值
int distant = distances[node] + this.edges[node][i];
if (distant < distances[i]){
distances[i] = distant;
path[i] = path[node] +"-->"+ nodes[i];
}
}
}
}
// 2、找出邻接点里最小的那个值
private int getShort(){
int last = -1;
int min = Integer.MAX_VALUE;
for (int i=0;i<size;i++){
if (isMarked[i] == 1){
continue;
}
if (distances[i] < min){
min = distances[i];
last = i;
}
}
return last;
}
public void init(){
//初始化顶点
nodes = new String[]{"AA","A","B","C","D","E","F","G","H","M","K","N"};
//节点编号-常量
final int AA=0,A=1,B=2,C=3,D=4,E=5,F=6,G=7,H=8,M=9,K=10,N=11;
size=nodes.length;
edges = new int[size][size];
edges[AA][A] = 3;
edges[AA][B] = 2;
edges[AA][C] = 5;
edges[A][AA] = 3;
edges[A][D] = 4;
edges[B][AA] = 2;
edges[B][C] = 2;
edges[B][G] = 2;
edges[B][E] = 3;
edges[C][AA] = 5;
edges[C][E] = 2;
edges[C][B] = 2;
edges[C][F] = 3;
edges[D][A] = 4;
edges[D][G] = 1;
edges[E][B] = 3;
edges[E][C] = 2;
edges[E][F] = 2;
edges[E][K] = 1;
edges[E][H] = 3;
edges[E][M] = 1;
edges[F][C] = 3;
edges[F][E] = 2;
edges[F][K] = 4;
edges[G][B] = 2;
edges[G][D] = 1;
edges[G][H] = 2;
edges[H][G] = 2;
edges[H][E] = 3;
edges[K][E] = 1;
edges[K][F] = 4;
edges[K][N] = 2;
edges[M][E] = 1;
edges[M][N] = 3;
edges[N][K] = 2;
edges[N][M] = 3;
}
}
工程施工图

- 发动机为关键节点(工程完成的时间取决于发动机节点完成的时间)
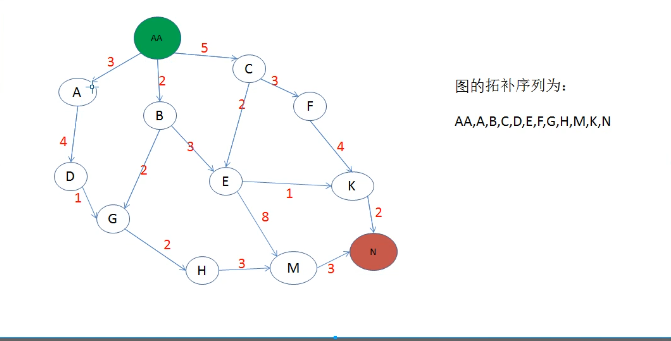
- 这种依赖图不能出现循环
分析图的依赖的问题,解决依赖问题
package com.enjoy.graph;
import java.util.Stack;
public class Aov {
//节点数目
protected int size;
//定义数组,保存顶点信息
protected String[] nodes;
//定义矩阵保存顶点信息
protected int[][] edges;
public Aov(){
init();
}
//入度数组
private int[] eSize;
private int[] fast;//最早时间
private int[] last;//最晚时间
public static void main(String[] args) {
Aov aov = new Aov();
aov.flush();
// int[] path = aov.getPath();
aov.exeKey();
}
public void exeKey(){
int[] path = getPath();
int start = path[0],end = path[size-1];
exeFast(start);
for (int i=0;i<size;i++){//初始化成工程最大值
last[i] = fast[end];
}
exeLast(end);
for (int i=0;i<size;i++){
int node = path[i];
if (fast[node] == last[node]){
System.out.print("--->"+nodes[node]);
}
}
System.out.println();
}
private void exeFast(int node){
for (int i=0;i<size;i++){
if (this.edges[node][i] > 0){
int cost = fast[node] + this.edges[node][i];
if (cost > fast[i]){
fast[i] = cost;
exeFast(i);
}
}
}
}
private void exeLast(int node){
for (int i=0;i<size;i++){
if (this.edges[i][node] > 0){
int cost = last[node] - this.edges[i][node];
if (cost < last[i]){
last[i] = cost;
exeLast(i);
}
}
}
}
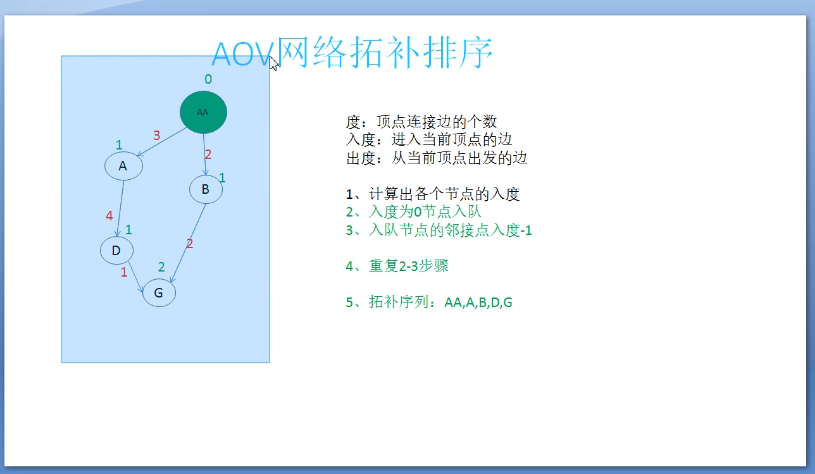
//1、计算出各个节点的入度
private void flush(){
eSize = new int[size];
for (int node=0;node<size;node++){
for (int i=0;i<size;i++){
if (edges[i][node] > 0){
eSize[node]++;
}
}
}
}
private int[] getPath(){
int count = 0;
int[] path = new int[size];
// 2、入度为0节点入队
// Queue<Integer> queue = new LinkedList<>();
Stack<Integer> stack = new Stack<>();
for (int i=0;i<size;i++){
if (eSize[i] == 0){
// queue.offer(i);
stack.push(i);
}
}
// 3、入队节点的邻接点入度-1
while (!stack.empty()){
Integer node = stack.pop();
// System.out.print("---->"+nodes[node]);
path[count++] = node;
for (int i=0;i<size;i++){
if (this.edges[node][i] > 0){
eSize[i]-- ;
if (eSize[i] == 0){
// queue.offer(i);
stack.push(i);
}
}
}
}
return path;
}
public void init(){
//初始化顶点
nodes = new String[]{"AA","A","B","C","D","E","F","G","H","M","K","N"};
//节点编号-常量
final int AA=0,A=1,B=2,C=3,D=4,E=5,F=6,G=7,H=8,M=9,K=10,N=11;
size=nodes.length;
fast = new int[size];
last = new int[size];
edges = new int[size][size];
edges[AA][A] = 3;
edges[AA][B] = 2;
edges[AA][C] = 5;
edges[A][D] = 4;
edges[B][G] = 2;
edges[B][E] = 3;
edges[C][E] = 2;
edges[C][F] = 3;
edges[D][G] = 1;
edges[E][K] = 1;
edges[E][M] = 8;
edges[F][K] = 4;
edges[G][H] = 2;
edges[H][M] = 3;
edges[K][N] = 2;
edges[M][N] = 3;
}
}
关键路径