题目描述Description
给你6个数,m, a, c, x0, n, g
Xn+1 = ( aXn + c ) mod m,求Xn
m, a, c, x0, n, g<=10^18
输入描述Input Description
一行六个数 m, a, c, x0, n, g
输出描述Output Description
输出一个数 Xn mod g
样例输入Sample Input
11 8 7 1 5 3
样例输出Sample Output
2
数据范围及提示Data Size & Hint
int64按位相乘可以不要用高精度。
题目分析
典型的矩阵快速幂问题。由递推式 Xn+1 = ( aXn + c ) mod m 可以构造出矩阵方程:
那么题目所求就可转化为一个1*2矩阵与n个二阶方阵的矩阵链乘。根据矩阵乘法的结合律,可得出:

即可转化为矩阵快速幂问题。其中的乘法运算已改为了倍增取模乘法。
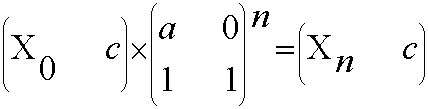 1 //WikiOI 1281 Xn数列
1 //WikiOI 1281 Xn数列
2 #include <iostream>
3 using namespace std;
4 typedef long long LL;
5 LL m, a, c, x0, n, MOD;
6 LL mlti(LL a, LL b) //倍增取模乘法
7 {
8 a %= m;
9 LL ans = 0;
10 while(b)
11 {
12 if(b & 1)ans = (ans + a)% m;
13 a = (a << 1)% m;
14 b >>= 1;
15 }
16 return ans;
17 }
18 struct Matrix2
19 {
20 LL val[2][2];
21 Matrix2(LL k1,LL k2,LL k3,LL k4)
22 {
23 val[0][0] = k1; val[0][1] = k2; val[1][0] = k3; val[1][1] = k4;
24 }
25 void Mlti(Matrix2 &m) //矩阵乘法
26 {
27 LL v1 = mlti(val[0][0],m.val[0][0])+mlti(val[0][1],m.val[1][0]);
28 LL v2 = mlti(val[0][0],m.val[0][1])+mlti(val[0][1],m.val[1][1]);
29 LL v3 = mlti(val[1][0],m.val[0][0])+mlti(val[1][1],m.val[1][0]);
30 LL v4 = mlti(val[1][0],m.val[0][1])+mlti(val[1][1],m.val[1][1]);
31 val[0][0] = v1,val[0][1] = v2,val[1][0] = v3,val[1][1] = v4;
32 }
33 };
34
35 int main()
36 {
37 ios::sync_with_stdio(0); //感谢陈思学长!
38 cin >>m >>a >>c >>x0 >>n >>MOD;
39 Matrix2 M(a, 0, 1, 1);
40 Matrix2 ans = M;
41 n -= 1;
42 while(n)
43 {
44 if(n & 1) ans.Mlti(M);
45 M.Mlti(M);
46 n >>=1;
47 }
48 cout << ((mlti(x0, ans.val[0][0])+mlti(c, ans.val[1][0]))%m)%MOD;
49 return 0;
50 }
那么题目所求就可转化为一个1*2矩阵与n个二阶方阵的矩阵链乘。根据矩阵乘法的结合律,可得出:

即可转化为矩阵快速幂问题。其中的乘法运算已改为了倍增取模乘法。
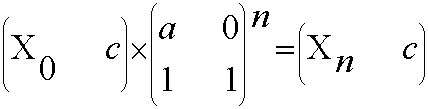
1 //WikiOI 1281 Xn数列
2 #include <iostream>
3 using namespace std;
4 typedef long long LL;
5 LL m, a, c, x0, n, MOD;
6 LL mlti(LL a, LL b) //倍增取模乘法
7 {
8 a %= m;
9 LL ans = 0;
10 while(b)
11 {
12 if(b & 1)ans = (ans + a)% m;
13 a = (a << 1)% m;
14 b >>= 1;
15 }
16 return ans;
17 }
18 struct Matrix2
19 {
20 LL val[2][2];
21 Matrix2(LL k1,LL k2,LL k3,LL k4)
22 {
23 val[0][0] = k1; val[0][1] = k2; val[1][0] = k3; val[1][1] = k4;
24 }
25 void Mlti(Matrix2 &m) //矩阵乘法
26 {
27 LL v1 = mlti(val[0][0],m.val[0][0])+mlti(val[0][1],m.val[1][0]);
28 LL v2 = mlti(val[0][0],m.val[0][1])+mlti(val[0][1],m.val[1][1]);
29 LL v3 = mlti(val[1][0],m.val[0][0])+mlti(val[1][1],m.val[1][0]);
30 LL v4 = mlti(val[1][0],m.val[0][1])+mlti(val[1][1],m.val[1][1]);
31 val[0][0] = v1,val[0][1] = v2,val[1][0] = v3,val[1][1] = v4;
32 }
33 };
34
35 int main()
36 {
37 ios::sync_with_stdio(0); //感谢陈思学长!
38 cin >>m >>a >>c >>x0 >>n >>MOD;
39 Matrix2 M(a, 0, 1, 1);
40 Matrix2 ans = M;
41 n -= 1;
42 while(n)
43 {
44 if(n & 1) ans.Mlti(M);
45 M.Mlti(M);
46 n >>=1;
47 }
48 cout << ((mlti(x0, ans.val[0][0])+mlti(c, ans.val[1][0]))%m)%MOD;
49 return 0;
50 }
2 #include <iostream>
3 using namespace std;
4 typedef long long LL;
5 LL m, a, c, x0, n, MOD;
6 LL mlti(LL a, LL b) //倍增取模乘法
7 {
8 a %= m;
9 LL ans = 0;
10 while(b)
11 {
12 if(b & 1)ans = (ans + a)% m;
13 a = (a << 1)% m;
14 b >>= 1;
15 }
16 return ans;
17 }
18 struct Matrix2
19 {
20 LL val[2][2];
21 Matrix2(LL k1,LL k2,LL k3,LL k4)
22 {
23 val[0][0] = k1; val[0][1] = k2; val[1][0] = k3; val[1][1] = k4;
24 }
25 void Mlti(Matrix2 &m) //矩阵乘法
26 {
27 LL v1 = mlti(val[0][0],m.val[0][0])+mlti(val[0][1],m.val[1][0]);
28 LL v2 = mlti(val[0][0],m.val[0][1])+mlti(val[0][1],m.val[1][1]);
29 LL v3 = mlti(val[1][0],m.val[0][0])+mlti(val[1][1],m.val[1][0]);
30 LL v4 = mlti(val[1][0],m.val[0][1])+mlti(val[1][1],m.val[1][1]);
31 val[0][0] = v1,val[0][1] = v2,val[1][0] = v3,val[1][1] = v4;
32 }
33 };
34
35 int main()
36 {
37 ios::sync_with_stdio(0); //感谢陈思学长!
38 cin >>m >>a >>c >>x0 >>n >>MOD;
39 Matrix2 M(a, 0, 1, 1);
40 Matrix2 ans = M;
41 n -= 1;
42 while(n)
43 {
44 if(n & 1) ans.Mlti(M);
45 M.Mlti(M);
46 n >>=1;
47 }
48 cout << ((mlti(x0, ans.val[0][0])+mlti(c, ans.val[1][0]))%m)%MOD;
49 return 0;
50 }