#4051. 买不到的数目

题目来源：

http://www.51cpc.com/problem/4051

题目描述

小明开了一家糖果店。他别出心裁：把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。 小朋友来买糖的时候，他就用这两种包装来组合。当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。 你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。 本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式

输入两个正整数

输出格式

输出不能最大组合的数字

样例

Sample input

4 7

Sample Output

17

题目思路

像要你求最大，最小之类的题目大多数都是有技巧而言的，例如我们以后会碰到的贪心、动态规划、数论等思想。所以说我们要用数学的思维去找出最简单的方法。

要是硬解的话网上也有一大堆题解和对于数论公式的证明，那我重新写一遍也没什么意义了。

我是初学者，数论什么什么的都不知道，我只是隐隐约约的感觉到这个应该和什么公式有关。

然后我就用找规律的方法把它写出来了。

首先，先暴力一小部分，输出所有结果，

当然，写的时候也不是那么顺利，因为存在无解的情况存在，所以陷入了无限循环，然后我将将那些肯定不存在的情况排除了。

然后就出现了

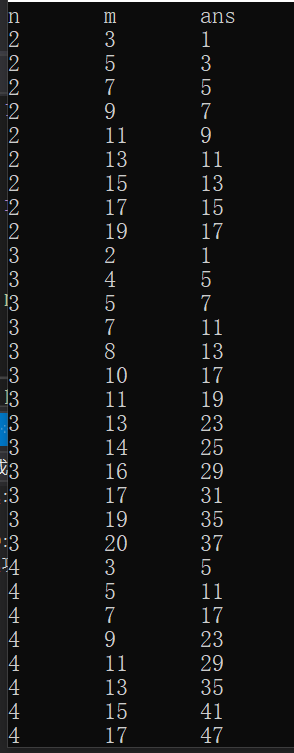
 我们要寻找的是ans=f(n,m)，这样的函数；

通过不断试验发现：ans= n * m - n - m;

那么我们直接输出公式就好了。

#include <stdio.h>

bool find(int m, int p, int q) {
    for(int i=0;i<1000;i++)
        for (int j = 0;j<1000;j++) 
            if (p * i + j * q == m) return true;
    return false;
}

int main()
{

    printf("n	m	ans
");
    for (int i = 2;i <= 20;i++)
        for (int j = 2;j <= 20;j++)
            for (int k = 1000;k >= 0;k--)
                if (!find(k, i, j)) {
                    if (k >= 999) break;
        //模拟的时候发现那些无解的数都符合这个条件，所以就用这个将其排除掉。
                    printf("%d	%d	%d
", i, j, k);
                    break;
                }

    return 0;
}

#include <stdio.h>
int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    printf("%d
", n * m - n - m);
    return 0;
}

如果您觉得不错就点个推荐或者收藏吧！

此题为分支，其根为：https://www.cnblogs.com/Attacking-vincent/p/12721609.html