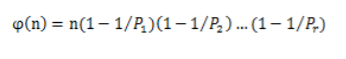非对称加密-RSA
1.1任务描述
任务描述某人相对少量需要传输的数据进行较高水平的加密，并不在意速度的快慢，他该怎么做？
1.2课程目标
- 了解非对称加密的概念和优缺点。
- 了解RSA的概念。
- 了解RSA算法。
- 学会使用RSA工具加解密。
1.3什么是非对称加密
1.3.1非对称加密简介
非对称加密简介对称加密算法在加密和解密时使用的是同一个秘钥；而非对称加密算法需要两个密钥来进行加密和解密，这两个秘钥是公开密钥（public key，简称公钥）和私有密钥（private key，简称私钥）。
1976年，美国学者Dime和Henman为解决信息公开传送和密钥管理问题，提出一种新的密钥交换协议，允许在不安全的媒体上的通讯双方交换信息，安全地达成一致的密钥，这就是“公开密钥系统”。
与对称加密算法不同，非对称加密算法需要两个密钥：公开密钥（publickey）和私有密钥（privatekey）。公开密钥与私有密钥是一对，如果用公开密钥对数据进行加密，只有用对应的私有密钥才能解密；如果用私有密钥对数据进行加密，那么只有用对应的公开密钥才能解密。因为加密和解密使用的是两个不同的密钥，所以这种算法叫做非对称加密算法。
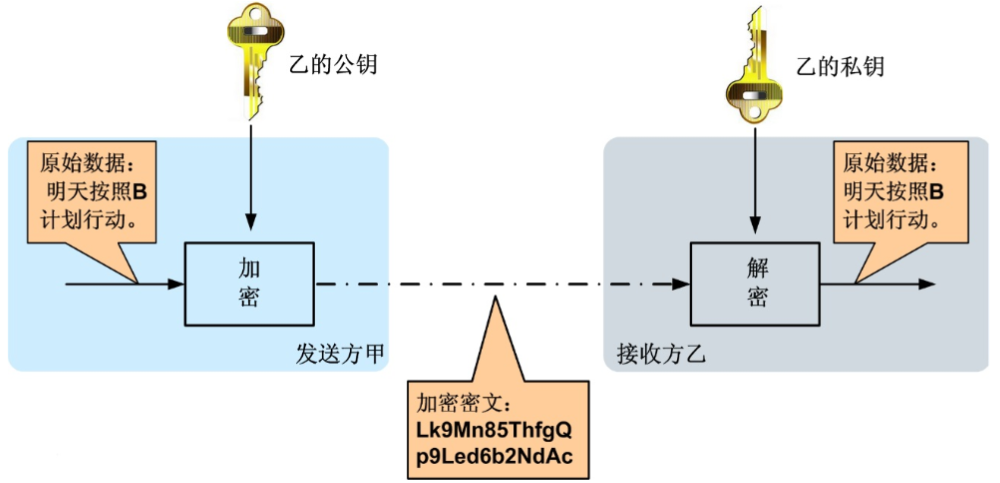
图3.1 非对称加密
1.3.2非对称加密的优缺点
非对称加密与对称加密相比，其安全性更好：对称加密的通信双方使用相同的秘钥，如果一方的秘钥遭泄露，那么整个通信就会被破解。而非对称加密使用一对秘钥，一个用来加密，一个用来解密，而且公钥是公开的，秘钥是自己保存的，不需要像对称加密那样在通信之前要先同步秘钥。
非对称加密的缺点是加密和解密花费时间长、速度慢，只适合对少量数据进行加密。
1.4RSA简介
RSA加密算法是一种非对称加密算法。在公开密钥加密和电子商业中RSA被广泛使用。RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。
1973年，在英国政府通讯总部工作的数学家克利福德·柯克斯（Clifford Cocks）在一个内部文件中提出了一个相同的算法，但他的发现被列入机密，一直到1997年才被发表。
对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用RSA加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA钥匙才可能被强力方式解破。到目前为止，世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被解破的。
1983年麻省理工学院在美国为RSA算法申请了专利。这个专利2000年9月21日失效。由于该算法在申请专利前就已经被发表了，在世界上大多数其它地区这个专利权不被承认。
1.5RSA算法
非对称算法的在应用的过程如下，假设发送方向接收方发送消息（明文）：
1、接收方生成公钥和私钥，公钥公开，私钥保留；
2、发送方将要发送的消息采用公钥加密，得到密文，然后将密文发送给接收方；
3、接收方收到密文后，用自己的私钥进行解密，获得明文。
可以看出，非对称加密解决了对称加密密钥传输的问题。
1.5.1数学基础
1.5.1.1 互质关系
1、素数
素数又称质数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数。
2、互质数
公因数只有1的两个数，叫做互质数；又称互素，若N个整数的最大公因子是1，则称这N个整数互质。
判断互质的简单法则：
a.任意两个质数是互质的；
b.一个数是质数，另一个数不是它的倍数，两者互质（比如正整数P是质数，则小于P的正整数和P都是互质的）；
c.两个不相等的数，较大的那个数是质数，两者互质；
d.1和任意自然数互质；
e.2和任何奇数是互质；
f.如果P是大于1的整数，则P和P-1互质；
g.如果P是大于1的奇数，则P和P-2互质。
1.5.1.2 欧拉函数
欧拉函数的意义在于计算在小于等于任意正整数n的正整数中，有多少个与n互质的正整数。
1.5.1.3 欧拉定理
1.5.1.4 模反元素
如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1。这时b被称为a的模反元素。公式如下：
1.5.1.5 扩展欧几里得算法
欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：
gcd函数就是用来求(a,b)的最大公约数的。
gcd函数的基本性质：
gcd(a,b)=gcd(b,a)=gcd(-a,b)=gcd(|a|,|b|)
对于不完全为 0 的非负整数 a，b，gcd(a,b)表示 a，b 的最大公约数，必然存在整数对 x，y ，使得 gcd(a,b)=ax+by。
1.5.2秘钥的生成与加解密
图3.2 RSA密钥生成与加解密
1.5.2.1 秘钥的生成
密钥生成的步骤如下：
1、随机选择两个不相等的质数p和q；
1.5.2.2 加密和解密
