多项式学习笔记

zoukankan html css js c++ java

多项式学习笔记
多项式学习笔记

$\LaTeX$ 过多警告 ⚠

学多项式了，~~由于肯定会忘~~所以来写笔记了，同时边学边写算加深记忆吧。这边还是用上次网络流笔记的格式。

下文中角度均以弧度制表示。

一、前置芝士知识

$~~~~$ 1.多项式：称一个关于 $x$ 的式子：

\[\large f(x)=\sum_{i=0}^na_i\times x^i \]
$~~~~$ 为 $\pmb{n}$ 次多项式，$a_i$ 为 $\pmb{i}$ 次项系数（是一个常数），$n$ 为该多项式的次数。

$~~~~$ 由上面的定义，我们也可以把 $n$ 次多项式记为一个 $n$ 次函数 $y=f(n)$ 。

$~~~~$ 而我们知道，给出 $(n+1)$ 个点的坐标，此时可以确定一个 $n$ 次函数的解析式。（由于一个 $n+1$ 元的非无解线性方程组有唯一解的必要条件是有 $n$ 个本质不同的方程）

$~~~~$ 综上，我们可以用两种方式来记一个多项式：

$~~~~ ~~~~$ 1.1 系数表示法：写成上面那个式子的形式。

$~~~~ ~~~~$ 1.2 点值表示法：给出 $(n+1)$ 个互不相同，且能形成非无解的方程组的点的坐标。

$~~~~$ 2.多项式运算

$~~~~$ 为了方便，我们假定下面进行运算的两个多项式 $A(x)=\sum_{i=0}^n a_i\times x^i$，$B(x)=\sum_{i=0}^nb_i\times x^i$ 的次数均为 $n$ 。（不足的一个不足部分的系数就是 $0$ ）

$~~~~ ~~~~$ 2.1 多项式加减法：

\[\large f(x)=A(x) \pm B(x)=\sum_{i=0}^n(a_i\pm b_i)\times x^i \]
$~~~~ ~~~~$ 乘法分配律，显然。

$~~~~ ~~~~$ 2.2 多项式乘法：

\[\large f(x)=A(x)\times B(x)=\sum_{i=0}^{n} \sum_{j=0}^n a_i\times b_j\times x^{i+j}=\sum_{i=0}^{2n}\sum_{j=0}^{\min(n,i)} a_{j}\times b_{i-j}\times x^i \]
$~~~~ ~~~~$ ~~这个也很显然吧~~，还是乘法分配律，多用几遍而已。

$~~~~ ~~~~$ 2.3 点值表示法下运算

$~~~~ ~~~~$ 首先，取可以表示多项式 $A$ 的 $(n+1)$ 个点，并取相同横坐标的，能表示多项式 $B$ 的 $(n+1)$ 个点。

$~~~~ ~~~~$ 之后，将两个横坐标相等的点的纵坐标直接加/减/乘就可以得到结果的多项式的点值表示。（由于多项式的运算也可以看作两个多项式值的运算。）

$~~~~ ~~~~$ 需要注意的是，由于乘法产生的多项式最高次数为 $2n$ ，所以初始应该取 $2n+1$ 个点。

$~~~~$ 3.复数

$~~~~$ 定义常数 $\pmb i$ 为虚根，满足：

\[i^2=-1 \]
$~~~~$ 则所有形如：

\[z=a+bi\ \ \ \ a,b\in R \]
$~~~~$ 的数 $z$ 被称作复数，同时所有复数组成的集合为复数集，记作 $C$.

$~~~~$ 特殊地，当 $\pmb{b \not = 0}$ 时，这样的数称为虚数，这样的数不能在数轴上表示，因为找不到它的相对大小。

$~~~~$ 称复数 $z=a+bi$ 中，$a$ 为 $z$ 的实部，$b$ 为 $z$ 的虚部。

$~~~~$ 4.复平面

$~~~~$ 一个平面直角坐标系，由互相垂直的横轴（即实轴）与纵轴（即虚轴）组成。

$~~~~$ 对于一个复数 $z=a+bi$ ，它可以在复平面上表示为一个从 $(0,0)$ 指向 $(a,b)$ 的向量。

$~~~~$ 而一个从 $(0,0)$ 指向 $(a,b)$ 的向量也一定唯一对应一个 $z=a+bi$ 的向量。~~这个很显然吧。~~

$~~~~$ 特殊地，当向量指向的点纵坐标为 $0$ 时，它表示一个实数。

$~~~~$ 记以横轴为始边，复数 $\pmb z$ 对应的向量 $\pmb Z$ 为终边的有向正角为复数 $z$ 的幅角。

$~~~~$ 注：正角为始边逆时针旋转使得其与终边重合的角度 $\theta$，负角为始边顺时针旋转使得其与终边重合的角度 $\theta$ 的相反数。

$~~~~$ 举个例子：

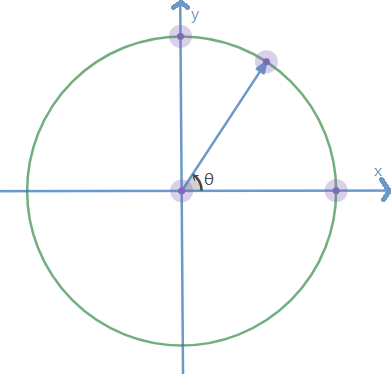
$~~~~$ 上图的 $\theta$ 就是幅角。

$~~~~$ 5.相关定义

$~~~~$ 以下设复数 $z=a+bi$ 。

$~~~~ ~~~~$ 5.1 复数的模： 一个复数的模为它在复平面上对应向量的长度，$z$ 的模记作 $|z|$ 。距离公式得：

\[|z|=\sqrt{a^2+b^2} \]
$~~~~ ~~~~$ 5.2 共轭复数： 两个复数若实部相等，虚部互为相反数，则它们互为共轭复数。记 $z$ 的共轭复数为 $\overline z$ 。

$~~~~ ~~~~$ 设 $z$ 的幅角为 $\theta_1$ ，$\overline z$ 的幅角为 $\theta_2$ 。则：

\[\theta_1+\theta_2=2\pi\\ |z|=|\overline z| \]
$~~~~ ~~~~$ 5.3 复平面上共轭复数： 两共轭复数对应的向量在复平面上关于横轴对称。因此不难发现上面关于幅角和的性质：

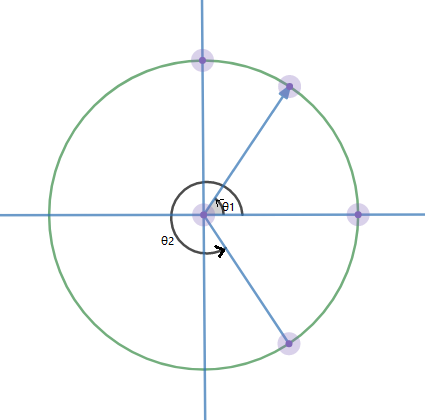
$~~~~$ 6 复数加减法

$~~~~ ~~~~$ 6.1 代数加减 ：设 $z_1=a+bi,z_2=x+yi$ ，则 $z_1\pm z_2=(a\pm x)+(b \pm y)i$ 。

$~~~~ ~~~~$ 6.2 复平面上加减 ：既然两个复数已经被表示为向量了，那向量加减直接使用平行四边形定则即可。~~什么，你说你不会？物理必修一第二章欢迎您~~

$~~~~$ 7 复数乘法

$~~~~ ~~~~$ 7.1 代数乘法： 仍然设 $z_1=a+bi$，$z_2=x+yi$ ，那么：

\[z_1\times z_2=(a+bi)\times (x+yi)\\ =ax+(ay+bx)i+byi^2 \]
$~~~~ ~~~~$ 代入

\[i^2=-1 \]
\[z_1\times z_2=ax+(ay+bx)i-by\\ =(ax-by)+(ay+bx)i \]
$~~~~ ~~~~$ 所以 $z_0$ 的向量可以表示为 $(ax-by,ay+bx)$ 。

$~~~~ ~~~~$ 如果两个复数互为共轭复数，则 $z\times \overline z=(a+bi)\times (a-bi)=a^2+b^2$ ，而这肯定是一个实数。

$~~~~ ~~~~$ 7.2 复平面上乘法： 设 $z_0=z_1\times z_2$ ，$z_0,z_1,z_2$ 的幅角分别是 $\theta_0,\theta_1,\theta_2$ 。则 $\theta_0=\theta_1+\theta_2$ 。

$~~~~ ~~~~$ $\mathcal{Proof.}$

$~~~~ ~~~~$ 首先：

\[\theta_1=\arctan \dfrac{b}{a}\ \ \ \ \theta_2=\arctan \dfrac{y}{x}\ \ \ \ \theta_0=\arctan \dfrac{ay+bx}{ax-by} \]
$~~~~ ~~~~$ 由反正切的加法：

\[\arctan \alpha \pm \arctan \beta=\arctan \dfrac{\alpha\pm \beta}{1 \mp \alpha \beta} \]
$~~~~ ~~~~$ 至于为什么其实类比一下 $\tan(\alpha+\beta)$ 就好了。

$~~~~ ~~~~$ 所以：

\[\arctan \dfrac{b}{a}+\arctan \dfrac{y}{x} =\arctan \dfrac{\dfrac{b}{a}+\dfrac{y}{x}}{1-\dfrac{b}{a}\times \dfrac{y}{x}}=\arctan \dfrac{ay+bx}{ax-by}=\theta_0 \]
$~~~~ ~~~~$ $\mathcal{Q.E.D}$

$~~~~ ~~~~$ 而模长的关系为 $|z_0|=|z_1|\times |z_2|$ 。这个仿照上面去证就好了。
$~~~~$ 8.复数的指数幂

$~~~~$ 由欧拉公式：

\[e^{i\theta}=\cos \theta+i \sin \theta \]
$~~~~$ 所以当 $\theta=\pi$ 时：

\[e^{i\pi}=\cos \pi+i \sin \pi=-1 \]
$~~~~$ 9.单位根

$~~~~$ 下文的 $n$ 均为 $2$ 的正整数幂，即满足 $n=2^k,k\in \text N^*$ 。

$~~~~ ~~~~$ 9.1 代数定义 在 $C$ （复数域）下，满足 $x^n=1$ 的 $x$ 被称为 $n$ 次单位根，而由代数基本定理，$n$ 次单位根共 $n$ 个。

$~~~~ ~~~~$ 9.2 复平面上定义 ：在复平面上，以原点为圆心，$1$ 为半径作单位圆。以原点为起点，单位圆的 $n$ 等分点为终点作 $n$ 个向量且其中一个向量表示的数为 $1$ 的所有向量表示的复数。

$~~~~ ~~~~$ 9.3 本原单位根 在 $n$ 次单位根中，设幅角为正且最小的一个为 $\omega_n$ ，则 $\omega_n$ 为 $n$ 次本原单位根。

$~~~~ ~~~~$ 9.4 单位圆上的向量： 若我们在单位圆上有一个幅角为 $\theta$ 的向量，那么这个向量的终点坐标为 $(\cos \theta,\sin \theta)$ 。

$~~~~ ~~~~$ 9.4 单位根的值： 由上可知，在 $n$ 次单位根中，除本原单位根外其余 $n-1$ 个单位根分别是 $\omega_n^2,\omega_n^3,\dots,\omega_n^n$ （幅角叠加，模长始终为 $1$ ），需要注意的是 $\omega_n^n=1$ 。

$~~~~$ 若想计算 $n$ 次单位根的值，肯定要先算出本原单位根。显然 $n$ 次本原单位根的幅角为 $\dfrac{2\pi}{n}$ ，那么 $n$ 次本原单位根的终点坐标为 $(\cos \dfrac{2\pi}{n},\sin \dfrac{2\pi}{n})$ ，它表示的值就是 $\cos \dfrac{2\pi}{n}+i\times \sin \dfrac{2\pi}{n}$ 。而根据欧拉公式，它可以被记为 $e^{i \frac{2\pi}{n}}$ ，故任意 $n$ 次单位根的值 $\omega_n^k=e^{ik\frac{2\pi}{n}}$ 。

$~~~~ ~~~~$ 9.5 单位根的性质：

$~~~~ ~~~~ ~~~~$ 9.5.1： $\omega_{an}^{ak}=\omega_n^k$ 。证明：代入求值的公式，发现 $a$ 可以约掉。或者从几何的角度来看，$n$ 等分单位圆的第 $k$ 个点就是 $an$ 等分单位圆的第 $ak$ 个点。

$~~~~ ~~~~ ~~~~$ 9.5.2： $\omega_n^{k+\frac{n}{2}}=-\omega_n^{\frac{n}{2}}$ 。证明：代入求值公式。或者从几何的角度来看，这就相当于单位圆的 $n$ 等分点的第 $k$ 个多绕半周单位圆，此时它们表示的值互为相反数。

二、快速傅里叶变换

$~~~~$ 还记得上面的多项式乘法吗，我们来分析它们的时间复杂度。

$~~~~$ 若用系数表示法，则两式依次相乘为 $\mathcal{O(n^2)}$ 。

$~~~~$ 若用点值表示法，则选点需要 $\mathcal{O(n^2)}$ （称为求值），还原回系数表示法需要 $\mathcal{O(n^3)}$ （称为插值）。

$~~~~$ 因此下面优将分别优化求值和插值。

快速傅里叶变换（FFT）

$~~~~$ 考虑一个 $n$ 项，$n-1$ 次的多项式 $A(x)=\sum_{i=0}^{n-1} a_i\times x^i$ 。

$~~~~$ 将它转化为点值表示，一种方法是我们分别带 $n$ 次单位根进去，但这样是 $n^2$ 的。

$~~~~$ 现在将它的各个单项式按次数分为奇次和偶次：

\[\large A(x)=\sum_{i=0}^{\frac{n}{2}-1} a_{2i}\times x^{2i}+\sum_{i=0}^{\frac{n}{2}-1} a_{2i+1}\times x^{2i+1}\\ \large =\sum _{i=0}^{\frac n 2-1}a_{2i}\times (x^2)^i+\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}\times x\times (x^2)^i \]
$~~~~$ 令：$A_0(x),A_1(x)$ 为两个 $(\frac{n}{2}-1)$ 次多项式，满足：

\[A_0(x)=\sum_{i=0}^{\frac{n}2-1}a_{2i}\times x^i\ \ ， \ \ A_1(x)=\sum_{i=0}^{\frac n 2-1}a_{2i+1}\times x^i \]
$~~~~ $则 $A(x)=A_0(x^2)+x\times A_1(x^2)$ 。

$~~~~$ 所以，我们的问题变成计算 $A_0(x^2)$ 和 $A_1(x^2)$ 的点值，这样可以达到 $\mathcal O(n)$ 计算 $A(x)$ 。

$~~~~$ 此时我们尝试带一个 $n$ 次单位根 $\omega_n^k$ ：

\[\large A(\omega_n^k)=A_0(\omega_n^{2k})+\omega_n^{k}\times A_1(\omega_n^{2k}) \\ \large =A_0(\omega_{\frac{n}{2}}^k)+\omega_{n}^k\times A_1(\omega_{\frac{n}{2}}^k) ......一.9.5.1 \]
$~~~~$ 那顺手再用一下第二个性质（一.9.5.2），代入 $\omega_n^{k+\frac{n}{2}}$

\[\large A(\omega_{n}^{k+\frac{n}{2}}) =A_0((-\omega_n^k)^2)+(-\omega_n^k)\times A_1((-\omega_n^k)^2) \\ \large =A_0(\omega_n^{2k})-\omega_n^{k}\times A_1(\omega_n^{2k}) \]
$~~~~$ 你似乎发现了，代入 $\omega_n^k$ 与 $\omega_n^{k+\frac{n}{2}}$ 只会造成 $A_1$ 的系数符号不同。

$~~~~$ 那这意味着我们在第一个式子依次取 $\omega_n^k,k\in [0,\frac n 2-1]$ 时，第二个式子可以马上帮我们算出取 $\omega_n^k,k\in [\frac n 2,n-1]$ 时的点值。

$~~~~$ 也就是说我们可以每次缩小问题规模为原来的一半，直到只剩下常数项。

$~~~~$ 那么时间复杂度由于问题规模每次缩小为原来一半，类比线段树，为 $\mathcal O(n \log n)$ 。

离散傅里叶逆变换（IDFT）

$~~~~$ 上面的过程最后你得到的其实是点值表示法的多项式，所以你必须把它还原为系数表示法。

$~~~~$ 设：数列 $\{b_i\}$ 表示一个 $(n-1)$ 次多项式进行 FFT 后得到的点值，即：

\[b_k=\sum_{i=0}^{n-1}a_i\times \omega_n^{ik} \]
$~~~~$ 这里直接给一个结论：

\[a_k=\dfrac{1}{n}\sum_{i=0}^{n-1}b_i \times \omega_n^{-ik} \]
$~~~~$ ~~（你发现这东西跟上面的式子非常相似）~~

$~~~~$ $\mathcal{Proof.}$

$~~~~$ 设有另一数列 $\{c_i\}$ ，满足：

\[c_k=\sum_{i=0}^{n-1}\pmb {b_i}\times \omega_n^{-ik} \]
$~~~~$ 注意是 $b_i$，因为我们是根据 $b$ 来推 $a$ ，也就是化成跟上面类似的形式。

\[\large c_k=\sum_{i=0}^{n-1}b_i\times \omega_{n}^{-ik}\\ \large =\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j\times \omega_n^{ij})\times\omega_n^{-ik} \dots（\text{展开}b_i）\\ \large =\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j\times \omega_{n}^{ij}\times \omega_n^{-ik})\\ \large =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j\times \omega_{n}^{ij}\times \omega_n^{-ik}\\ \large =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j\times \omega_n^{i\times(j-k)}\\ \large =\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j\times (\omega_n^{j-k})^i \\ \large =\sum_{j=0}^{n-1} a_j\times(\sum_{i=0}^{n-1}(\omega_n^{j-k})^i) \]
$~~~~$ 考虑怎么算后面一坨。

$~~~~$ 设等比数列求和 $S(x)=\sum_{i=0}^{n-1} x^i$ ，将 $\omega_n^k$ 代入：

\[\large S(\omega_{n}^k)=\sum_{i=0}^{n-1} (\omega_{n}^k)^i ......①\\ \large \omega_n^k\times S(\omega_{n}^k)=\sum_{i=1}^n (\omega_n^k)^i......②\\ \large \Rightarrow S(\omega_{n}^k)=\dfrac{②-①}{\omega_n^k-1}=\dfrac{\omega_n^{nk}-1}{\omega_n^k-1}=\dfrac{(\omega_n^n)^k-1}{\omega_n^k-1}=\dfrac{0}{\omega_n^k-1} \]
$~~~~$ $k<n$ ，分两种情况讨论：

$~~~~ ~~~~$ 当 $k\not=0$ 时，原式为 $0$ ；

$~~~~ ~~~~$ 当 $k=0$ 时，直接代入 $S(\omega_n^0)=S(1)=n$ 。

$~~~~$ 好，返回上面的那个式子

\[\large =\sum_{j=0}^{n-1} a_j\times(S(\omega_n^{j-k})) \]
$~~~~ ~~~~$ 当 $j\not = k$ 时，$\sum$ 后面一坨是 $0$ ；

$~~~~ ~~~~$ 当 $j=k$ 时，$\sum$ 后面一坨是 $n$ 。

\[\large c_k=na_k\\ \large a_k=\dfrac{c_k}n\\ \]
$~~~~$ 再代入 $c_k$ :

\[\large a_k=\dfrac{\sum_{i=0}^{n-1}b_i\times \omega_n^{-ik}}{n}\\ \large =\dfrac{1}{n}\times \sum_{i=0}^{n-1}b_i\times (\omega_n^{-k})^i \]
$~~~~$ $\mathcal{Q.E.D}$.

快速傅里叶逆变换（IFFT）

$~~~~$ 上面的式子当然不代也没什么事，毕竟我们只需要 $\sf{FFT}$ 求出 $\{c_i\}$ 即可。

$~~~~$ 具体来说，$\omega_n^{-ik}=\omega_n^{-ik+n}$ （两次 一.9.5.2）

$~~~~$ 所以

\[\large c_k=\sum_{i=0}^{n-1}b_i\times (\omega_n^{n-k})^i \]
$~~~~$ 我们先求出 $c_k$ 本身在 $b_i$ 下的点值，然后把 $c[1,n]$ （注意不是 $c[0,n]$ ，因为 $\omega_n^0=\omega_n^n=1$）倒置一下就好了。

$~~~~$ 然后你就做到了 $\mathcal O(n \log n)$ 计算多项式乘法。

FFT的优化 ——迭代实现

$~~~~$ 你发现原序列为 $[0,7]$ 的上升序列，而之后的序列为原序列每个二进制数的逆序。

$~~~~$ 所以提前逆序一下二进制数，可以避免递归。然后向上合并即可。

代码
查看代码

#include <cmath> #include <cstdio> #include <algorithm> using namespace std; int n,m,Lg=0; const double PI=acos(-1); struct Complex{ double r,i; Complex(){} Complex(double R,double I){r=R,i=I;} Complex operator +(Complex &x){return Complex(r+x.r,i+x.i);} Complex operator -(Complex &x){return Complex(r-x.r,i-x.i);} Complex operator *(Complex &x){return Complex(r*x.r-i*x.i,r*x.i+i*x.r);} void operator +=(Complex &x){r+=x.r,i+=x.i;} void operator *=(Complex &x){double tmp=r;r=r*x.r-i*x.i,i=tmp*x.i+i*x.r;} }F[10000005],G[10000005],H[10000005]; int To[10000005]; void Swap(Complex &a,Complex &b){Complex t=a;a=b;b=t;} void FFT(Complex *A,int op) { for(int i=0;i<n;i++) if(i<To[i]) Swap(A[To[i]],A[i]); for(int i=1;i<n;i<<=1)// i=每层子问题/2 { Complex W=Complex(cos(PI/i),sin(PI/i)*op); // 本原单位根 \omega_i for(int j=0;j<n;j+=i<<1) { Complex w=Complex(1,0); for(int k=0;k<i;k++,w*=W) { Complex x=A[j+k],y=w*A[i+j+k]; A[j+k]=x+y;A[i+j+k]=x-y; } } } } double Fabs(double x){return x>0?x:-x;} int main() { scanf("%d %d",&n,&m); for(int i=0;i<=n;i++) scanf("%lf",&F[i].r); for(int i=0;i<=m;i++) scanf("%lf",&G[i].r); for(m+=n,n=1;n<=m;n<<=1,Lg++); for(int i=0;i<n;i++) To[i]=(To[i>>1]>>1)|((i&1)<<(Lg-1)); FFT(F,1);FFT(G,1); for(int i=0;i<n;i++) H[i]=F[i]*G[i]; FFT(H,-1); for(int i=0;i<=m;i++) printf("%.0f ",Fabs(H[i].r)/n); return 0; }
参考资料

快速傅里叶变换(FFT)详解————自为风月马前卒

题解P3803 【模板】多项式乘法(FFT)————一扶苏一

三、快速数论变换

$~~~~$ $\sf{FFT}$ 是挺好，但它涉及到了实数运算，因此掉精度（残缺的字符串）和无法取模都是它的问题。换句话说如果你的多项式系数都很大，那你就没办法了。

$~~~~$ 因此我们考虑用什么东西来替换单位根，那么就要知道替换的东西要满足哪些性质。

$~~~~$ 来看单位根的性质：
1. 所有 $\omega_n^k(0\leq k\leq n-1)$ 互不相同：保证带进去时点的坐标不同。
2. $\omega_{an}^{ak}=\omega_{n}^k$ ：$\sf FFT$ 使用的性质，可以参见上面。
3. $\omega_n^{k+\frac{n}{2}}=-\omega_n^{\frac{n}{2}}$ ：$\sf FFT$ 使用的性质，可以参见上面。
4. $\sum_{i=0}^{n-1} \omega_n^{ki}$ 在 $k \not =0$ 时值为 $0$ ，在 $k=0$ 时值为 $n$ ：$\sf IFFT$ 使用的性质，可以参见上面。
$~~~~$ 综合上面的性质，我们可以使用原根来替代单位根 。

原根及其性质

$~~~~$ 考虑一个质数 $p=nq+1$ 。$n$ 为 $2$ 的幂。则 $p$ 的原根 $g$ 为使得 $g^i(0\leq i\leq \varphi(p)=p-1)$ 互不相同的一个正整数。由定义可得，一个数的原根可能有很多个。

$~~~~$ 由于定义，这些性质原根也是可以满足的。

求一个数的原根

$~~~~$ 我们使用枚举法，即依次枚举一个数，判断其是否是 $p$ 的原根。一般来说，质数的原根都很小。

$~~~~$ 而检验时，我们使用如下的性质：

$~~~~ ~~~~$ 对于一个数 $g$ ，最小的满足 $g^k \equiv 1 \pmod p$ 的正整数 $k$ 一定是 $p-1$ 的约数。

$~~~~$ 故如果我们在 $p-1$ 的所有约数中找不到一个 $q$ 满足 $g^q\equiv 1\pmod p$ ，就说明这是原根。

代码
查看代码

bool check(ll gg,ll x) { for(int i=2;i*i<=x-1;i++) { if((x-1)%i==0&&(qpow(gg,i,x)==1||qpow(gg,(x-1)/i,x)==1)) return false; } return true; } void GetG(ll x) { ll ret=0; for(ll i=2;i<x;i++) if(check(i,x)){ret=i;break;} }
NTT

$~~~~$ 我们只需要把原来 $\sf FFT$ 中所有的 $\omega_n$ 改为 $g^q$ 即可。但注意除法需要改为求逆元。

代码
查看代码

const int MOD=998244353,g=3,gi=332748118; ll qpow(ll a,ll b) { ll ret=1; while(b) { if(b&1) ret=ret*a%MOD; a=a*a%MOD;b>>=1; } return ret; } void NTT(ll *S,int op) { for(int i=0;i<n;i++) if(i<To[i]) swap(S[i],S[To[i]]); for(int i=1;i<n;i<<=1) { ll W=qpow(op==1?g:gi,(MOD-1)/(i<<1)); for(int j=0;j<n;j+=i<<1) { ll w=1; for(int k=0;k<i;k++,w=w*W%MOD) { ll x=S[j+k],y=w*S[i+j+k]%MOD; S[j+k]=(x+y)%MOD;S[i+j+k]=(x-y)%MOD; } } } if(op==-1) { ll Inv=qpow(n,MOD-2); for(int i=0;i<N;i++) S[i]=S[i]*Inv%MOD; } }
参考资料

从傅里叶变换到数论变换——Menci

四、三模NTT/MTT

咕，咕咕咕 ~~（拟声）~~

五、多项式求逆

$~~~~$ 多项式做除法的话，就必须像普通数在取余的情况下做除法一样求得逆元。

$~~~~$ ~~一般这东西朗读并背诵全文就行了。~~

本部分的一小点前置知识

$~~~~$ 多项式的度数： 多项式最高次项的次数（或者说就是多项式的次数），多项式 $A(x)$ 的度为 $deg_A$ 。

$~~~~$ 多项式的带余除法： 设有多项式 $A(x),B(x)$ ，则存在唯一的 $Q(x),R(x)$ 满足 $A(x)=B(x)Q(x)+R(x)$ ，且 $deg_R<deg_B$ 称 $Q(x)$ 为商,$R(x)$ 为余数。同时有：

\[A(x)\equiv R(x) \pmod {B(x)} \]
$~~~~$ 多项式的逆元： 若存在多项式 $B(x)$ ，满足 $A(x) \times B(x) \equiv 1 \pmod{x^n}$ ，则称 $B(x)$ 为 $A(x)$ 的逆元，记作 $A^{-1}(x)$ 。后面的模数 $x^n$ 其实相当于舍弃掉乘积在 $x^{n+1}$ 及以后的所有系数。

如何求逆元

$~~~~$ 假设我们现在求到了 $A(x)$ 在 $\bmod x^{\lceil \frac{n}{2} \rceil}$ 下的逆元 $B'(x)$ ，现在想求 $B(x)=A^{-1}(x)$ 。

$~~~~$ 因此有：

\[A * B'\equiv 1\pmod {x^{\lceil \frac{n}2\rceil}}\\ \]
$~~~~$ 显然，一个在更广泛的模意义下的逆元乘起来它的系数从低到高依然是 $1,0,0,0,0,\dots$ ，因此有：

\[A * B \equiv 1 \pmod{x^{\lceil \frac{n}2\rceil}} \]
$~~~~$ 下 $-$ 上：

\[A*(B-B')\equiv 0 \pmod{x^{\lceil \frac{n}2\rceil}} \]
$~~~~$ 显然 $A \bmod x^{\lceil \frac{n}2\rceil}$ 不为 $0$ ，故 $B-B' \bmod x^{\lceil \frac{n}2\rceil}=0$

$~~~~$ 因此：

\[B-B' \equiv 0 \pmod{x^{\lceil \frac{n}2\rceil}} \]
$~~~~$ 考虑如何上升到 $x^n$ ，很难不难想到进行平方：

\[(B-B')^2 \equiv 0 \pmod{x^n} \]
$~~~~$ $\mathcal{Proof.}$

$~~~~$ 设平方后的多项式为 $F(x)$ ，系数序列为 $b_i$

$~~~~$ 对于 $i=0$ ，显然跟之前一样，即 $b_i=1$ 。

$~~~~$ 对于 $1\leq i \leq \lceil \dfrac{n}{2} \rceil$ :由于原来其本身和次数小于它的所有非常数项的系数是 $0$ ，卷积后肯定也是 $0$ 。

$~~~~$ 对于 $\lceil \dfrac{n}{2} \rceil < i \leq n$ ，$b_i=\sum_{j=0}^i a_j\times a_{i-j}$ ，而由于原先的 $0$ 是过半的，因此不论 $j$ 取什么值，都有，各加数都为 $0$ 。

$~~~~$ 综上，对于 $i=0$ ，$b_i=1$ ；否则：$b_i=0$ 。

$~~~~$ $\mathcal{Q.E.D.}$

$~~~~$ 展开平方：

\[B^2 -2B*B'+B'^2 \equiv 0 \pmod{x^n} \]
$~~~~$ 然而如果直接把 $B^2$ 甩过去，会出现多项式开根~~，而多项式开根又需要多项式求逆，所以这两个东西都不可做~~ ，所以我们两边同时卷上 $A$ ：

\[AB^2-2AB*B'+AB'^2 \equiv 0\pmod{x^n} \]
$~~~~$ 而 $AB\equiv 1\pmod{x^n}$：

\[B -2B'+AB' \equiv 0 \pmod{x^n}\\ B \equiv 2B'-AB' \pmod{x^n} \]
$~~~~$ 每层递归计算就行了，出口就是多项式只剩下常数项时，这时就是普通的求逆元了。

代码
查看代码

#include <cstdio> #include <algorithm> #define ll long long using namespace std; int To[1000005],N; const ll MOD=998244353; ll qpow(ll a,ll b) {......}//快速幂 const int g=3,gi=qpow(g,MOD-2); void NTT(ll *S,int op)//NTT { ...... if(op==-1) { ll Inv=qpow(N,MOD-2); for(int i=0;i<N;i++) S[i]=S[i]*Inv%MOD; } } int n; ll F[1000005],G[1000005],C[1000005]; void GetInv(int deg,ll *A,ll *B) { if(deg==1){B[0]=qpow(A[0],MOD-2);return;} GetInv((deg+1)>>1,A,B); for(N=1;N<=(deg<<1);N<<=1); for(int i=0;i<N;i++) To[i]=(To[i>>1]>>1)|((i&1)*(N>>1)),C[i]=A[i]; for(int i=deg;i<N;i++) C[i]=0; NTT(C,1);NTT(B,1); for(int i=0;i<N;i++) B[i]=B[i]*(((2ll-B[i]*C[i]%MOD)+MOD)%MOD)%MOD; NTT(B,-1); for(int i=deg;i<N;i++) B[i]=0; } int main() { scanf("%d",&n); for(int i=0;i<n;i++) scanf("%lld",&F[i]); GetInv(n,F,G); for(int i=0;i<n;i++) printf("%lld ",G[i]); return 0; }
六、多项式开根

$~~~~$ 上面是不是提到了多项式开根？

$~~~~$ 求多项式 $g(x)$ 使得 $g^2(x)\equiv f(x) \pmod {x^n}$ 即多项式开根。

$~~~~$ 一般情况下，被开方的多项式常数项为完全平方数。（否则就没法直接 $\sf NTT$ 做了）

求解过程

$~~~~$ 跟求逆差不多，我们假设 $g^2_0(x) \equiv f(x) \pmod{2^{\lceil \frac x 2 \rceil}}$ ，即上一层的解。

$~~~~$ 那么：

\[g_0 \equiv \sqrt f \pmod{2^{\lceil \frac x 2 \rceil}}\\ g_0^2 \equiv f \pmod {2^{\lceil \frac x 2 \rceil}}\\ g_0^2-f \equiv 0 \pmod {2^{\lceil \frac x 2 \rceil}}\\ \]
$~~~~$ 继续沿用上面的套路，两边平方，具体证明见上。

\[(g_0^2-f)^2 \equiv 0 \pmod{2^n}\\ \]
$~~~~$ 进行一个变形：

\[(g_0^2 +f)^2 \equiv 4g_0^2*f \pmod{2^n}\\ \dfrac{(g_0^2+f)^2}{4 g_0^2}\equiv f \pmod{2^n}\\ \]
$~~~~$ 两边开根：

\[\dfrac{g_0^2+f}{2 g_0} \equiv g \pmod{2^n} \]
$~~~~$ 然后我们就得到了 $g$ 的式子。

$~~~~$ 具体实现的时候仍然递归，但由于每层还要求逆，所以时间复杂度为 $\mathcal{O(n \log^2 n)}$ 。

代码

不知道为什么，我的代码不开O2 过洛谷模板，9s多，开了 3s多。

所以仅供参考。具体实现方式还有开根时每层循环来迭代的，可能会快一些。
查看代码

#include <cstdio> #include <algorithm> #define ll long long using namespace std; const ll MOD=998244353; ll To[5000005],N; ll qpow(ll a,ll b){...}//快速幂 const ll g=3,gi=qpow(g,MOD-2); const ll Inv2=qpow(2,MOD-2); inline ll Add(ll a,ll b){return ((a+b)%MOD+MOD)%MOD;} inline ll Mul(ll a,ll b){return a*b%MOD;} void NTT(ll *S,ll op){...}//多项式乘法 ll C[5000005]; void GetInv(int deg,ll *A,ll *B){...}//求逆元 ll inv[5000005],D[5000005];//注意新开数组存 void GetSqrt(int deg,ll *A,ll *B) { if(deg==1){B[0]=1;return;} GetSqrt((deg+1)>>1,A,B); for(N=1;N<=(deg<<1);N<<=1); for(int i=0;i<N;i++) To[i]=(To[i>>1]>>1)|((i&1)*(N>>1)),D[i]=inv[i]=0; for(int i=0;i<deg;i++) D[i]=A[i]; GetInv(deg,B,inv); NTT(inv,1);NTT(D,1);NTT(B,1); for(int i=0;i<N;i++) B[i]=Mul(Add(B[i],Mul(D[i],inv[i])),Inv2); NTT(B,-1); for(int i=deg;i<N;i++) B[i]=0; } ll F[5000005],G[5000005]; int main() { int n;read(n); for(int i=0;i<n;i++) scanf("%lld",&F[i]); GetSqrt(n,F,G); for(int i=0;i<n;i++) printf("%lld ",G[i]); return 0; }
七、多项式除法

$~~~~$ 一般说的多项式除法指带余除法，即给定多项式 $F(x),G(x)$ ，求 $Q(x),R(x)$ 满足 $F(x)=G(x)*Q(x)+R(x)$ ，其中 $deg_R<deg_G$ 。

$~~~~$ ~~这个东西其实一般也是朗读并全文背诵。~~

$~~~~$ 顺便提一下，一般人工做这个东西的时候都是用大除法。

求解过程

$~~~~$ 由上面的定义，我们知道：

\[F(x)=G(x)*Q(x)+R(x) \]
$~~~~$ 显然更换代入的 $x$ 上式仍然成立：

\[F(\dfrac{1}{x})=G(\dfrac{1}{x})*Q(\dfrac{1}{x})+R(\dfrac{1}{x}) \]
$~~~~$ 设： $deg_F=n,deg_G=m$，两边同时乘上 $x^n$ ：

\[x^nF(\dfrac{1}{x})=x^nG(\dfrac{1}{x})*Q(\dfrac{1}{x})+x^nR(\dfrac{1}{x}) \]
$~~~~$ 我们发现一件事：$x^n\times \sum_{i=0}^{n} a_i\times \dfrac{1}{x^i}=\sum_{i=0}^n a_{n-i}x^i$ ，即得到了原来的多项式系数序列翻转后的多项式。

$~~~~$ 把上面的式子都拆一下，不难确认：$deg_Q=n-m,deg_R<m$ ，因此：

\[x^nF(\dfrac{1}{x})=x^mG(\dfrac{1}{x})*x^{n-m}Q(\dfrac{1}{x})+x^{m-1}R(\dfrac{1}{x})\times x^{n-m+1} \]
$~~~~$ 记 $x^n\times F(\dfrac{1}{x})$ 为 $F_R(x)$ ，表示翻转后的 $F(x)$ ，则：

\[F_R(x)=G_R(x)*Q_R(x)+R_R(x)\times x^{n-m+1} \]
$~~~~$ 来思考一个问题，我们为什么要这么拆？想到原来为什么不可做的原因就是 $R(x)$ 无法确定。

$~~~~$ 而现在，$R_R(x)$ 乘上了一个 $x^{n-m+1}$ ，可以借此消掉它：

\[F_R(x) \equiv G_R(x)*Q_R(x)+R_R(x)\times x^{n-m+1} \pmod {x^{n-m+1}}\\ F_R(x) \equiv G_R(x)*Q_R(x) \pmod {x^{n-m+1}} \]
$~~~~$ 所以：

\[Q_R(x) \equiv \dfrac{F_R(x)}{G_R(x)} \pmod {x^{n-m+1}} \]
$~~~~$ 显然，$n-m=deg_{G_R}< n-m+1$ 所以这是没有影响的，直接对 $G_R(x)$ 求逆元即可。

$~~~~$ 最后，$R(x)=F(x)-G(x)*Q(x)$ ，直接求即可。

代码

这题细节挺多的，稍不注意就会打挂，这里代码放完整版，个人错过的点注释在下面了。
查看代码

#include <cstdio> #include <algorithm> #define ll long long using namespace std; int N,To[4000005]; const ll MOD=998244353; inline ll Add(ll a,ll b){return (((a+b)%MOD)+MOD)%MOD;} inline ll Mul(ll a,ll b){return a*b%MOD;} ll qpow(ll a,ll b) { ll ret=1; while(b) { if(b&1) ret=Mul(ret,a); b>>=1;a=Mul(a,a); } return ret; } const ll gg=3,ggi=qpow(gg,MOD-2); void NTT(ll *S,ll op) { for(int i=0;i<N;i++) if(i<To[i]) swap(S[i],S[To[i]]); for(int i=1;i<N;i<<=1) { ll W=qpow(op==1?gg:ggi,(MOD-1)/(i<<1)); for(int j=0;j<N;j+=i<<1) { ll w=1; for(int k=0;k<i;k++,w=Mul(w,W)) { ll x=S[j+k],y=Mul(S[i+j+k],w); S[j+k]=Add(x,y);S[i+j+k]=Add(x,-y); } } } if(op==-1) { ll Inv=qpow(N,MOD-2); for(int i=0;i<N;i++) S[i]=Mul(S[i],Inv); } } ll C[4000005],A1[4000005],A2[4000005]; void mul(ll *A,ll *B,ll n,ll m) { for(N=1;N<=n+m;N<<=1); for(int i=0;i<N;i++) To[i]=(To[i>>1]>>1)|((i&1)*(N>>1)); for(ll i=0;i<N;i++) A1[i]=A[i],A2[i]=B[i]; NTT(A1,1);NTT(A2,1); for(ll i=0;i<N;i++) A[i]=Mul(A1[i],A2[i]); NTT(A,-1); } void GetInv(int deg,ll *A,ll *B) { if(deg==1){B[0]=qpow(A[0],MOD-2);return;} GetInv((deg+1)>>1,A,B); for(N=1;N<=(deg<<1);N<<=1); for(int i=0;i<N;i++) To[i]=(To[i>>1]>>1)|((i&1)*(N>>1)),C[i]=A[i]; for(int i=deg;i<N;i++) C[i]=0; NTT(C,1);NTT(B,1); for(int i=0;i<N;i++) B[i]=Mul(Add(2ll,-Mul(C[i],B[i])),B[i]); NTT(B,-1); for(int i=deg;i<N;i++) B[i]=0; } ll f[4000005],g[4000005],q[4000005],inv[4000005]; void Div(int n,int m,ll *F,ll *G,ll *Q) { for(int i=0;i<n;i++) Q[i]=F[i]; for(int i=0;i<m;i++) g[i]=G[i]; reverse(Q,Q+n);reverse(g,g+m); for(int i=n-m+1;i<m;i++) g[i]=0; GetInv(n-m+1,g,inv);//注意即使g只有m次，这里求在mod x^{n-m+1} 意义下的逆元。 mul(Q,inv,n,n-m+1);//最好封装一下乘法，不然很容易挂 reverse(Q,Q+n-m+1); for(int i=n-m+1;i<=N;i++) Q[i]=0; for(int i=0;i<=N;i++) inv[i]=0; } void Rest(int n,int m,ll *F,ll *G,ll *Q,ll *R) { for(int i=0;i<n;i++) f[i]=F[i]; for(int i=0;i<m;i++) g[i]=G[i]; for(int i=0;i<n-m+1;i++) q[i]=Q[i]; mul(g,q,m,n-m+1); for(int i=0;i<m-1;i++) R[i]=Add(f[i],-g[i]);//这里最后多项式加减直接对应系数加减就好了 } ll F[4000005],G[4000005],Q[4000005],R[4000005]; int main() { int n,m;scanf("%d %d",&n,&m);n++;m++; for(int i=0;i<n;i++) scanf("%lld",&F[i]); for(int i=0;i<m;i++) scanf("%lld",&G[i]); Div(n,m,F,G,Q); for(int i=0;i<n-m+1;i++) printf("%lld ",Q[i]);puts(""); Rest(n,m,F,G,Q,R); for(int i=0;i<m-1;i++) printf("%lld ",R[i]); return 0; }
来自 2021/08/23 的吐槽：果然忘完了，回来一看不仅没填坑而且还一堆错，为让之前的各位读者或许在某些地方感到困惑而致歉。

2021/08/26 的更新

八、多项式对数函数（多项式 ln）

$~~~~$ 求对数函数啊~

前置芝士

$~~~~$ 多项式求导：$f(x)$ 的导函数记为 $f'(x)$

$~~~~$ 对于函数 $f(x)=x^a$，有 $f'(x)=ax^{a-1}$。

$~~~~$ 对于函数 $f(x)=g(x)+h(x)$，有 $f'(x)=g'(x)+h'(x)$。

$~~~~$ 对于复合函数， $f(g(x))'=f'(g(x))g'(x)$

$~~~~$ 对数函数的导函数： $\ln'(x)=\dfrac{1}{x}$。

$~~~~$ 多项式积分： $f(x)$ 的积分记为 $\int f(x) dx$

$~~~~$ 对于函数 $f(x)=x^a$，有 $\int f(x) dx=\dfrac{1}{a+1}x^{a+1}$。

$~~~~$ 对于函数 $f(x)=g(x)+h(x)$ ，有 $\int f(x) dx =\int g(x) dx+\int h(x) dx$。

$~~~~$ 由上述定义可以积分和求导互为逆运算。

求解过程

$~~~~$ 记 $G(x) \equiv \ln (F(x)) \pmod {x^n}$ ，则我们要求的即为 $G(x)$。

$~~~~$ 对右边求导： $\ln(F(x))'=ln'(F(x))F'(x)=\dfrac{F'(x)}{F(x)}$ ，故：

\[G'(x) \equiv \dfrac{F'(x)}{F(x)} \pmod{x^n} \]
$~~~~$ 那么求出 $F'(x)\times F^{-1}(x)$ 后再积分一下就是 $G(x)=\ln F(x)$ 了。

代码
查看代码

int A1[500005],A2[500005]; void mul(int *A,int *B,int n,int m) { for(N=1;N<=n+m;N<<=1); for(int i=0;i<N;i++) To[i]=(To[i>>1]>>1)|((i&1)*(N>>1)); for(int i=0;i<N;i++) A1[i]=A[i],A2[i]=B[i]; NTT(A1,1);NTT(A2,1); for(int i=0;i<N;i++) A[i]=Mul(A1[i],A2[i]),A1[i]=A2[i]=0; NTT(A,-1); } int C[500005]; void GetInv(int *A,int *B,int deg) { if(deg==1){B[0]=qpow(A[0],MOD-2);return;} GetInv(A,B,(deg+1)>>1); for(N=1;N<=(deg<<1);N<<=1); for(int i=0;i<N;i++) To[i]=(To[i>>1]>>1)|((i&1)*(N>>1)),C[i]=A[i]; for(int i=deg;i<N;i++) C[i]=0; NTT(C,1);NTT(B,1); for(int i=0;i<N;i++) B[i]=Mul(Add(2ll,-Mul(C[i],B[i])),B[i]); NTT(B,-1); for(int i=deg;i<N;i++) B[i]=0; } void GetDev(int *F,int *G,int deg) { for(int i=1;i<deg;i++) G[i-1]=1ll*F[i]*i%MOD; G[deg-1]=0; } void GetInvDev(int *F,int *G,int deg) { for(int i=1;i<deg;i++) G[i]=1ll*F[i-1]*qpow(i,MOD-2)%MOD; G[0]=0; } int a[500005],b[500005]; void GetLn(int *F,int *G,int deg) { GetDev(F,a,deg);GetInv(F,b,deg); mul(a,b,deg,deg); GetInvDev(a,G,deg); }
查看全文

相关阅读:
轻重搭配
 EF的优缺点
 使用bootstrap-select有时显示“Nothing selected”
IIS发布 HTTP 错误 500.21
js添加的元素无法触发click事件
 sql server查看表是否死锁
 sql server把一个库表的某个字段更新到另一张表的相同字段
 SQLSERVER排查CPU占用高的情况
 SQL server中如何按照某一字段中的分割符将记录拆成多条
 LINQ to Entities does not recognize the method 'System.DateTime AddDays(Double)' method, and this method cannot be translated into a store expression.

原文地址：https://www.cnblogs.com/Azazel/p/14508489.html

多项式学习笔记

多项式学习笔记

一、前置芝士知识

二、快速傅里叶变换

快速傅里叶变换（FFT）

离散傅里叶逆变换 （IDFT）

快速傅里叶逆变换 （IFFT）

FFT的优化 ——迭代实现

代码

参考资料

三、快速数论变换

原根及其性质

求一个数的原根

代码

NTT

代码

参考资料

四、三模NTT/MTT

五、多项式求逆

本部分的一小点前置知识

如何求逆元

代码

六、多项式开根

求解过程

代码

七、多项式除法

求解过程

代码

八、多项式对数函数（多项式 ln）

前置芝士

求解过程

代码

离散傅里叶逆变换（IDFT）

快速傅里叶逆变换（IFFT）