Description
Solution
我们考虑将问题一步步拆解
第一步求出(F_{S,i})表示一次旅行按位与的值为S，走了i步的方案数。
第二步答案是(F_{S,i})的二维重复卷积，记答案为(S_{S,i})，那么(F_{S,i} imes S_{T,j})能够贡献到(S_{S&T,i+j})。
上下两部分是两个问题，我们分开来看。
考虑第一步
设原矩阵为A
根据定义，$$F_{S,i}=sumlimits_{x&y=T}A^i_{x,y}$$
容易看出F是线性的，用题解的话来说，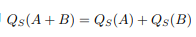
，并且内部的数乘可以移到外面
记(f(x))为矩阵A的特征多项式，它是个n次多项式，根据Cayley-Hamilton定理我们有(f(A)=0)
可以看出F只看i这一维的话就是一个n阶线性递推。
记(c)就是(x^i)对(f(x))取模的多项式系数。
我们有$$F_{S,i}=sumlimits_{x&y=T}sumlimits_{j=0}^{n-1}c_jA^{j}_{x,y}$$
这里(A^0)是单位矩阵，左对角线为1，因此对于任意S，(F_{S,0}=1)（当然在做完以后，我们是要去掉0的，因为不允许走0步）
交换主体$$F_{S,i}=sumlimits_{j=0}^{n-1}c_jsumlimits_{x&y=T}A^{j}_{x,y}$$
后面的东西就是(F_{S,j})
那么就有$$F_{S,i}=sumlimits_{j=0}^{n-1}c_jF_{S,j}$$
暴力出前n-1项的(F)，这是(O(n^4))的
求特征多项式有很多种方法就不赘述了， 一种比较好想的做法是带入n+1个值求行列式，然后高斯消元或者拉格朗日插值求出特征多项式，这也是(O(n^4))的（实际上可以(O(n^3))）。
多项式取模每次只会乘一个x，直接计算最高次项的影响，时间是(O(n))的
这样我们就在(O(n^4+mn^2))的时间复杂度内做完了前半部分。
考虑第二步的问题：
(F_{S,i})二维重复卷积，记答案为(S_{S,i})，那么(F_{S,i} imes S_{T,j})能够贡献到(S_{S&T,i+j})。
如果只有第二维，那很简单，直接就是(sum F(x)^i={1over 1-F(x)})，多项式求逆就好了。
但是我们现在有了第一维
考虑将第二维固定做一遍FWT的and卷积（就是枚举第二维i，看做一个一维的集合幂(F_i(S))）
那么现在所有的第一维and卷积都变成了点乘，
即原本(F_{S&T,i+j}+=F_{S,i} imes F_{T,j})
现在都变成了(F_{S,i+j}+=F_{S,i} imes F_{S,j})
我们发现这时再固定第一维（枚举每个S，把(F_S(x))看做一个独立的多项式），那么就变成了一维的普通幂级数重复拼接，套用多项式求逆即可。
这样我们就得到了第二维重复拼接的结果，它实际上同时进行了第一维的重复卷积。
此时按照一开始做FWT的时候固定第二维，逆FWT回去，就是最终的答案。
这一部分的复杂度是(O(mnlog m))的，常数比较大。
因此我们就在(O(mnlog m+n^4+mn^2))的时间复杂度解决了。
Code
（BZOJ被卡常了。。写的很丑）
#include <bits/stdc++.h>
#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fod(i,a,b) for(int i=a;i>=b;--i)
#define N 20005
#define T 70
#define M 65536
#define L 16
#define LL long long
#define mo 998244353
using namespace std;
int n,m;
LL a[T][M+1],ny[M+1],c[T][T];
LL ksm(LL k,LL n)
{
LL s=1;
for(;n;n>>=1,k=k*k%mo) if(n&1) s=s*k%mo;
return s;
}
//polynomial
LL ap[T][M+1],ans[T][M+1],cd[T],ct[T];
int n1;
namespace polynomial
{
LL wi[M+1],wg[M+1];
int bit[M+1],l2[M+1];
void prp(int num)
{
fo(i,0,num)
{
wi[i]=wg[i*(M/num)];
bit[i]=(bit[i>>1]>>1)|((i&1)<<(l2[num]-1));
}
}
void pre()
{
ny[1]=1;
fo(i,2,M) ny[i]=(-ny[mo%i]*(LL)(mo/i)%mo+mo)%mo;
fo(i,1,L) l2[1<<i]=i;
fod(i,M,2) if(!l2[i]) l2[i]=l2[i+1];
wg[0]=1,wg[1]=ksm(3,(mo-1)/M);
fo(i,2,M) wg[i]=wg[i-1]*wg[1]%mo;
}
void NTT(LL *a,bool pd,int num)
{
fo(i,0,num-1) if(i<bit[i]) swap(a[i],a[bit[i]]);
for(int m=2,h=1,l=num>>1;m<=num;h=m,m<<=1,l>>=1)
{
int c=(!pd)?l:-l;
for(int j=0;j<num;j+=m)
{
LL *x=a+j,*y=a+j+h,*w=(!pd)?wi:wi+num;
fo(i,0,h-1)
{
LL v=*y * *w%mo;
*y=(*x-v+mo)%mo;
*x=(*x+v)%mo;
x++,y++,w+=c;
}
}
}
if(pd) fo(i,0,num-1) a[i]=a[i]*ny[num]%mo;
}
void inv(int n,LL *a,LL *b)
{
static LL u1[M+1],u2[M+1];
b[0]=ksm(a[0],mo-2);
for(int m=1,t=2,num=4;m<n;m=t,t=num,num<<=1)
{
prp(num);
fo(i,0,num-1) u1[i]=u2[i]=0;
fo(i,0,m-1) u1[i]=b[i];
fo(i,0,t-1) u2[i]=a[i];
NTT(u1,0,num),NTT(u2,0,num);
fo(i,0,num-1) u1[i]=u1[i]*u1[i]%mo*u2[i]%mo;
NTT(u1,1,num);
fo(i,0,t-1) b[i]=((LL)2*b[i]-u1[i]+mo)%mo;
fo(i,t,num-1) b[i]=0;
}
}
void gmod()
{
LL v=ksm(cd[n1],mo-2)*ct[n1]%mo;
fo(i,0,n1) ct[i]=(ct[i]-v*cd[i]%mo+mo)%mo;
}
}
using namespace polynomial;
//matrix
LL c1[T][T],al[T][T];
namespace matrix
{
void ti()
{
static LL z[T][T];
memset(z,0,sizeof(z));
fo(i,0,n-1)
{
fo(k,0,n-1)
{
fo(j,0,n-1) z[i][j]=(z[i][j]+c1[i][k]*c[k][j])%mo;
}
}
fo(i,0,n-1) fo(j,0,n-1) c1[i][j]=z[i][j];
}
LL det(int k)
{
static LL z[T][T];
memcpy(z,c,sizeof(c));
fo(i,0,n-1) z[i][i]=(z[i][i]-k+mo)%mo;
LL v=1;
fo(i,0,n-1)
{
fo(k,i,n-1)
{
if(z[k][i])
{
if(k!=i) swap(z[k],z[i]),v=-v;
break;
}
}
if(!z[i][i]) return 0;
LL vn=ksm(z[i][i],mo-2);
fo(k,i+1,n-1)
{
if(z[k][i])
{
LL v=z[k][i]*vn%mo;
fo(j,i,n-1) z[k][j]=(z[k][j]-v*z[i][j])%mo;
}
}
}
fo(i,0,n-1) v=v*z[i][i]%mo;
return v;
}
void gauss()
{
fo(i,0,n)
{
fo(k,i,n)
{
if(al[k][i])
{
if(k!=i) swap(al[k],al[i]);
break;
}
}
if(!al[i][i]) continue;
LL v=ksm(al[i][i],mo-2)%mo;
fo(k,i,n+1) al[i][k]=al[i][k]*v%mo;
fo(k,i+1,n)
{
if(al[k][i])
{
v=al[k][i];
fo(j,i,n+1) al[k][j]=(al[k][j]-v*al[i][j])%mo;
}
}
}
fod(i,n,0)
{
if(al[i][i])
{
fod(k,i-1,0)
{
if(al[k][i])
{
LL v=al[k][i];
fo(j,i,n+1) al[k][j]=(al[k][j]-v*al[i][j])%mo;
}
}
}
}
}
}
using namespace matrix;
void FWT(int t,bool pd)
{
for(int m=2,h=1;m<=n;h=m,m<<=1)
for(int j=0;j<n;j+=m)
fo(i,0,h-1) a[i+j][t]=(a[i+j][t]+((!pd)?1:-1)*a[i+j+h][t]+mo)%mo;
}
int main()
{
cin>>n>>m;
pre();
fo(i,0,n-1)
fo(j,0,n-1)
scanf("%lld
",&c[i][j]),c1[i][j]=c[i][j];
fo(i,0,n)
{
LL v=i;
al[i][0]=1;
fo(j,1,n) al[i][j]=v,v=v*(LL)i%mo;
al[i][n+1]=det(i);
}
gauss();
fo(i,0,n) cd[i]=al[i][n+1];
n1=n;
fo(i,0,n-1) a[i][0]=1;
while(cd[n1]==0) n1--;
fo(i,1,n1-1)
{
fo(x,0,n1-1) fo(y,0,n-1) a[x&y][i]=(a[x&y][i]+c1[x][y])%mo;
ti();
}
ct[n1-1]=1;
fo(i,n1,m)
{
fod(j,n1,1) ct[j]=ct[j-1];
ct[0]=0;
gmod();
fo(x,0,n-1) fo(j,0,n1-1) a[x][i]=(a[x][i]+ct[j]*a[x][j]%mo+mo)%mo;
}
fo(i,0,n-1) a[i][0]=0;
memset(ap,0,sizeof(ap));
fo(j,1,m) FWT(j,0);
fo(i,0,n-1)
{
a[i][0]++;
fo(j,1,m) a[i][j]=-a[i][j];
inv(m+1,a[i],ap[i]);
}
fo(j,1,m)
{
fo(i,0,n-1) a[i][j]=ap[i][j];
FWT(j,1);
}
LL ans=0;
fo(i,0,n-1) fo(j,1,m) ans^=a[i][j];
printf("%lld
",ans);
}