洛谷题目链接:[HAOI2018]苹果树
题目背景
HAOI2018 Round2 第一题
题目描述
小 C 在自己家的花园里种了一棵苹果树, 树上每个结点都有恰好两个分支. 经过细心的观察, 小 C 发现每一天这棵树都会生长出一个新的结点.
第一天的时候, 果树会长出一个根结点, 以后每一天, 果树会随机选择一个当前树中没有长出过结点 的分支, 然后在这个分支上长出一个新结点, 新结点与分支所属的结点之间连接上一条边.
小 C 定义一棵果树的不便度为树上两两结点之间的距离之和, 两个结点之间 的距离定义为从一个点走到另一个点的路径经过的边数.
现在他非常好奇, 如果 (N) 天之后小 G 来他家摘苹果, 这个不便度的期望 (E) 是多少. 但是小 C 讨厌分数, 所以他只想知道 (E imes N !) 对 (P) 取模的结果, 可以证明这是一个整数.
输入输出格式
输入格式:
从标准输入中读入数据. 一行两个整数 (N), (P) .
输出格式:
输出到标准输出中. 输出一个整数表示答案.
输入输出样例
输入样例#1:
3 610745795
输出样例#1:
24
输入样例#2:
305 1000000007
输出样例#2:
865018107
说明
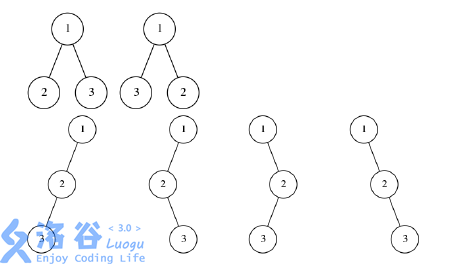
以上是所有 (N = 3) 时可能的苹果树形态, 其中编号表示这个结点是第几天生 长出来的, 显然每种情况两两结点的距离均为 (4) .
题解: 这个枚举方式比较神奇...我也不太清楚为什么可以做到不重不漏,有人会可以帮我分析一下...
直接讲方法吧:
首先考虑如何计算贡献,我们分每条边来计算贡献,那么总贡献就是(sum size*(n-size))
考虑当前枚举到了节点(i),它有一颗大小为(j)的子树,那么前(i)个节点可能组成的方案数是(i!),这个大小为(j)的子树的方案数有(j!)种,然后剩下的(n-i-j)个节点随便放,第一个节点可以放置的方案是(i)种,第二个是(i+1)种,那么剩下节点随便放的贡献就是(frac{(n-j)!}{(i-1)!}),总贡献就是:$$sum_{i=1}{n}sum_{j=1}{n-i}i!2C_{n-i}^jj!j(n-j)frac{(n-j)!}{(i-1)!}$$
因为不一定存在逆元,可以先递推杨辉三角,然后把最后那部分用组合数乘阶乘的形式表示出来.
当然这题也有(DP)的解法,有兴趣可以自己看看别的题解
#include<bits/stdc++.h>
using namespace std;
const int N = 2000+5;
int n, mod, fac[N], c[N][N], ans = 0;
int main(){
cin >> n >> mod; c[0][0] = fac[0] = fac[1] = 1;
for(int i = 1; i <= n; i++){
c[i][0] = 1;
for(int j = 1; j <= n; j++) c[i][j] = (c[i-1][j]+c[i-1][j-1])%mod;
}
for(int i = 1; i <= n; i++) fac[i] = 1ll*fac[i-1]*i%mod;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n-i; j++)
(ans += 1ll*fac[i]*2%mod*c[n-i][j]%mod*fac[j]%mod*j%mod*(n-j)%mod*c[n-j-1][n-i-j]%mod*fac[n-i-j]%mod) %= mod;
cout << ans << endl;
return 0;
}