题目描述
地平线(x轴)上有n个矩(lou)形(fang),用三个整数h[i],l[i],r[i]来表示第i个矩形:矩形左下角为(l[i],0),右上角为(r[i],h[i])。地平线高度为0。在轮廓线长度最小的前提下,从左到右输出轮廓线。
下图为样例2。
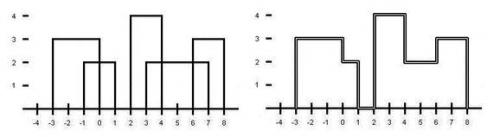
输入输出格式
输入格式:
第一行一个整数n,表示矩形个数
以下n行,每行3个整数h[i],l[i],r[i]表示第i个矩形。
输出格式:
第一行一个整数m,表示节点个数
以下m行,每行一个坐标表示轮廓线上的节点。从左到右遍历轮廓线并顺序输出节点。第一个和最后一个节点的y坐标必然为0。
输入输出样例
说明
【数据范围】
对于30%的数据,n<=100
对于另外30%的数据,n<=100000,1<=h[i],l[i],r[i]<=1000
对于100%的数据,1<=n<=100000,1<=h[i]<=10^9,-10^9<=l[i]<r[i]<=10^9
先留一点思考的时间
题解:
题意就是给出一张图形的坐标 ,求出这张图中的拐点个数和坐标.
对于60%的数据,可以直接模拟加离散化. 用数组存下每一个X轴上的点的最高值,但是为什么要用离散化呢?
当遇到这样的情况时,代码就会出问题:
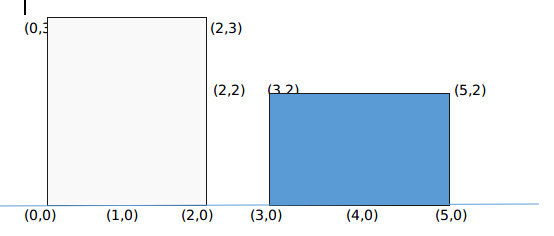
h[2]=3, h[3]=2,那么在循环扫过来时就不会处理(2,0)和(3,0),但这两个点是存在的,所以要用离散化,将一格坐标变为两格坐标:
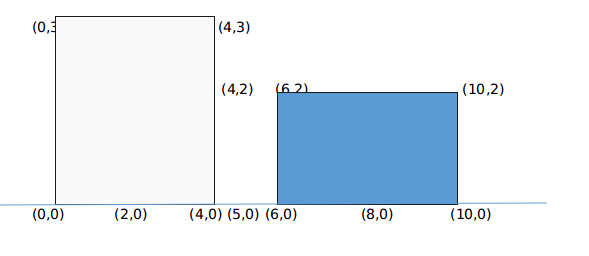
这样的话循环只会多一点常数,但是答案能保证正确.
对于100%的数据:
可以用离散化加线段树或扫描线.
离散化加线段树的方法与暴力相类似,用线段树加速了区间最值的修改与查询.
扫描线
将矩形的左右两边看作是一条线段,分别是一个矩形的入边和出边,然后通过排序确定遍历扫描线的顺序.这样就可以在O(nlogn)的时间复杂度内完成.
那么扫描线应该怎么排序呢?
我们用扫描线就是为了确定一个矩形的覆盖情况,然后找到图中的拐点.那么首先就应该是要按照X轴上的坐标进行排序.并且应该先扫入边,再扫出边,这样可以保证不会有什么鬼的奇怪的数据有左右边相同的矩形使得结果出问题. 在判断完前两种情况后,现在正在排序的两条线就同属于一种边(同为入边或出边),那么若是入边,则越高越容易挡住另一个矩形,就要放在前面才会使得更新一次答案时没有矩形被挡住.若是出边,则越低越容易被挡住,则要放在后面,这样就可以使得高的出边在后面被扫到,就可以保证在删除最后一条出边时更新答案没有矩形被挡住.
1 bool cmpl(line a,line b){ 2 if(a.x!=b.x) return a.x<b.x; 3 if(a.f!=b.f) return a.f<b.f; 4 if(a.f==1) return a.h>b.h; 5 if(a.f==2) return a.h<b.h; 6 }
然后在后面扫描的时候就直接用for循环遍历每一条扫描线.那么扫到一条扫描线就有两种情况:
- 属于入边,如果比当前最高值还要高,则出现了拐点,更新答案.
- 属于出边,如果高度为当前最大高度且该高度出边只有一条,则出现了拐点,更新答案.
这里记录当前已经加入扫描的矩形时用了一个STL容器:multiset.这个东西与set不同的地方体现在它可以存入相同的元素,且默认单调递增,那么对于这个题目的实现就提供了一个很好的帮助.
C++ STL MultiSet类成员函数列表如下:
clear() 清除所有元素
count() 返回指向某个值元素的个数
end() 返回指向最后一个元素的迭代器
equal_range() 返回集合中与给定值相等的上下限的两个迭代器
erase() 删除集合中的元素
find() 返回一个指向被查找到元素的迭代器
insert() 在集合中插入元素
key_comp() 返回一个用于元素间值比较的函数
lower_bound() 返回指向大于(或等于)某值的第一个元素的迭代器
rbegin() 返回指向多元集合中最后一个元素的反向迭代器
rend() 返回指向多元集合中第一个元素的反向迭代器
size() 多元集合中元素的数目
upper_bound() 返回一个大于某个值元素的迭代器
value_comp() 返回一个用于比较元素间的值的函数
然后把答案存到数组里,根据题目要求输出.
下面是代码:
#include<bits/stdc++.h> using namespace std; const int N=100005; int n; int cnt=0; int cnta=0; struct line{ int x,h,f; }l[N*2]; struct answer{ int x,y; }ans[N*4]; int gi(){ int ans=0,f=1;char i=getchar(); while(i<'0'||i>'9'){if(i=='-')f=-1;i=getchar();} while(i>='0'&&i<='9'){ans=ans*10+i-'0';i=getchar();} return ans*f; } bool cmpl(line a,line b){ if(a.x!=b.x) return a.x<b.x; if(a.f!=b.f) return a.f<b.f; if(a.f==1) return a.h>b.h; if(a.f==2) return a.h<b.h; } int main(){ //freopen("Fort.in","r",stdin); //freopen("Fort.out","w",stdout); n=gi(); for(int i=1,x,y,z;i<=n;i++){ x=gi(); y=gi(); z=gi(); l[++cnt].x=y; l[cnt].h=x; l[cnt].f=1; l[++cnt].x=z; l[cnt].h=x; l[cnt].f=2; } sort(l+1,l+cnt+1,cmpl); multiset <int> s; s.insert(0); for(int i=1;i<=cnt;i++){ int maxh=*s.rbegin(); if(l[i].f==1){ if(l[i].h>maxh){ ans[++cnta].x=l[i].x; ans[cnta].y=maxh; ans[++cnta].x=l[i].x; ans[cnta].y=l[i].h; } s.insert(l[i].h); } if(l[i].f==2){ if(l[i].h==maxh&&s.count(maxh)==1){ s.erase(maxh); ans[++cnta].x=l[i].x; ans[cnta].y=l[i].h; ans[++cnta].x=l[i].x; ans[cnta].y=*s.rbegin(); } else s.erase(s.find(l[i].h)); } } cout<<cnta<<endl; for(int i=1;i<=cnta;i++) printf("%d %d ",ans[i].x,ans[i].y); return 0; }