洛谷题目链接:滑动窗口
题目描述
现在有一堆数字共N个数字(N<=10^6),以及一个大小为k的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
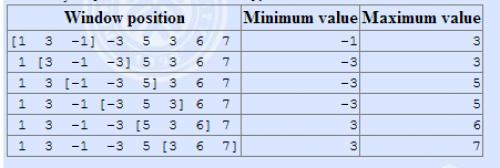
输入输出格式
输入格式:
输入一共有两行,第一行为n,k。
第二行为n个数(小于INT_MAX).
输出格式:
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
输入输出样例
输入样例#1:
8 3
1 3 -1 -3 5 3 6 7
输出样例#1:
-1 -3 -3 -3 3 3
3 3 5 5 6 7
说明
50%的数据,n<=10^5
100%的数据,n<=10^6
解释一下题意:给出一个长度为N的序列,以及一个滑动窗口的长度k.要求出每一次移动后当前位置滑动窗口上的最大值和最小值.
看这个数据范围,用数据结构什么的是很难过的,很可能被卡常或者是爆空间什么的.所以这里提供了一种神奇的做法:
单调队列
我们来模拟一下样例的序列(求滑动窗口最大值):1 3 -1 -3 5 3 6 7. * 首先是1入队. * 然后3入队判断,3比1大,而1又在3前面,所以1比3会先出队,意味着1在有生之年是当不成最大值了,所以1可以出队了.此时最大值是队首3. * 接着-1入队判断.-1比3小,说明如果3出队了-1还是有可能成为最大值的.所以-1直接入队.最大值仍是队首3. * -3入队判断,比-1小,仍有可能成为最大值,先入队.此时最大值依旧是队首3. * 5入队判断,比队尾大,说明之前入队的-3,-1,3都不可能成为最大值了.于是把它们都出队.把5入队,此时最大值是队首5. * 3入队同理. * 6入队,弹出3,5.最大值是6. * 7入队,弹出6,最大值是7.
那么我们大概就得出了优先队列的维护方法: * 每个元素入队前判断它之前的元素是否可能成为最值.将不可能成为最值的元素都弹出队. * 将该元素入队. * 统计当前状态下队列的元素个数,从队首开始弹出一定数量元素保证队列中元素个数在滑动窗口大小内. * 此时队首的值就是维护的最值.
具体在操作过程中可以用两个数组模拟队列,一个记录元素的值来判断是否可能成为最值.另一个记录元素下标来判断当前队列元素个数.
下面看一下代码注释:
#include<bits/stdc++.h>
using namespace std;
const int N=1000000+5;
const int inf=2147483647;
int n, k, w[N];
int q1[N], q2[N];//q1统计元素的值,q2统计下标.
int gi(){//读入优化
int ans = 0 , f = 1; char i = getchar();
while(i<'0'||i>'9'){if(i=='-')f=-1;i=getchar();}
while(i>='0'&&i<='9'){ans=ans*10+i-'0';i=getchar();}
return ans * f;
}
int main(){
int h, t; n = gi(); k = gi();
for(int i=1;i<=n;i++) w[i] = gi();
h = 1; t = 0;
for(int i=1;i<=n;i++){
while(h <= t && q1[t] >= w[i]) t--;//如果队列中有元素且之前的元素都不可能成为要统计的最值,那么直接将该元素弹出.
q1[++t] = w[i]; q2[t] = i;//入队.
if(i-k >= q2[h]) h++;//如果当前队列的大小超过了滑动窗口限定的大小,则从队首开始弹出元素.
if(i >= k) printf("%d ",q1[h]);//此时队首统计的就是当前滑动窗口的最值.
}
printf("
"); h = 1; t = 0;//
for(int i=1;i<=n;i++){
while(h <= t && q1[t] <= w[i]) t--;
q1[++t] = w[i]; q2[t] = i;
if(i-k >= q2[h]) h++;
if(i >= k) printf("%d ",q1[h]);
}
printf("
");
return 0;
}