Codeforces Round #459 (Div. 2) D. MADMAX

D. MADMAX

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

As we all know, Max is the best video game player among her friends. Her friends were so jealous of hers, that they created an actual game just to prove that she's not the best at games. The game is played on a directed acyclic graph (a DAG) with n vertices and m edges. There's a character written on each edge, a lowercase English letter.

Max and Lucas are playing the game. Max goes first, then Lucas, then Max again and so on. Each player has a marble, initially located at some vertex. Each player in his/her turn should move his/her marble along some edge (a player can move the marble from vertex v to vertex u if there's an outgoing edge from v to u). If the player moves his/her marble from vertex v to vertex u, the "character" of that round is the character written on the edge from v to u. There's one additional rule; the ASCII code of character of round i should be greater than or equal to the ASCII code of character of round i - 1 (for i > 1). The rounds are numbered for both players together, i. e. Max goes in odd numbers, Lucas goes in even numbers. The player that can't make a move loses the game. The marbles may be at the same vertex at the same time.

Since the game could take a while and Lucas and Max have to focus on finding Dart, they don't have time to play. So they asked you, if they both play optimally, who wins the game?

You have to determine the winner of the game for all initial positions of the marbles.

Input

The first line of input contains two integers n and m (2 ≤ n ≤ 100, ).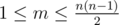

The next m lines contain the edges. Each line contains two integers v, u and a lowercase English letter c, meaning there's an edge from vto u written c on it (1 ≤ v, u ≤ n, v ≠ u). There's at most one edge between any pair of vertices. It is guaranteed that the graph is acyclic.

Output

Print n lines, a string of length n in each one. The j-th character in i-th line should be 'A' if Max will win the game in case her marble is initially at vertex i and Lucas's marble is initially at vertex j, and 'B' otherwise.

Examples

input

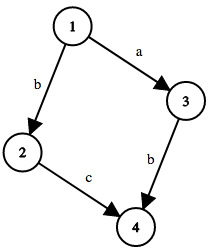
4 4
1 2 b
1 3 a
2 4 c
3 4 b

output

BAAA
ABAA
BBBA
BBBB

input

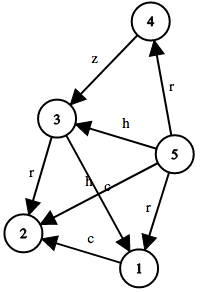
5 8
5 3 h
1 2 c
3 1 c
3 2 r
5 1 r
4 3 z
5 4 r
5 2 h

output

BABBB
BBBBB
AABBB
AAABA
AAAAB

Note

Here's the graph in the first sample test case:

Here's the graph in the second sample test case:

 思路：枚举两人位置，当前边限制，当前轮次的玩家，n*n*26*2的状态数，记忆化搜索/dp 一下就行了。

#include <iostream>
#include <fstream>
#include <sstream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <iomanip>
#include <cctype>
#include <cassert>
#include <bitset>
#include <ctime>

using namespace std;

#define pau system("pause")
#define ll long long
#define pii pair<int, int>
#define pb push_back
#define mp make_pair
#define clr(a, x) memset(a, x, sizeof(a))

const double pi = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const double EPS = 1e-9;

int n, m;
int dp[105][105][26][2];
struct edge {
    int v;
    char c;
    edge () {}
    edge (int v, char c) : v(v), c(c) {}
};
vector<edge> E[105];
int dfs(int i, int j, int k, int l) {
    if (~dp[i][j][k][l]) {
        return dp[i][j][k][l];
    }
    int res, tres;
    if (l) {
        res = 1, tres = 1;
        for (int rep = 0; rep < E[j].size(); ++rep) {
            int v = E[j][rep].v;
            char c = E[j][rep].c;
            if (c >= 'a' + k) {
                tres = dfs(i, v, c - 'a', !l);
                res = min(res, tres);
            }
        }
    } else {
        res = 0, tres = 0;
        for (int rep = 0; rep < E[i].size(); ++rep) {
            int v = E[i][rep].v;
            char c = E[i][rep].c;
            if (c >= 'a' + k) {
                tres = dfs(v, j, c - 'a', !l);
                res = max(res, tres);
            }
        }
    }
    return dp[i][j][k][l] = res;
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; ++i) {
        int u, v;
        char c;
        scanf("%d%d %c", &u, &v, &c);
        E[u].pb(edge(v, c));
    }
    clr(dp, -1);
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            putchar(dfs(i, j, 0, 0) ? 'A' : 'B');
        }
        puts("");
    }
    return 0;
}