You are given a multiset S consisting of positive integers (initially empty). There are two kind of queries:
- Add a positive integer to S, the newly added integer is not less than any number in it.
- Find a subset s of the set S such that the value
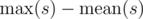is maximum possible. Here max(s) means maximum value of elements in s, 
— the average value of numbers in s. Output this maximum possible value of .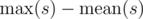
The first line contains a single integer Q (1 ≤ Q ≤ 5·105) — the number of queries.
Each of the next Q lines contains a description of query. For queries of type 1 two integers 1 and x are given, where x (1 ≤ x ≤ 109) is a number that you should add to S. It's guaranteed that x is not less than any number in S. For queries of type 2, a single integer 2 is given.
It's guaranteed that the first query has type 1, i. e. S is not empty when a query of type 2 comes.
Output the answer for each query of the second type in the order these queries are given in input. Each number should be printed in separate line.
Your answer is considered correct, if each of your answers has absolute or relative error not greater than 10 - 6.
Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if 
.
6
1 3
2
1 4
2
1 8
2
0.0000000000
0.5000000000
3.0000000000
4
1 1
1 4
1 5
2
2.0000000000
思路一：要想使max - mean最小，max肯定要选取最大值，因为任意不取当前最大值a[p]的取法都可以用a[p]取代当前取到的最大值，从而结果更优。在此情况下要想使mean最小，
一定是把前k小的一坨值全取了。可以证明出查询结果是关于k的单峰函数。因此直接三分就好了。
#include <iostream> #include <fstream> #include <sstream> #include <cstdlib> #include <cstdio> #include <cmath> #include <string> #include <cstring> #include <algorithm> #include <queue> #include <stack> #include <vector> #include <set> #include <map> #include <list> #include <iomanip> #include <cctype> #include <cassert> #include <bitset> #include <ctime> using namespace std; #define pau system("pause") #define ll long long #define pii pair<int, int> #define pb push_back #define mp make_pair #define clr(a, x) memset(a, x, sizeof(a)) const double pi = acos(-1.0); const int INF = 0x3f3f3f3f; const int MOD = 1e9 + 7; const double EPS = 1e-9; int q, op, x, num; int a[500015]; double sum[500015]; double cal(int p, int y) { return (sum[p] + y) / (p + 1); } int main() { scanf("%d", &q); while (q--) { scanf("%d", &op); if (1 == op) { scanf("%d", &a[++num]); sum[num] = sum[num - 1] + a[num]; } else { int y = a[num]; int l = 1, r = num - 1; while (l <= r - 3) { int lm = (l * 2 + r) / 3; int rm = (l + r * 2) / 3; if (cal(lm, y) > cal(rm, y)) { l = lm; } else { r = rm; } } double res = 0; for (int i = l; i <= r; ++i) { if (y - cal(i, y) > res) res = y - cal(i, y); } printf("%.12f ", res); } } return 0; }
思路二：赛后想了想，这个可以二分的。因为我们肯定取前k小，若i被取，一定有(sum[i - 1] + a[p]) / i <= a[i]，反之则不被取，因为取它的话mean值会升高，故二分
取到最后一个元素的位置就行了。
#include <iostream> #include <fstream> #include <sstream> #include <cstdlib> #include <cstdio> #include <cmath> #include <string> #include <cstring> #include <algorithm> #include <queue> #include <stack> #include <vector> #include <set> #include <map> #include <list> #include <iomanip> #include <cctype> #include <cassert> #include <bitset> #include <ctime> using namespace std; #define pau system("pause") #define ll long long #define pii pair<int, int> #define pb push_back #define mp make_pair #define clr(a, x) memset(a, x, sizeof(a)) const double pi = acos(-1.0); const int INF = 0x3f3f3f3f; const int MOD = 1e9 + 7; const double EPS = 1e-9; int q, num, a[500015], op, x; double sum[500015]; bool ok(int p, int y) { return a[p] < (sum[p - 1] + y) / p; } int main() { scanf("%d", &q); while (q--) { scanf("%d", &op); if (1 == op) { scanf("%d", &x); a[++num] = x; sum[num] = sum[num - 1] + x; } else { int y = a[num]; int s = 1, e = num - 1, mi, ans = 0; while (s <= e) { mi = s + e >> 1; if (ok(mi, y)) s = (ans = mi) + 1; else e = mi - 1; } double res = 0; if (ans) res = y - (sum[ans] + y) / (ans + 1); printf("%.12f ", res); } } return 0; }
思路三：因为被取元素要小于前缀和+最大值的平均值，每次查询的最大值非严格递增，因此平均值非严格递增，故取到的终止位置非严格递增。因此我们不需要二分查找，每次从上次查询取到的位置继续往后判断就行了。复杂度O(q)。
#include <iostream> #include <fstream> #include <sstream> #include <cstdlib> #include <cstdio> #include <cmath> #include <string> #include <cstring> #include <algorithm> #include <queue> #include <stack> #include <vector> #include <set> #include <map> #include <list> #include <iomanip> #include <cctype> #include <cassert> #include <bitset> #include <ctime> using namespace std; #define pau system("pause") #define ll long long #define pii pair<int, int> #define pb push_back #define mp make_pair #define clr(a, x) memset(a, x, sizeof(a)) const double pi = acos(-1.0); const int INF = 0x3f3f3f3f; const int MOD = 1e9 + 7; const double EPS = 1e-9; int q, num, a[500015], op, x, pre; double sum[500015]; bool ok(int p, int y) { return a[p] < (sum[p - 1] + y) / p; } int main() { scanf("%d", &q); while (q--) { scanf("%d", &op); if (1 == op) { scanf("%d", &x); a[++num] = x; sum[num] = sum[num - 1] + x; } else { int y = a[num]; while (pre < num && ok(pre + 1, y)) ++pre; double res = 0; if (pre) res = y - (sum[pre] + y) / (pre + 1); printf("%.12f ", res); } } return 0; }