2015 USP-ICMC gym 100733 J. Summer Wars

J. Summer Wars

time limit per test

2.0 s

memory limit per test

64 MB

input

standard input

output

standard output

The mafia is finally resting after a year of hard work and not so much money. Mafianca, the little mascot of the gang wanted to go to the beach.

Little did they know that the rival gang had prepared a trap to the little girl and her rubber duck. They know that Mafianca, despite loving the beach, hates water. So they set up some water sprayers to ruin her day. The beach can be seen as a plane. The sprayers are located at different (x, y) points along the shore. Each sprayer is so strong that it creates an infinite line of water, reaching every point with x-coordinate equal to the sprayer.

Mafianca's bodyguards figured this plan out. They didn't have the time to destroy the sprayers, so they decided to do something else. Lying around on the beach was a piece of modern art: a bunch of walls, represented by horizontal line segments, painted by some futuristic anonymous artist. Those walls can be moved, but they can only be moved together and horizontally.

The bodyguards decided that they would try to move this piece of art in order to block the most sprayers they can. A sprayer is blocked if there's at least one wall in both of its sides.

How many sprayers can they block?

Input

Input begins with the number of sprayers, n (1 ≤ n ≤ 1000) and the number of walls in the modern art, m (1 ≤ m ≤ 1000).

Follows n lines, each with two intergers, y and x (0 ≤ y, x ≤ 106), indicating that there's a sprayer at position x, y.

Then follows m lines, each with three integers: y, xbegin and xend (0 ≤ y ≤ 106) and (0 ≤ xbegin < xend ≤ 106) denoting a wall in the modern art has y-coordinate y, begins at xbegin and ends at xend. No wall will have a y-coordinate shared with a sprayer and the walls with same ywill not intersect.

Output

Print the number of sprayers that can be blocked.

Examples

input

Copy

1 1
2 2
3 1 3

output

Copy

0

input

Copy

2 5
2 3
2 6
1 0 2
4 0 4
0 2 3
1 4 5
3 5 7

output

Copy

2

input

Copy

4 5
2 3
2 8
2 20
5 1
1 0 2
4 0 4
0 2 3
1 4 5
3 5 7

output

Copy

2

input

Copy

3 4
2 0
2 4
4 7
1 0 2
3 1 3
5 0 2
5 3 4

output

Copy

2

Note

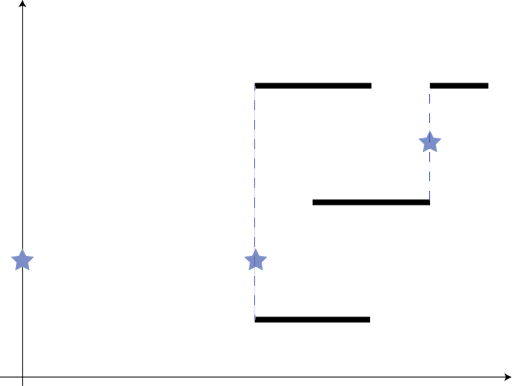
In the test case #4, the beach looks like this:

A solution would be

思路：枚举所有的移动长度的话，每个星星对整体的贡献都是多段区间。因为只有最终一次查询，我们建立一个差分数组。将线段按x排序后，类似差分方法，左端点在set里入y，右端点出y，对于每个星星，只需判断集合中的y和星星的y之间的关系。然后用星星的x计算出相对位移O(m)更新差分数组。最后求差分数组前缀和最大值。复杂度O(nmlog(m) + D)。

#include <iostream>
#include <fstream>
#include <sstream>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector>
#include <set>
#include <map>
#include <list>
#include <iomanip>
#include <cctype>
#include <cassert>
#include <bitset>
#include <ctime>

using namespace std;

#define pau system("pause")
#define ll long long
#define pii pair<int, int>
#define pb push_back
#define mp make_pair
#define clr(a, x) memset(a, x, sizeof(a))

const double pi = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int MOD = 1e9 + 7;
const double EPS = 1e-9;
const int D = 1e6;

/*
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>

using namespace __gnu_pbds;
tree<pli, null_type, greater<pli>, rb_tree_tag, tree_order_statistics_node_update> T;
*/

int n, m;
struct point {
    int x, y;
    point () {}
    point (int x, int y) : x(x), y(y) {}
    bool operator < (const point &p) const {
        return x < p.x;
    }
} P[1015];
int cnt[2000015], con[2015], tcnt[2015];
map<int, int> mmp;
set<int> ss;
pii p[2015];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i) {
        scanf("%d%d", &P[i].y, &P[i].x);
    }
    for (int i = 1; i <= m; ++i) {
        int y, xs, xe;
        scanf("%d%d%d", &y, &xs, &xe);
        p[i * 2 - 1] = pii(xs, y);
        p[i * 2] = pii(xe + 1, y - 2 * D);
        mmp[xs]; mmp[xe + 1];
    }
    int cnt_index = 0;
    for (map<int, int>::iterator it = mmp.begin(); it != mmp.end(); ++it) {
        it -> second = ++cnt_index;
        con[cnt_index] = it -> first;
    }
    sort(p + 1, p + 2 * m + 1);
    for (int i = 1; i <= n; ++i) {
        ss.clear();
        clr(tcnt, 0);
        for (int j = 1; j <= 2 * m; ) {
            int k = j;
            while (k <= 2 * m && p[k].first == p[j].first) {
                if (p[k].second < 0) ss.erase(p[k].second + 2 * D);
                else ss.insert(p[k].second);
                ++k;
            }
            if (ss.lower_bound(P[i].y) != ss.begin() && ss.lower_bound(P[i].y) != ss.end()) {
                tcnt[mmp[p[j].first]] = 1;
            } else {
                tcnt[mmp[p[j].first]] = 0;
            }
            j = k;
        }
        for (int j = 1; j < cnt_index; ++j) {
            if (tcnt[j]) {
                ++cnt[D + con[j] - P[i].x];
                --cnt[D + con[j + 1] - P[i].x];
            }
        }
    }
    int ans = cnt[0];
    for (int i = 1; i <= 2 * D; ++i) {
        cnt[i] += cnt[i - 1];
        ans = max(ans, cnt[i]);
    }
    printf("%d
", ans);
    return 0;
}