平衡树之splay讲解

　　首先来说是splay是二叉搜索树，它可以说是线段树和SBT的综合，更可以解决一些二者解决不了的问题，splay几乎所有的操作都是由splay这一操作完成的，在介绍这一操作前我们先介绍几个概念和定义

　　二叉搜索树，即BST(binary search tree)，这样的树有一个关键字，满足对于每个节点来说，以该节点左儿子为根节点的子树中的所有节点的关键字小于该节点的关键字，以该节点右儿子为根节点的子树中的所有节点的关键字大于该节点的关键字。

　　splay主要可以用来解决区间的维护问题

　　假设我们需要维护一个数列，支持

　　1.在数列第i位后插入一个长为l的数列

　　2.在数列第i为后删除一个长为l的数列　

　　3.将数列的l r区间翻转（1 2 3  2 3 翻转后为 3 2 3 2 1）

　　4.将数列的l r区间同时加上一个值

　　5.将数列的l r区间同时改为一个值

　　6.求数列的l r区间的和（最大值）

　　其实线段树上的大部分操作这里都支持，比如区间最大子区间和

　　首先对于当前的树，它的中序遍历就是当前的区间，每个点的关键字（二叉搜索树的那个）是内个点表示区间元素的标号，比如一个点的关键字是3，那么这个点代表区间中第3个元素，每个点除了关键字外还记录了一个tree[i]代表这个点对应区间内的元素是什么。

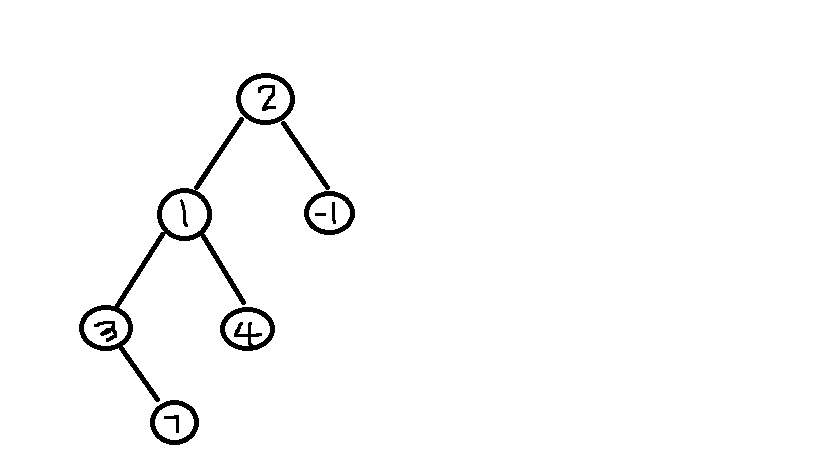
　　上图（节点内的数代表tree值）的树表示数列 3 7 1 4 2 -1

　　对于每个节点的记录内容为

　　son[x,0..1]左右儿子

　　father[x]父亲节点

　　还有我们定义root为当前树的根节点，sroot为超级节点（-1），sroot只连接着root（其实就是定义了root的father为-1）

　　那么我们首先建树的时候，具体过程为

function build(l,r:longint):longint;
var
    mid                            :longint;
begin
    mid:=(l+r) div 2;
    tree[mid]:=a[mid];//a为区间的值
    if l<=mid-1 then 
    begin
          son[mid,0]:=build(l,mid-1);
          father[son[mid,0]]:=mid;
    end;
    if mid+1<=r then 
    begin
          son[mid,1]:=build(mid+1,r);
          father[son[mid,1]]:=mid;
    end;
    update(mid);//可暂时忽略
    exit(mid);
end;

　　那么我们现在有了一颗树，我们还需要改变这棵树的形态，就是splay（x,y）代表将编号为x的点旋转到y的儿子处，那么我们就需要介绍一个旋转操作了，在介绍旋转操作之前还应该引入一个find操作，假设我们需要找区间内第i个元素，树中代表这个点的编号是多少（每个点都有一个编号，编号随意定，满足互不相同就行了，类似于线段树，SBT中的点的编号，没有实际意义）我们规定一个点的size值为以该点为根节点的子树的节点数，那么find（l）表示数列中第l个元素在树中的编号。

function find(x:longint):longint;
var 
    t                        :longint;
begin
    t:=root;    
    while true do
    begin
        push_down(t);//可暂时忽略
        if size[son[t,0]]+1=x then exit(t);
        if size[son[t,0]]+1>x then t:=son[t,0]
        else
            begin
                dec(x,size[son[t,0]]+1);
                t:=son[t,1];
            end;
    end;
end;

　　那么我们介绍旋转过程rotate(x,y)代表将编号为x的节点旋转到他的父亲节点，就是如果x是左儿子就右旋father[x]，右儿子就左旋father[x]，y代表x是他父亲的左节点（0）还是右节点（1）。

procedure rotate(x,y:longint);
var 
    f                        :longint;
begin
    push_down(x);
    f:=father[x];
    father[son[x,y xor 1]]:=f;
    son[f,y]:=son[x,y xor 1];
    if f=root then root:=x
    else
        if f=son[father[f],0] then 
            son[father[f],0]:=x else 
            son[father[f],1]:=x;
    father[x]:=father[f];
    father[f]:=x;
    son[x,y xor 1]:=f;
    update(f);
    update(x);
end;

　　那么对于splay过程我们就可以理解了

procedure splay(x,y:longint);
var 
    u, v                    :longint;
begin
    while father[x]<>y do
        if father[father[x]]=y then 
            rotate(x,ord(x=son[father[x],1])) else
        begin
            if son[father[x],0]=x then u:=1 else u:=-1;
            if son[father[father[x]],0]=father[x] then v:=1 else v:=-1;
            if u*v=1 then
            begin
                rotate(father[x],ord(x=son[father[x],1]));
                rotate(x,ord(x=son[father[x],1]));
            end else
            begin
                rotate(x,ord(x=son[father[x],1]));
                rotate(x,ord(x=son[father[x],1]));
            end;
        end;
    update(x);
end;

　　其中u=1代表x是父亲的左节点，u=-1代表是右节点，v=1代表x父亲是x爷爷的左节点，v=-1代表右节点

　　那么v*u=1的情况就是x和父亲，爷爷，祖孙三代是一条链（直观的说）这种情况先旋父亲，再旋x，否则旋两次x,其实结果是一样的，但是前人证明这样操作会使splay树更平衡些。

　　那么剩下的操作就是基于这几个操作的扩展了，比如添加区间，在l后加入长s的区间

for i:=n+1 to n+s do read(a[i]);
p:=build(n+1,n+s);//把这一区间建成一棵树我们只需要插入p节点就行了
q:=find(l); splay(q,sroot);
q:=find(l+1); splay(q,root);
son[son[root,1],0]:=p;
father[p]:=son[root,1];
update(son[root,1]);
update(root);

　　其中两个find和splay操作是精华，我们先找到第l个元素，旋转到根，再找到第l+1个元素，旋转到根的右儿子，那么第l+1个节点是没有左儿子的（因为当前以l为根，l+1元素左儿子代表比l大的，比l+1小的，显然没有），那么我们不是要在L后面插入区间么，就直接将p点当成l+1点的左儿子就行了。

　　那么我们会发现，假如我要在区间的开头插入区间怎么办find（0）是没有值的，那么我们就插入左右标兵，在最开始建树的时候inc（n），root:=build(0,n)；

　　其实这样多插入了两个数，那么我们要find(l)时需要find(l+1)，以后每次用find的时候+1就好了

　　那么对于删除操作假设删除l r区间

p:=find(l); splay(p,sroot);
p:=find(r+2); splay(p,root);
son[son[root,1],0]:=-1;
update(son[root,1]);
update(root);

　　我们将区间中第l-1个元素旋转到根节点，r+1个元素旋转到根节点的右儿子，那么以son[son[root,1],0]为根节点的子树代表的就是区间l r，直接删除就好，那么对于区间最大值操作，类似于线段树就行了，因为旋转后树的结构已经改变了，那么我们需要维护节点存储的信息，就是update操作

procedure update(x:longint);
begin
    sum[x]:=sum[son[x,0]]+tree[x]+sum[son[x,1]];
    size[x]:=size[son[x,0]]+1+size[son[x,1]];
    max[x]:=get_max(tree[x],get_max(max[son[x,0]],max[son[x,1]]));
end;

　　对于区间赋值，修改这样的，打标签就好了，那么对于区间翻转操作我们也可以打标签，flag[x]为true代表以x为根节点的区间需要翻转，那么我们旋转一个区间的时候，假设根节点为x。

proceudre reverse(x:longint);
begin
     swap(son[x,1],son[x,0]);
     flag[son[x,1]]:=not flag[son[x,1]];
     flag[son[x,0]]:=not flag[son[x,0]];
end;    

　　可以自己举个例子，发现满足这个性质

　　push_down操作则为下放标签

procedure push_down(x:longint);
var 
    l,r                        :longint;
begin
    l:=son[x,0];r:=son[x,1];
    if flag[x] then
        begin
            if l<>-1 then renew(l,0);
            if r<>-1 then renew(r,0);
            flag[x]:=false;
        end;
    if val[x]<>0 then
        begin
            if l<>-1 then renew(l,val[x]);
            if r<>-1 then renew(r,val[x]);
            val[x]:=0;
        end;
end;