重庆2019acm市赛

A. 狂小P猜密码

思路

从题意可知，十个数中有 (1-4) 个 (1) 时是存在方案的，其他情况答案都是 (0)。

已知一多重集，共 (n) 个数，其中 (n_1) 个 (a_1)，(n_2) 个 (a_2)，...，(n_k) 个 (a_k)。其全排列数为：

[frac{n!}{n_1!cdot n_2!cdot...cdot n_k!} ]

可知，当有 (1) 个 (1) 时，答案为 (1)。

当有 (2) 个 (1) 时，可能是一个数出现 (3) 次，另一个数出现 (1) 次；也可能是两个数都出现两次。答案为：

[2 imesfrac{4!}{3!}+frac{4!}{2!+2!}=8+6=14 ]

当有 (3) 个 (1) 时，有一个数出现两次，另外两个数出现 (1) 次。答案为：

[3 imesfrac{4!}{2!}=36 ]

当有 (4) 个 (1) 时，四个数各出现一次，答案为 (4!=24) 。

代码

#include <bits/stdc++.h>
using namespace std;

int main(){
	int num=0;
	for(int i=1,x;i<=10;i++){
		scanf("%d",&x);
		num+=x;
	}
	if(num==1) printf("1");
	else if(num==2) printf("14");
	else if(num==3) printf("36");
	else if(num==4) printf("24");
	else printf("0");
	return 0;
}

B. cyy的珍珠奶茶

思路

设大圆半径为 (R)，小圆半径为 (r)，有 (n) 个小圆。

如果 (n=1)，(r=R)

如果 (n=2)，(r=frac{R}{2})

如果 (ngeq 3)，看图

[a=frac{pi}{n}\r=frac{sin(a)}{1+sin(a)}R ]

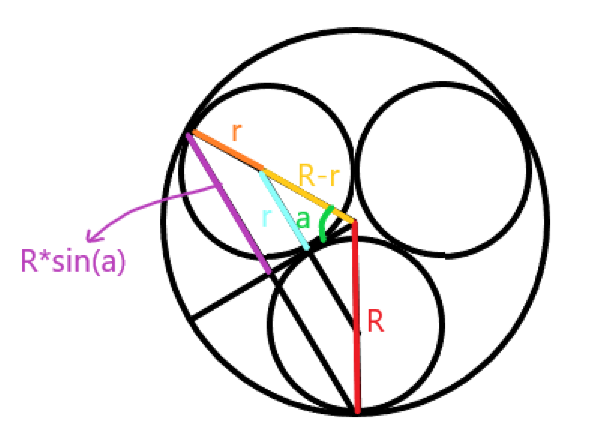
代码

#include <bits/stdc++.h>
using namespace std;
int T;
double r,n;

int main(){
	scanf("%d",&T);
	while(T--){
		scanf("%lf%lf",&r,&n);
		if(n==1) {printf("%lf
",r);continue;}
		if(n==2) {printf("%lf
",r/2);continue;}
		double a=3.1415926535/n;
		double ans=sin(a)/(1+sin(a))*r;
		printf("%lf
",ans);
	}
	return 0;
}

F. JiangYu的机器人

签到题

代码

#include <bits/stdc++.h>
using namespace std;
int T,n,x,y,k;

int main(){
	scanf("%d",&T);
	while(T--){
		scanf("%d%d%d%d",&n,&k,&x,&y);
		if((y-1)%k==0||(n-y)%k==0||(y-x)%k==0)
			printf("YES
");
		else printf("NO
");
	}
	return 0;
}

G. cyy买奶茶

思路

01分数规划+树形Dp

可以发现题目给了一颗 (n+1) 个节点的树，编号从 (0) 到 (1)。

要求从 (0) 走出，要最后要回到 (0)。可知，走过的每条边累计走两次。

设第 (i) 个节点点权 (a_i)，连接其父节点的边的边权为 (b_i)。

那么本题要求的就是 (frac{sum_{i=1}^{n}x_icdot a_i}{sum_{i=1}^{n}x_icdot 2cdot b_i} (x_i=0 或 1)) 的最大值

这就是一个典型的01分数规划的问题，解法是用二分，具体可以百度

然而这个题中每个节点之间是有依赖关系的。

那么二分的验证就是一个树形Dp，每个节点都要取到最优的价值。

代码

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e5+10;
int n,head[MAXN],to[MAXN*2],nxt[MAXN*2],val[MAXN*2],tot,c[MAXN];
 
void add(int u,int v,int w){
	to[++tot]=v;val[tot]=w;nxt[tot]=head[u];head[u]=tot;
}
 
double sum[MAXN];
void dfs(int u,int fa,int len,double L){
	for(int i=head[u];i;i=nxt[i])
		if(to[i]!=fa)
			dfs(to[i],u,val[i]*2,L);
	sum[u]=1.0*c[u]-L*len;
	for(int i=head[u];i;i=nxt[i])
		if(to[i]!=fa&&sum[to[i]]>0)
			sum[u]+=sum[to[i]];
}
 
 
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&c[i]);
	for(int i=1,u,v,w;i<=n;i++){
		scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);add(v,u,w);
	}
	double l=0,r=1e9;
	while(r-l>1e-8){
		double mid=(l+r)/2;
		dfs(0,0,0,mid);
		if(sum[0]>0) l=mid;
		else r=mid;
	}
	printf("%.6lf
",l);
	return 0;
}

H. lajiniunai的黑山羊

思路

贪心+带权并查集

首先贪心是很好想到的，将羊群按 (b) 的大小从大到小排序，从前到后依次决定每个羊的 (a) 值，如果当前 (a) 已有羊占用，就 (+1) 再看。当然这样的花费是最少的，但这样慢慢自加肯定会超时。

用带权并查集可以加速这个自加过程，将连续的用过的数合并到一个集合，如果遇到一个已经用过的数，可以通过并查集直接跳到这个数所在集合的末尾，然后计算花费。

代码

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e5+10;
typedef long long LL;
int T,n,fa[MAXN],siz[MAXN],minv[MAXN];
map<int,int> mp;
struct Pair{
	int a,b;
}p[MAXN];

bool cmp(Pair x,Pair y){
	return x.b>y.b;
}

int get(int x){
	if(x==fa[x]) return x;
	int root=get(fa[x]);
	minv[fa[x]]=min(minv[x],minv[fa[x]]);
	return fa[x]=root;
}

void merge(int x,int y){
	x=get(x),y=get(y);
	fa[x]=y;
	minv[y]=min(minv[x],minv[y]);
	siz[y]+=siz[x];
}

int main(){
	scanf("%d",&T);
	while(T--){
		mp.clear();
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%d%d",&p[i].a,&p[i].b);
		for(int i=1;i<=n;i++)
			fa[i]=i,siz[i]=1;
		sort(p+1,p+n+1,cmp);
		LL ans=0;
		for(int i=1;i<=n;i++){
			int num;
			if(!mp[p[i].a]){
				num=p[i].a;
			}
			else{
				int rt=get(mp[p[i].a]);
				num=minv[rt]+siz[rt];
				ans+=1ll*(num-p[i].a)*p[i].b;
			}
			mp[num]=i;
			minv[i]=num;
			if(mp[num-1]) merge(mp[num-1],i);
			if(mp[num+1]) merge(mp[num+1],i);
		}
		printf("%lld
",ans);
	}
	return 0;
}

未完待续……