[AtCoder Grand Contest 032] E Modulo Pairing（结论）

Problem

题目地址

Solution

结论1

• 最终答案一定存在一个分界点，满足：

其中蓝线表示 (x+y<M)，红线表示 (x+y >= M)。

证明

对于任意 (4) 个点 (a,b,c,d)，且满足 (a le b le c le d le M)

• 情况1： 假设其中任意两个相加小于 (M)，即对于 (a,b,c,d) 任意组合都满足条件 (x+y < M)。那么选择 ((a,d),(b,c)) 是最优的，即最大加最小，次大加次小。证明很容易：

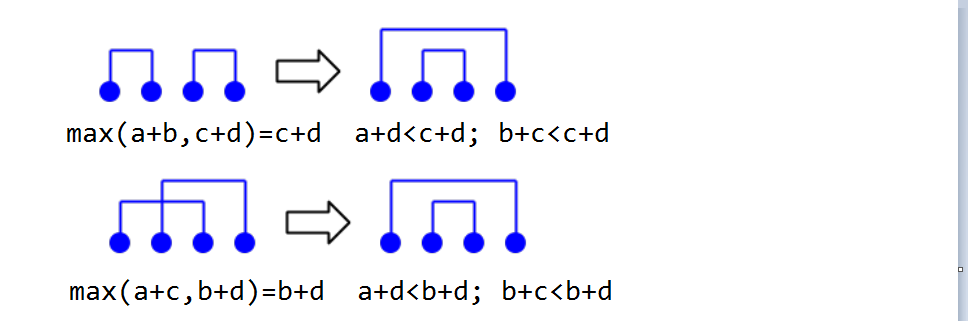
• 情况2： 假设其中任意两个相加大于 (M)，即对于 (a,b,c,d) 任意组合都满足条件 (x+y >= M)。那么选择 ((a,d),(b,c)) 是最优的，即最大加最小，次大加次小。因为不妨把 ((x+y)\%M) 写成 (x+y-M)，则证明和情况1是相同的。

• 情况3： 红线和蓝线覆盖或者交叉，那么 选择((a,b),(c,d)) 是最优的，而且一定满足 ((a,b)) 是蓝线，((c,d)) 是红线。证明如下：

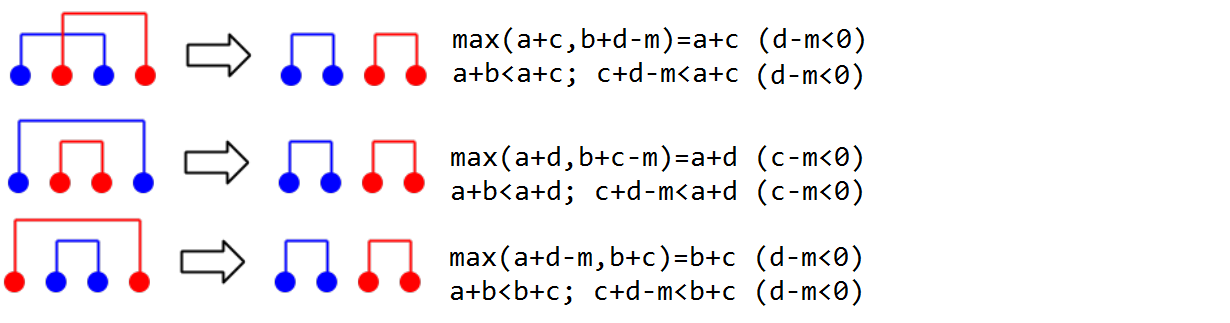
综上，如果红线和蓝线覆盖或者交叉，那么一定不是最终答案。反之，最终答案存在一个分界点，使得左部分全是蓝线，右部分全是红线。对于全是蓝线的一块，总是最大加最小，次大加次小最优，红线的一块同理。

结论2

• 在分界点合法的前提下，分界点的位置越小，答案越优。（分界点合法即为右半部分最大加最小，次大加次小......都大于等于 (M)）例如：

可以用类似的方法，分界点位置变小后，变化后蓝线的一块每个数的贡献都与变化前有一一对应的变小，红线的一块同理，从而证明。

题解

根据 结论1 和 结论2，我们可以二分合法且位置最小的分界点。时间复杂度 (O(n log n))

Code

Talk is cheap.Show me the code.

#include<bits/stdc++.h>
using namespace std;
inline int read() {
    int x = 0, f = 1; char ch = getchar();
    while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
    while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
    return x * f;
}
const int N = 2e5+7;
int n,m;
int a[N];
bool check(int lim) {
	int len = lim << 1;
	for(int i=len+1;i<=2*n;++i) {
		if(a[i]+a[2*n-i+len+1] < m) return false;
	}
	return true;
}
int main()
{
	n = read(), m = read();
	for(int i=1;i<=2*n;++i) a[i] = read();
	sort(a+1, a+1+2*n);
	int l = 0, r = n, mid, ans = n;
	while(l <= r) {
		mid = (l + r) >> 1;
		if(check(mid)) {
			ans = mid; r = mid - 1;
		} else l = mid + 1;
	}
	int len = ans << 1, ansval = 0;
	for(int i=1;i<=len;++i) {
		ansval = max(ansval, a[i]+a[len-i+1]);
	}
	for(int i=len+1;i<=2*n;++i) {
		ansval = max(ansval, a[i]+a[2*n-i+len+1]-m);
	}
	printf("%d
",ansval);
	//printf("%d
",check(0));
    return 0;
}
/*
2 10
1 9 1 9

0
*/

Summary

（部分图片摘自 Atcoder官方题解）

多做题！