Problem
Solution
-
考虑一个简化版问题:给定长度为 (m) 的字符串 (S),和一些模式串 (c_i),问有多少种方案拼成 (S)。
-
思路:设 (f[i]) 表示有多少种方案拼成 (S[1...i]),那么有转移 (f[i]=sum_{c_x=S[k...i]} f[k]),答案就是 (f[m])。具体的,看作有 (m+1) 个点,若 (c_x = S[k...i]),则在 (k->i) 连一条边,最统计有多少种从 (0) 到 (m) 的路径。
题解
设 (f[i,j]) 表示第 (i) 个字符串匹配了 (j) 位是否可达。
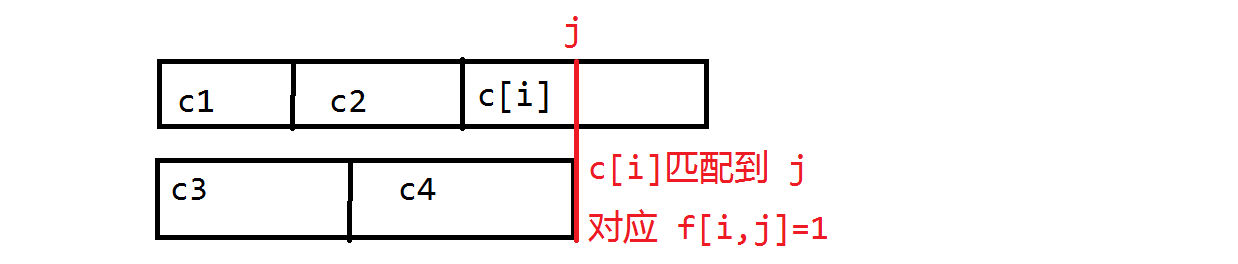
同样把 ((i,j)) 这个状态看成一个点。((i,j)->(u,v)) 之间有边则说明可以将 (c_u) 接上去,即满足:(S_i[j...len]=S_u[1...v])。
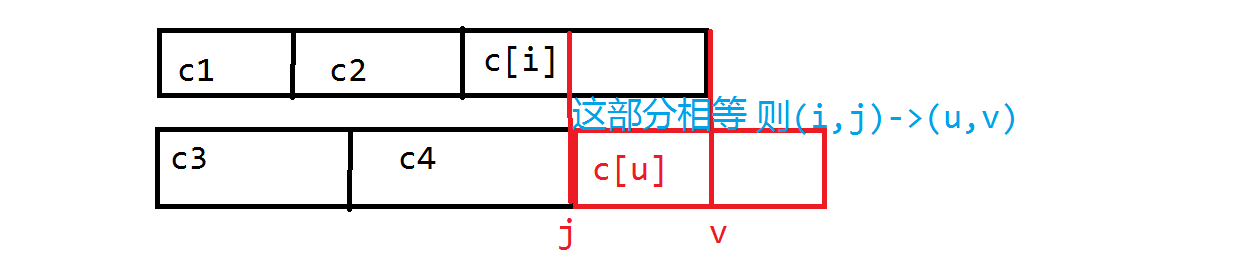
注意处理一些细节。初始状态 (f[i,0]=1),最终看是否有 (f[i,n]=1)。状态数 (O(nL)),建边复杂度 (O(n^2L^2)),时间复杂度 (O(n^2L^2))。
Code
Talk is cheap.Show me the code.
#include<bits/stdc++.h>
#define mp make_pair
#define fi first
#define se second
using namespace std;
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch<'0' || ch>'9') { if(ch=='-') f=-1; ch=getchar(); }
while(ch>='0'&&ch<='9') { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); }
return x * f;
}
typedef pair<int,int> PII;
const int N = 57, maxn = N*N;
int n,cnt;
int head[maxn];
int f[N][N];
char str[N][N];
struct Edge {
int next,to;
}edge[maxn*maxn];
inline void add(int u,int v) {
edge[++cnt] = (Edge)<%head[u],v%>;
head[u] = cnt;
}
bool check(int x,int lx,int y,int ly,int len) {
for(int i=0;i<len;++i)
if(str[x][lx+i] ^ str[y][ly+i]) return false;
return true;
}
int Getid(PII x) {
return x.fi*N + x.se;
}
PII Getpii(int x) {
return mp(x/N, x%N);
}
void work() {
memset(str, 0, sizeof(str));
memset(head, 0, sizeof(head)); cnt = 0;
memset(f, 0, sizeof(f));
n = read();
for(int i=1;i<=n;++i) scanf("%s",str[i]+1);
for(int i=1;i<=n;++i) {
int len = strlen(str[i]+1);
for(int j=0;j<=len;++j) {
for(int u=1;u<=n;++u) {
if(j==0 && i==u) continue;
int ulen = strlen(str[u]+1);
if(ulen >= len-j) {
if(check(i,j+1,u,1,len-j)) {
add(Getid(mp(i,j)), Getid(mp(u,len-j)));
}
} else {
if(check(i,j+1,u,1,ulen)) {
add(Getid(mp(i,j)), Getid(mp(i,j+ulen)));
}
}
}
}
}
queue<int> q;
for(int i=1;i<=n;++i) {
int len = strlen(str[i]+1);
q.push(Getid(mp(i,0)));
f[i][0] = 1;
}
while(!q.empty()) {
int u = q.front(); q.pop();
PII uu = Getpii(u); int x = uu.fi, y = uu.se;
for(int i=head[u];i;i=edge[i].next) {
int v = edge[i].to;
PII vv = Getpii(v); int nx = vv.fi, ny = vv.se;
if(!f[nx][ny]) {
f[nx][ny] = f[x][y]; q.push(v);
}
}
}
bool flag = 0;
for(int i=1;i<=n;++i) flag |= f[i][strlen(str[i]+1)];
if(flag) puts("No");
else puts("Yes");
}
int main()
{
int T = read();
while(T--) work();
return 0;
}
/*
1
2
00
000
No
*/