LOOPS
Time Limit: 5 Sec Memory Limit: 64 MB[Submit][Status][Discuss]
Description
Akemi Homura is a Mahou Shoujo (Puella Magi/Magical Girl).
Homura
wants to help her friend Madoka save the world. But because of the plot
of the Boss Incubator, she is trapped in a labyrinth called LOOPS.

The
planform of the LOOPS is a rectangle of R*C grids. There is a portal in
each grid except the exit grid. It costs Homura 2 magic power to use a
portal once. The portal in a grid G(r, c) will send Homura to the grid
below G (grid(r+1, c)), the grid on the right of G (grid(r, c+1)), or
even G itself at respective probability (How evil the Boss Incubator
is)!
At the beginning Homura is in the top left corner of the LOOPS
((1, 1)), and the exit of the labyrinth is in the bottom right corner
((R, C)). Given the probability of transmissions of each portal, your
task is help poor Homura calculate the EXPECT magic power she need to
escape from the LOOPS.
Input
The first line contains two integers R and C.
The
following R lines, each contains C*3 real numbers, at 2 decimal places.
Every three numbers make a group. The first, second and third number of
the cth group of line r represent the probability of transportation to
grid (r, c), grid (r, c+1), grid (r+1, c) of the portal in grid (r, c)
respectively. Two groups of numbers are separated by 4 spaces.
It
is ensured that the sum of three numbers in each group is 1, and the
second numbers of the rightmost groups are 0 (as there are no grids on
the right of them) while the third numbers of the downmost groups are 0
(as there are no grids below them).
You may ignore the last three numbers of the input data. They are printed just for looking neat.
Terminal at EOF
Output
A real number at 3 decimal places (round to), representing the expect magic power Homura need to escape from the LOOPS.
Sample Input
2 2
0.00 0.50 0.50 0.50 0.00 0.50
0.50 0.50 0.00 1.00 0.00 0.00
2 2
0.00 0.50 0.50 0.50 0.00 0.50
0.50 0.50 0.00 1.00 0.00 0.00
Sample Output
6.00
6.00
HINT
2 <= R, C <= 1000, 答案<=1000000.
Main idea
每个位置有三种情况:不动、向右走一步、向下走一步。给出了每种情况的概率,执行一次情况会产生2的贡献,询问从 (1,1) 到 (n,m)的贡献的期望。多组数据。
Solution
我们运用期望DP求解,我们先令 f[i][j] 表示从(n,m) 到 (i,j) 的期望,然后可以轻易地推出一个式子,左右移项一下即可:
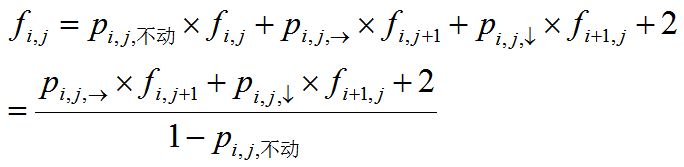
得到了这个式子之后我们就可以从 (n,m) 递推到 (1,1) 了。
Code

1 #include<iostream>
2 #include<string>
3 #include<algorithm>
4 #include<cstdio>
5 #include<cstring>
6 #include<cstdlib>
7 #include<cmath>
8 #include<bitset>
9 using namespace std;
10 const int ONE = 1001;
11
12 int n,m;
13 double p[ONE][ONE][3],f[ONE][ONE];
14
15 int get()
16 {
17 int res=1,Q=1; char c;
18 while( (c=getchar())<48 || c>57)
19 if(c=='-')Q=-1;
20 if(Q) res=c-48;
21 while((c=getchar())>=48 && c<=57)
22 res=res*10+c-48;
23 return res*Q;
24 }
25
26 int main()
27 {
28 while(scanf("%d%d", &n, &m) != EOF)
29 {
30 for(int i=1;i<=n;i++)
31 for(int j=1;j<=m;j++)
32 scanf("%lf %lf %lf", &p[i][j][0], &p[i][j][1], &p[i][j][2]);
33
34 f[n][m] = 0;
35 for(int i=n;i>=1;i--)
36 for(int j=m;j>=1;j--)
37 if(p[i][j][0]!=1 && (i!=n || j!=m))
38 f[i][j] = (p[i][j][1]*f[i][j+1] + p[i][j][2]*f[i+1][j] + 2) / (1-p[i][j][0]);
39
40 printf("%.3lf
",f[1][1]);
41 }
42 }
