【数据结构】【植树计划】哈夫曼树Huffman Tree[CF]D. Boxes And Balls
前置知识:
二叉树叶子结点与度为2的节点关系
在二叉树中,一个结点最多拥有两个儿子结点,因而结点的类型可以分为拥有0个儿子结点的结点(n_0),拥有1个儿子结点的结点(n_1)和拥有2个儿子结点的结点(n_2),记总结点个数为S
注意:显然,根结点不是任何结点的子结点
所以有,总儿子结点个数=总结点数-1,记为(S_{0}=S-1)
换种角度出发,从儿子结点个数是如何产生的角度来看,有
(S-1=S_{0}=0 imes n_{0}+1 imes n_{1}+2 imes n_{2}=n_{1}+2n_{2})
即有
(S=n_{1}+2n_{2}+1)
(n_{0}=n_{2}+1)
而一个结点没有儿子结点,就是说这个结点的度为0,也就是所谓的儿子结点。
所以在一颗二叉树中,叶子结点的个数等于入度为2的结点的个数再加上1.
定义:
WPL
设二叉树具有n个带权值的叶结点,那么从根节点到各个叶节点的路径长度与相应结点权值的乘积的和,叫做二叉树的带权路径长度WPL(Weighted Path Length)
- WPL相当于所有的点的点权乘上层数的和
WPL的计算
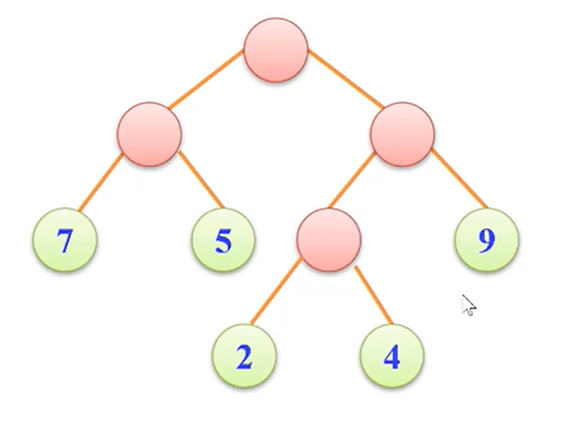
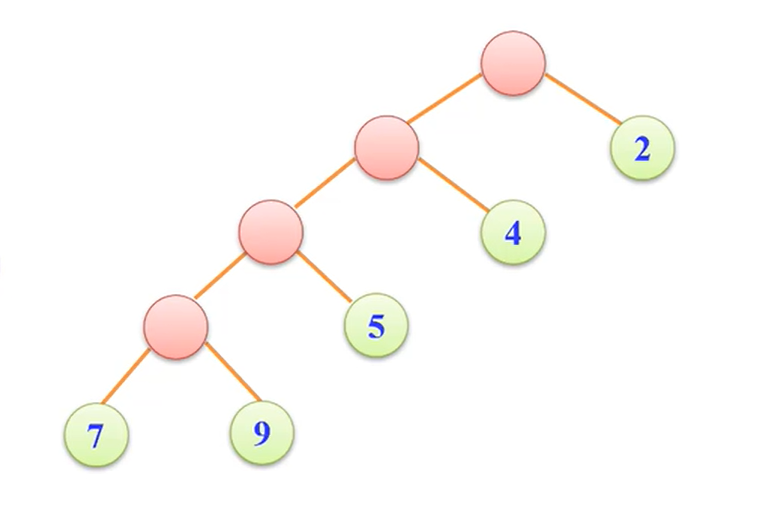
经观察可得要使得WPL的大小越小有两种方法,一是压缩路径(减少层数),二是把越大的数越安排到层数比较小的位置。
而总有一种安排方法会使得WPL值达到最小,而这个时候形成的图形,而就是所谓的哈夫曼树
哈夫曼树
哈夫曼树的定义
- 哈夫曼树:拥有最小带权路径长度的二叉树称为哈夫曼树(也称作最优树)
哈夫曼树的原则
- 权值越大的结点越靠近根结点
- 权值越小的结点越远离根结点
换种角度来看,可以将结点离根结点的距离理解成是结点所处在层数。
哈夫曼树的构造流程
给定一些数,将其从小到大进行排序,得到序列(a_{1},a_{2},....,a_{n})
Step1:取出点权最小的两个的结点(a_{1},a_{2}),将(a_{1},a_{2})进行合并,这个时候会生成一个点权等于这两点的点权和的点,记为(b_{1})。
Step2:向取出了两个个元素的序列中加入(b_{1}),并进行排序(这里涉及到时间复杂度的问题,优先队列的单次排序是log级别的)
Step3:重复Step1和Step2的操作,直至序列中只剩下一个元素。
哈夫曼树的叶结点个数(n_{0})和结点数(S)的关系
注意:根据哈夫曼树的构造流程,我们可以明显发现,哈夫曼树中并不存在子结点个数为1的结点。
所以有,(S=n_{0}+n_{2})
且在前置知识的帮助下,我们有这样的普适的结论(n_{0}=n_{2}+1)
于是,我们有(S=2n_{0}-1)
哈夫曼编码
k叉哈夫曼树
与一般的哈夫曼树不同的是k叉哈夫曼树的构造流程是k叉哈夫曼树每次提取的是前k个小的数字来进行合并。

哈夫曼树的叶结点个数(n_{0})和结点数(S)的关系,戳我
(n_0=(k-1) imes n_{k}Rightarrow (k-1)|n_0),若叶子个点个数有机会被k-1整除的话,这可以搭建出k叉哈夫曼树。
题目的k存在两种取值的k,一种为2(k-1=1所以,不用取考虑2这种情况),而另一种k的取值为3(需单独考虑叶子结点个数能否会被2整除掉,若可以,非常好,若不可以,再向条件中补一个0,凑成偶数)。
代码
#include <bits/stdc++.h>
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define pi acos(-1.0)
#define PII pair<int,int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define ull unsigned long long
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define MAX 1000005
#define MOD 1000000007
#define INF 0x3f3f3f3f
#define lowbit(x) (x&-x)
using namespace std;
int n,m;
int main()
{
scanf("%d",&n);
ll ans=0,x;
priority_queue<ll,vector<ll>,greater<ll> > pq;
repd(i,1,n)
{
scanf("%lld",&x);
pq.push(x);
}
if(n%2==0)pq.push(0);
while(pq.size()>1)
{
x=pq.top();pq.pop();
x+=pq.top();pq.pop();
x+=pq.top();pq.pop();
pq.push(x);
ans+=x;
}
printf("%lld",ans);
return 0;
}