

题解:我们记b、c数组分别表示左右、上下的移动,左-右+,上+下-,如果某2点b、c分别相等,即回到了原地,ans++即可。
对于最后的20%数据,只有左右,我们记录b出现的次数cnt,算出有多少个点在移动过程中走到了相同的位置,ans+=cnt*(cnt-1)/2即可。
PS:①这题虽然相当裸,但是最后一个点爆int,所以我们要开long long存QAQ;②初始的位置0也要考虑。
代码如下:
1 #include<cstdio> 2 #include<iostream> 3 #define Max 400005 4 using namespace std; 5 long long n,b[Max],c[Max],cnt1[Max],cnt2[Max],ans; 6 char a[Max]; 7 bool flag; 8 void work(int x){ 9 if(x>=0) cnt1[x]++; 10 else cnt2[-x]++; 11 } 12 int main() 13 { 14 freopen("command.in","r",stdin); 15 freopen("command.out","w",stdout); 16 scanf("%lld ",&n); cnt1[0]++; 17 for(int i=1;i<=n;i++){ 18 scanf("%c",&a[i]); 19 b[i]=b[i-1]; c[i]=c[i-1]; 20 if(a[i]=='U') c[i]++,flag=true; 21 if(a[i]=='D') c[i]--,flag=true; 22 if(a[i]=='L') b[i]--,work(b[i]); 23 if(a[i]=='R') b[i]++,work(b[i]); 24 } 25 if(!flag){ 26 for(int i=0;i<=n;i++){ 27 ans+=cnt1[i]*(cnt1[i]-1)/2; 28 ans+=cnt2[i]*(cnt2[i]-1)/2; 29 } 30 printf("%lld",ans); 31 return 0; 32 } 33 for(int i=0;i<n;i++) 34 for(int j=i+1;j<=n;j++) 35 if(b[i]==b[j]&&c[i]==c[j]) ans++; 36 printf("%lld",ans); 37 return 0; 38 }
------------------------------------------------------------华丽的分割线----------------------------------------------------------------------

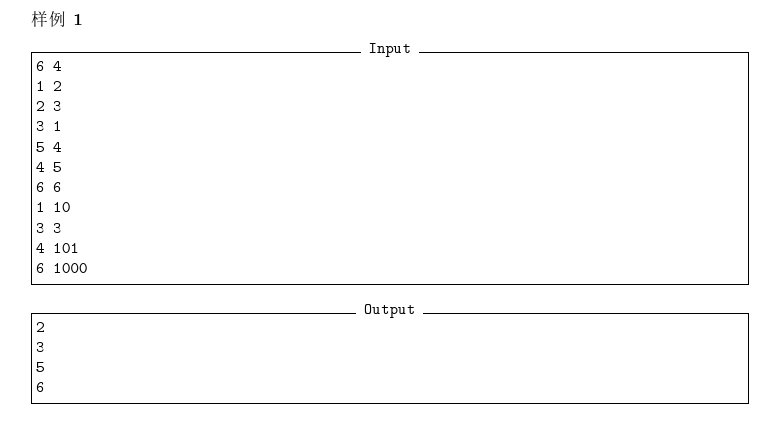
题解:由题意,我们把相互指向的桌子连起来,就是一张由数个环组成的有向图,我们就可以预处理出每个点所在环的长度xh,搜索时把距离模xh再搜即可。
代码如下:
1 #include<cstdio> 2 #include<iostream> 3 #define Max 100005 4 using namespace std; 5 int n,Q,a[Max],b[Max]; 6 int now[Max],to[Max],xh[Max],cnt; 7 bool vis[Max]; 8 void dfs(int x){ 9 if(vis[x]) return; 10 vis[x]=true; cnt++; 11 dfs(to[x]); 12 xh[x]=cnt; 13 } 14 int find(int x,int y){ 15 if(y==0) return x; 16 return find(to[x],y-1); 17 } 18 int main() 19 { 20 freopen("position.in","r",stdin); 21 freopen("position.out","w",stdout); 22 scanf("%d%d",&n,&Q); 23 for(int i=1;i<=n;i++){ 24 scanf("%d%d",&a[i],&b[i]); 25 now[a[i]]=i; 26 } 27 for(int i=1;i<=n;i++) to[i]=now[b[i]]; 28 for(int i=1;i<=n;i++) 29 if(!vis[i]){cnt=0; dfs(i);} 30 for(int i=1;i<=Q;i++){ 31 int x,y; scanf("%d%d",&x,&y); 32 y%=xh[x]; 33 printf("%d ",find(x,y)); 34 } 35 return 0; 36 }