


题解:这道题是数学题,横、竖分2种情况,然后解方程即可。
①横切:我们发现每次切掉三角形下方的梯形后,新三角形的形状和原来相同,所以我们求设高为b的等腰三角形切掉底部1/n面积的梯形的高x,就是我们每次切的位置了,最后求得x=b-b*sqrt(1-1/n)。
②竖切:我们先分2种情况,若分成偶数部分,则中间要切一刀,否则中间不切,然后因为左右割痕对称,我们就求左侧一个底为a/2的直角三角形切掉左侧整个等腰三角形面积的cnt/n面积的直角三角形的底x即可,最后求得x=a*sqrt(cnt/2*n)。
代码如下:
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 int n,c; 6 double a,b,ans,cnt,ans1[1001]; 7 int main() 8 { 9 freopen("cut.in","r",stdin); 10 freopen("cut.out","w",stdout); 11 scanf("%d%lf%lf%d",&n,&a,&b,&c); 12 if(c==0){ 13 cnt=n; 14 for(int i=1;i<n;i++){ 15 double bb=b-ans; 16 ans+=(bb-bb*sqrt(1-1/(cnt--))); 17 printf("%.10lf ",ans); 18 } 19 return 0; 20 } 21 else{ 22 int i; 23 for(i=1;i<=(n-1)/2;i++){ 24 ans1[i]=(a*sqrt(i/(double)(2*n))); 25 printf("%.10lf ",ans1[i]); 26 } 27 if(n%2==0) printf("%.1lf ",a/2),i++; 28 for(i;i<n;i++) 29 printf("%.10lf ",a-ans1[n-i]); 30 return 0; 31 } 32 }
-----------------------------------------------------------------华丽的分割线------------------------------------------------------------------------
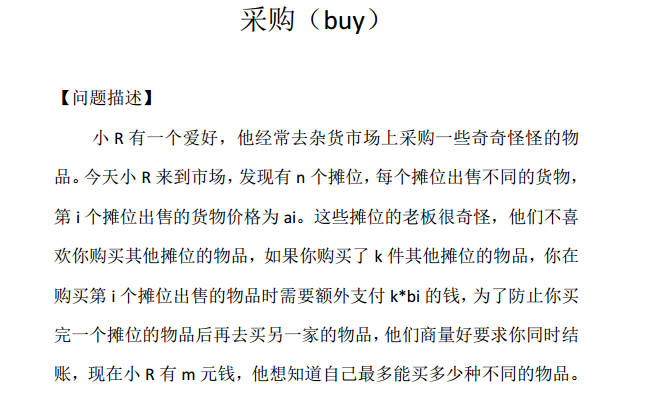


题解:这道题麻烦的地方在于若新添加一个新的商品,所有已选的商品b都要乘当前已购买数目x-1,于是刘Jimmy大佬(orz orz orz)就想到二分答案,如果确定了购买数目,则我们记一个sum数组,存a[i]+b[i]*(x-1)的值,然后从小到大sort,取最小的x个即可。
代码如下:
1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #define MN 100005 5 using namespace std; 6 long long n,m,b[MN],sum[MN],a[MN]; 7 int main() 8 { 9 freopen("buy.in","r",stdin); 10 freopen("buy.out","w",stdout); 11 scanf("%lld%lld",&n,&m); 12 for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i],&b[i]); 13 int l=0,r=n; 14 while(l<=r){ 15 int mid=(l+r)>>1; 16 for(int i=1;i<=n;i++) sum[i]=a[i]+(mid-1)*b[i]; 17 sort(sum+1,sum+n+1); 18 long long tot=0; 19 for(int i=1;i<=mid;i++) tot+=sum[i]; 20 if(tot>m) r=mid-1; 21 else l=mid+1; 22 } 23 printf("%d",l-1); 24 return 0; 25 }
-----------------------------------------------------------------华丽的分割线------------------------------------------------------------------------



代码如下:
1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 int n,num[10005],f[10005]; 5 long long ans; 6 bool vis[10005]; 7 int main() 8 { 9 scanf("%d",&n); 10 for(int i=1;i<=n;i++){ 11 int x; scanf("%d",&x); 12 f[i]=num[i]=num[i-1]^x; 13 } 14 for(int i=1;i<=n;i++){ 15 int best=0; 16 for(int j=1;j<=n;j++) 17 if(!vis[j]&&(!best||f[j]<f[best])) best=j; 18 vis[best]=1; ans+=f[best]; 19 for(int j=1;j<=n;j++) 20 if(!vis[j]) f[j]=min(f[j],num[j]^num[best]); 21 } 22 printf("%lld",ans); 23 return 0; 24 }