leetcode 319 29

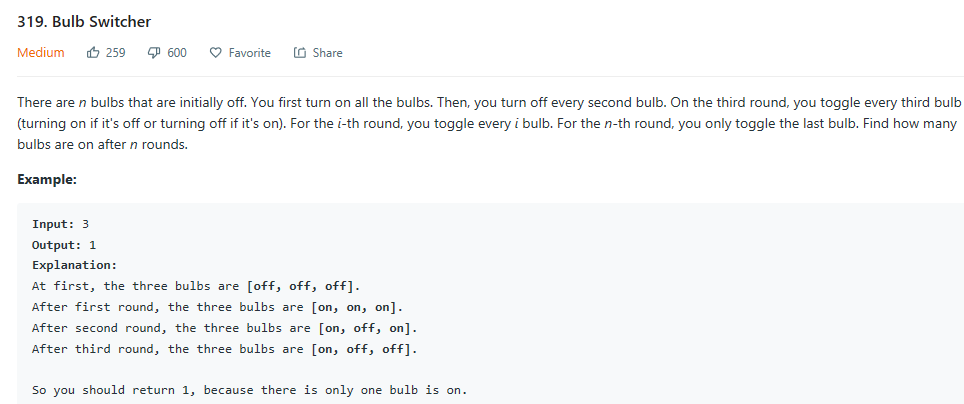
题意：n个灯泡，第一轮全部打开；第二轮每隔2k（k=0，1，...n）个（偶数2，4，6，8.....）关闭；第三轮3k（3，6，9，12,....）个打开；... 以此类推

所以当操作为奇数个时，灯是开的。而只有平方数的乘积个数为奇数。可以用sqrt(n)得到有1-n中多少个完全平方数。

class Solution {
public:
    int bulbSwitch(int n) {
        return sqrt(n);
    }
};

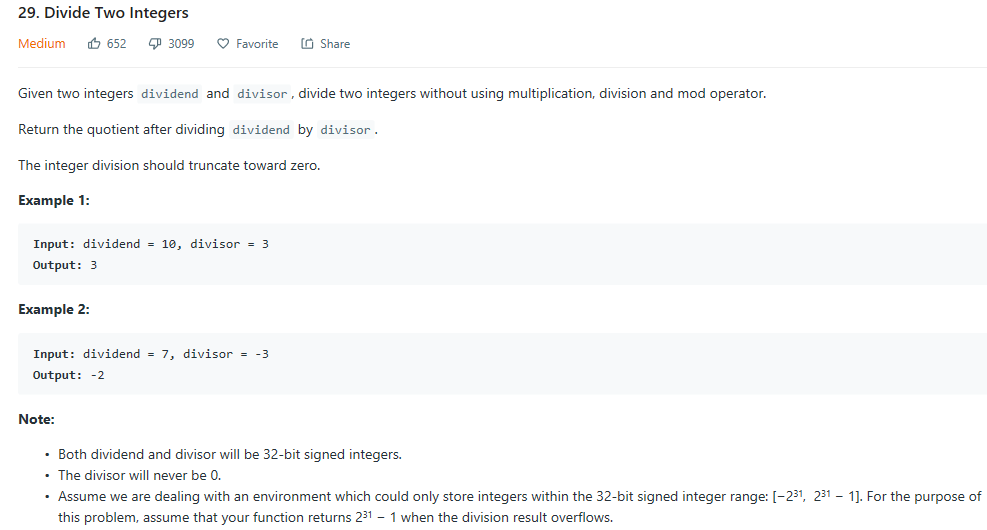
题意：两个32位的有符号整数，取值范围为[−2³¹,  2³¹ − 1]。求被除数（dividend）和除数(divisor)相除得到的整数的值。不能使用除法，乘法和求余操作。

思路：使用移位运算（左移一位相当于 乘2）将divisor逐一乘2来逼近dividend。

Suppose dividend = 15 and divisor = 3, 15 - 3 > 0. We now try to subtract more by shifting 3 to the left by 1 bit (6). Since 15 - 6 > 0, shift 6 again to 12. Now 15 - 12 > 0, shift 12 again to 24, which is larger than 15. So we can at most subtract 12 from 15. Since 12 is obtained by shifting 3 to left twice, it is 1 << 2 = 4 times of 3. We add 4 to an answer variable (initialized to be 0). The above process is like 15 = 3 * 4 + 3. We now get part of the quotient (4), with a remaining dividend 3.

Then we repeat the above process by subtracting divisor = 3 from the remaining dividend = 3 and obtain 0. We are done. In this case, no shift happens. We simply add 1 << 0 = 1 to the answer variable.

特殊情况：dividend = INT_MIN and divisor = -1, 即当被除数是−231 ，除数是-1时，得到的结果为231，超出了int的范围，此时应返回INT_MAX。

1）labs(long n)             //回长整型参数n的绝对值

2）条件 ？a : b          // 若条件为真，结果为a,  为假，结果为b

3）^符号表示：按位异或运算符。
参与运算的两个值，如果两个相应位相同，则结果为0，否则为1。即：0^0=0， 1^0=1， 0^1=1， 1^1=0

注意：m，n的类型不能定义为int，因为当dividend和divisor为−2³¹时，绝对值后会超出整型的范围，所以要将m和n定义为long。

class Solution {
public:
    int divide(int dividend, int divisor) {
        if(dividend==INT_MIN && divisor==-1) 
            return INT_MAX;       
        else{
            long m = labs(dividend), n = labs(divisor), res = 0;
            int sign = (dividend < 0)^(divisor<0)? -1:1 ;
            if(n==1) return sign ==1 ? m:-m;
            while(m>=n){
                long t = n, p = 1;
                while(m>= (t<<1)){
                    t <<= 1;
                    p <<= 1;
                }
                res += p;
                m -= t;
            }
            return sign==1? res: -res;
            }
    }
};