位运算、快速幂

 位运算：

快速幂： 

例1. a^b%p

题目链接：https://www.acwing.com/problem/content/91/

 

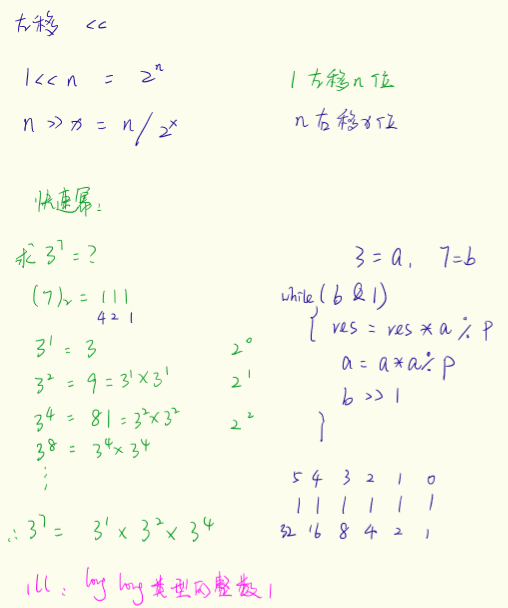
#include<iostream>
using namespace std;
int main(){
    int a, b, p;
    cin>> a >> b >> p;
    int res = 1 % p;   //若b=0时，不会进入while循环,故res要先模p
    while(b){
        if(b&1)
        //若b的个位为1
            res = res * 1ll * a % p;  //1ll是将res转化为长整型
            a = a * 1ll * a % p;
            b >>= 1;
    }
    cout<<res<<endl;
    return 0;
}

例2.  a*b%p

https://www.acwing.com/problem/content/92/

两个10^18的数相乘是溢出的，但是相加是不溢出的。

 

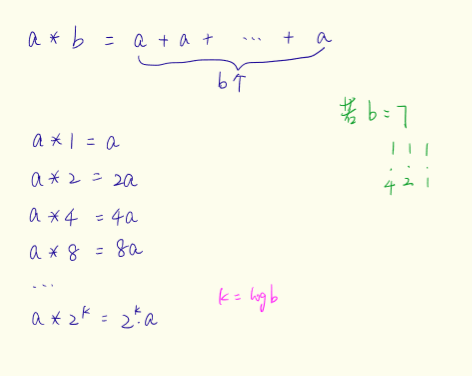
#include<iostream>
using namespace std;
typedef unsigned long long ull;

int main(){
    ull a, b, p;
    cin>>a>>b>>p;
    ull res = 0;
    while(b){
        if(b&1)
            res = (res + a)%p;
        a = (a+a)%p;
        b = b>>1;
    }
    cout<< res << endl;
    return 0;
}

例3.旅行商问题

https://www.acwing.com/problem/content/93/

思路：

假设四个点：0,1,2,3

有两条路径：0 -> 1 -> 2 -> 3  (最短距离为18)

和 0 -> 2 -> 1 -> 3   （20）

 

两个关键要素：

1）哪些点被用过；

2）目前停在哪个点上。

用 f[state][j] 来表示 state：当前哪个点被用过（是个集合）；j：停在哪个点上。

若从k点转移过来：f[state][j] = f[state_k][k] + weight[k][j]，state_k 是 state 除掉 j 之后的集合，且 state_k 要包含 k。

用位运算来表示state这个集合，即用一个二进制整数来表示state。(状态压缩：用0表示这个点不存在，1表示这个点存在)。这里1<=n<=20 所以用20位二进制来表示state。

如：0, 1, 4 用二进制表示状态为：

state = 10011

索引： 43210

注意：一般会将大数组定义为全局变量或静态变量（在堆空间），因为main()函数里C++默认是栈空间（默认为4M）。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 20, M = 1<<20;   //左移20, 相当于乘上2^20
int n;
int f[M][N], weight[N][N];
int main(){
    cin>>n;
    for(int i=0; i<n; i++)
        for(int j=0; j<n; j++)
            cin>>weight[i][j];
    
    memset(f, 0x3f, sizeof(f));  //初始化f里的所有状态为正无穷
    f[1][0] = 0;   //最开始在0号点，故状态集合内只包含0号点, 还没有走过任何路程，故初始化为0
    
    for(int i=0; i<1<<n; i++){
        for(int j=0; j<n; j++){
            if(i>>j & 1){
                //判断i的第j位是不是1：将i右移j位和1相与
                for(int k=0; k<n; k++){
                    if(i-(1<<j) >>k & 1)
                        //把当前状态的第j位减去，再判断第k位是否为1，减法优先级比移位操作符高
                        f[i][j] = min(f[i][j], f[i-(1<<j)][k] + weight[k][j]);
                }
            } 
            
        }
    }
    cout<<f[(1<<n)-1][n-1] <<endl;
    return 0;
}

异或：

1. 可以帮助我们实现成对的思想。

比如：0，1

2，3

4，5

6，7

异或1 : 可以帮助我们得到一对里的一个配偶。

0^1 = 1, 1^1 = 0

4^1 = 5, 5^1 = 4

2. lowbit 运算：求一个数（二进制下）从后向前数直到遇到第一个’1’时的数 

lowbit(1110010000) = 10000

如 ： 取反 ： 0001101111 

加1：0001110000

(取反加1相当于取 1110010000的补码) ，将 1110010000 & 0001110000 就得到 10000

int lowbit(n)

{

　　return (~n+1) &n;       // return (-n) & n;