zoukankan html css js c++ java

斜率优化DP

从lyd蓝书入的门。

一、任务安排1

这是最弱化的板子。

首先考虑O(n³)的DP：

f[i][j]=min_0<=k<i([f[k][j-1]+(S*J+sumT[i])*(sumC[i]-sumC[k]));

考虑优化：因为没有限制要分成多少批，而我们之所以多设一维j是因为我们需要知道启动了多少次，从而计算时间。

这里运用到一种“费用提前计算”的思想来优化：

在DP过程中我们并不容易直接求出每批任务的完成时刻，而我们可以考虑每启动一次就会对之后所有的任务产生影响，

所以我们可以先把费用累加进来，就可以实现O(n²)的DP：

f[i]=min_0<=j<i{f[j]+sumT[i]*(sumC[i]-sumC[j])+S*(sumC[N]-sumC[j])};

#include<bits/stdc++.h>
#define RG register
#define IL inline
#define LL long long
using namespace std;

IL int gi () {
    RG int x=0,w=0; char ch=0;
    while (ch<'0'||ch>'9') {if (ch=='-') w=1;ch=getchar();}
    while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return w?-x:x;
}

const int N=1e5+10;

int n,S,T[N],C[N];
LL f[N],preT[N],preC[N];

int main ()
{
    RG int i,j;
    n=gi(),S=gi();
    for (i=1;i<=n;++i)
        T[i]=gi(),C[i]=gi(),preT[i]=preT[i-1]+T[i],preC[i]=preC[i-1]+C[i];
    memset(f,0x3f,sizeof(f));
    f[0]=0;
    for (i=1;i<=n;++i)
        for (j=0;j<i;++j) f[i]=min(f[i],f[j]+preT[i]*(preC[i]-preC[j])+S*(preC[n]-preC[j]));
    printf("%lld
",f[n]);
    return 0;
}

BY BHLLX

二、任务安排2

N<=10⁵。。

n方DP过不了，我们需要继续优化。

把DP式子拆开：

f[i]=min{f[j]-(S+sumT[i])*sumC[j]}+sumT[i]*sumC[i]+S*sumC[N];

即把仅与i相关的，仅与j相关的，和i*j的乘积向分离出来。

然后移项可得：

f[j]=(S+sumT[i])*sumC[j]+f[i]-sumT[i]*sumC[i]-S*sumC[N];

容易发现与i相关的都是常量。

所以可以看成一个以sumC[j]为x，f[j]为y的一次函数。

现在我们要得到最小的i，就相当于在这些点上找到一个点，

使得斜率恒为(S+sumT[i])的直线的纵截距最小。

所以我们可以用单调队列维护一个下凸壳。

注意到最优的点肯定是左侧线段的斜率比k小，右侧的线段斜率比k大，且此题的k是单调递增的。

所以我们可以只需维护斜率大于k的部分，每次取最左端点即可。

至于单调队列的掐头和去尾操作：

在这个题目中，

掐头：目的是去掉超出范围的。若队头的斜率已经小于等于当前的k，去掉。

去尾：目的是去掉不可能成为答案的。若加入新的点后，不满足单调性。去掉。

#include <queue>
#include <cstdio>
#include <cstring>
#define RG register
#define IL inline
#define LL long long
using namespace std;

IL int gi () {
    RG int x=0,w=0; char ch=0;
    while (ch<'0'||ch>'9') {if (ch=='-') w=1;ch=getchar();}
    while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return w?-x:x;
}

const int N=1e5+10;

int n,L,R,T[N],C[N],q[N];
LL nowk,S,f[N],preT[N],preC[N];

int main ()
{
    RG int i;
    n=gi(),S=gi();
    for (i=1;i<=n;++i)
        T[i]=gi(),C[i]=gi(),preT[i]=preT[i-1]+T[i],preC[i]=preC[i-1]+C[i];
    memset(f,0x3f,sizeof(f));
    L=1,R=1,q[1]=0,f[0]=0;
    for (i=1;i<=n;++i) {
        //for (j=0;j<i;++j) f[i]=min(f[i],f[j]+preT[i]*(preC[i]-preC[j])+S*(preC[n]-preC[j]));        
        //f[j]=(preT[i]+S)*preC[j]+f[i]-preT[i]*preC[i]-S*preC[n]
        nowk=preT[i]+S;
        while (L<R&&nowk*(preC[q[L+1]]-preC[q[L]])>=(f[q[L+1]]-f[q[L]])) ++L;
        f[i]=f[q[L]]+preT[i]*preC[i]+S*preC[n]-nowk*preC[q[L]];
        while (L<R&&(f[i]-f[q[R]])*(preC[q[R]]-preC[q[R-1]])<=(f[q[R]]-f[q[R-1]])*(preC[i]-preC[q[R]])) --R;
        q[++R]=i;
    }
    printf("%lld
",f[n]);
    return 0;
}

BY BHLLX

三、任务安排3

与任务2的区别是：T可能为负数。

这意味着k不再具有单调性。

所以我们不能只保留大于k的部分凸壳，而应该保留整个凸壳。

所以就没有掐头操作，而且队头也不一定是最优的。

所以我们每次就要二分查找最优点，其他大致不变。

#include <queue>
#include <cstdio>
#include <cstring>
#define RG register
#define IL inline
#define LL long long
using namespace std;

IL int gi () {
    RG int x=0,w=0; char ch=0;
    while (ch<'0'||ch>'9') {if (ch=='-') w=1;ch=getchar();}
    while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return w?-x:x;
}

const int N=3e5+10;

int n,L,R,T[N],C[N],q[N];
LL nowk,S,f[N],preT[N],preC[N];

IL int search(int id,int k) {
    if (L==R) return q[L];
    int l=1,r=R,mid;
    while (l<r) {
        mid=l+r>>1;
        if (k*(preC[q[mid+1]]-preC[q[mid]])<(f[q[mid+1]]-f[q[mid]])) r=mid;
        else l=mid+1;
    }
    return q[r];
}

int main ()
{
    // T可以为负 preT不具有单调性 ∴斜率不具有单调性
    // 不能只维护下凸壳的部分 而是全部
    // 二分找最优
    RG int i,now;
    n=gi(),S=gi();
    for (i=1;i<=n;++i)
        T[i]=gi(),C[i]=gi(),preT[i]=preT[i-1]+T[i],preC[i]=preC[i-1]+C[i];
    memset(f,0x3f,sizeof(f));
    L=1,R=1,q[1]=0,f[0]=0;
    for (i=1;i<=n;++i) {
        //for (j=0;j<i;++j) f[i]=min(f[i],f[j]+preT[i]*(preC[i]-preC[j])+S*(preC[n]-preC[j]));        
        //f[j]=(preT[i]+S)*preC[j]+f[i]-preT[i]*preC[i]-S*preC[n]
        //while (L<R&&nowk*(preC[q[L+1]]-preC[q[L]])>=(f[q[L+1]]-f[q[L]])) ++L;        
        nowk=preT[i]+S,now=search(i,nowk);
        f[i]=f[now]+preT[i]*preC[i]+S*preC[n]-nowk*preC[now];
        while (L<R&&(f[i]-f[q[R]])*(preC[q[R]]-preC[q[R-1]])<=(f[q[R]]-f[q[R-1]])*(preC[i]-preC[q[R]])) --R;
        q[++R]=i;
    }
    printf("%lld
",f[n]);
    return 0;
}

BY BHLLX

四、CF311B

首先令A[i]=T[i]-ΣD[j],1<=j<=H[i]。要接到猫i则必须在A[i]后出发。

若出发时刻为T，则这只猫需等待的时间为T-A[i]。

把A排序，容易发现连续抱一段猫肯定比零散的抱猫优秀。

那么设f[i][j]表示i个人，已经接了j只猫。

f[i][j]=min{f[i-1][k]+A[j]*(j-k)+sumA[k]-sumA[j]}

同样的变形得：

f[i-1][k]+sumA[k]=A[j]*k+f[i][j]-Aj*j+sumA[j]

所以可以看成以k为x，f[i-1][k]+sumA[k]为y的一次函数。

因为A[j]单调，所以直接按任务安排2的方法做就好了。

#include<bits/stdc++.h>
#define RG register
#define IL inline
#define LL long long
#define DB double 
using namespace std;

IL int gi() {
    RG int x=0,w=0; char ch=0;
    while (ch<'0'||ch>'9') {if (ch=='-') w=1;ch=getchar();}
    while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
    return w?-x:x;
}

const int N=1e5+10;

int n,m,p,H,T,d[N],h[N],t[N];
LL q[N],A[N],sumD[N],sumA[N],f[110][N];

IL DB Slope(int id,int x,int y) {return 1.0*(f[id][x]+sumA[x]-f[id][y]-sumA[y])/(x-y);}

int main ()
{
    RG int i,j;
    n=gi(),m=gi(),p=gi();
    for (i=2;i<=n;++i) d[i]=gi(),sumD[i]=sumD[i-1]+d[i];
    for (i=1;i<=m;++i) h[i]=gi(),t[i]=gi(),A[i]=t[i]-sumD[h[i]];
    for (i=1;i<=m;++i) sumA[i]=sumA[i-1]+A[i];
    sort(A+1,A+m+1);
    memset(f,0x3f,sizeof(f));
    for (i=1,f[0][0]=0;i<=p;++i) {
        H=T=1,q[1]=0;
        for (j=1;j<=m;++j) {
            //f[i][j]=min(f[i][j],f[i-1][k]+(j-k)*A[j]-sumA[j]+sumA[k]);
            //f[i-1][k]+sumA[k]=A[j]*k+f[i][j]-Aj*j+sumA[j];
            while (H<T&&(DB)A[j]>=Slope(i-1,q[H+1],q[H])) ++H;
            f[i][j]=f[i-1][q[H]]+sumA[q[H]]+A[j]*(j-q[H])-sumA[j];
            while (H<T&&Slope(i-1,j,q[T])<=Slope(i-1,q[T],q[T-1])) --T;
            q[++T]=j;
        }
    }
    printf("%lld
",f[p][m]);
    return 0;
}

BY BHLLX

五、K-Anonymous Sequence

首先得把题目转化为：
把一个递增数列分成若干组，每组至少k个，每组的花费是这组的数字和减去最小值乘这组的总个数。求最小总花费。

那么我们可以设出n方DP：

f[i]=min{f[j]+(sum[i]-sum[j])-a[j+1]*(i-j)};

发现题中存在i和j的乘积项，考虑斜率优化。

但是我们又发现这个乘积项是i*a[j+1]，感觉很不好。

所以我们考虑把序列变成从大到小排序的。

那么，新的DP方程为：

f[i]=min(f[j]+(sum[i]-sum[j])-a[i]*(i-j))。

这时候我们发现乘积项就变成了a[i]*j，爽。

那么进行变形得：

f[j]-sum[j]=-a[i]*j+a[i]*i+f[i]-sum[i]。

注意到-a[i]单调递增且求最小值，所以仍然是维护下凸壳。

另，这个题有一个K的限制，所以需要延迟加入决策点。

#include<algorithm>
#include<cstring>
#include<cstdio>
#define IL inline
#define DB double
#define LL long long
using namespace std;
 
const int N=5e5+10;

LL a[N],f[N],s[N];
int n,K,T,q[N];
 
IL bool cmp(int a,int b) {return a>b;}

DB slope(int x,int y) {return (DB)((f[y]-s[y])-(f[x]-s[x]))/(DB)(y-x);}

int main() {
    scanf("%d",&T);
    while (T--) {
        scanf("%d%d",&n,&K);
        for (int i=1;i<=n;i++) scanf("%lld",&a[i]);
        sort(a+1,a+1+n,cmp);
        for (int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
        memset(f,0x3f,sizeof(f));
        int l=1,r=1;q[1]=0,f[0]=0;
        for (int i=K;i<=n;i++) {
            while (l<r&&slope(q[l],q[l+1])<=-a[i]) l++;
            f[i]=f[q[l]]+s[i]-s[q[l]]-a[i]*(i-q[l]);
            while (l<r&&slope(q[r-1],q[r])>=slope(q[r],i-K+1)) r--;
            q[++r]=i-K+1;
        }
        printf("%lld
",f[n]);
    }
    return 0;
}

BY BHLLX

总结（个人YY）：

对于DP方程中出现了i，j的乘积项的多考虑斜率优化。

斜率单调保留部分凸壳，不单调保留全部凸壳&&二分查找最优。

对于用单调队列维护凸壳的出入队判断条件：

一般先手画几个点，如果感觉画不出的话，再理性的去推。

比如掐头操作，可以假设后一个比前一个优，那么把需要满足的不等式暴力开出来。

就可以得到前两个的需满足的是什么。

又比如去尾操作，把一次函数先搞出来，根据求最大值还是最小值去具体分析：

最大值的话：

无论正负，应该满足最优解左侧的线段斜率大于当前斜率k，而右侧线段应小于当前斜率k。

即我们需要维护的是一个斜率单调递减的上凸壳，且一般只需维护小于当前斜率k的部分。

最小值反之。

看一下取最大值的两种情况：

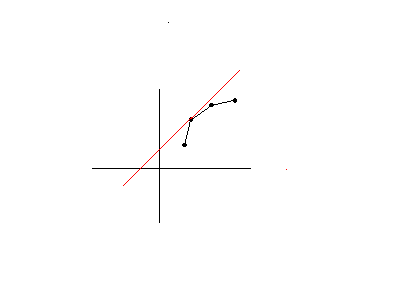
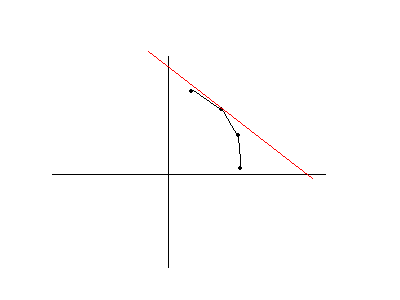
所以画图还是最好的。。。

查看全文

相关阅读:
poj 1328 Radar Installation (贪心)
hdu 2037 今年暑假不AC (贪心)
poj 2965 The Pilots Brothers' refrigerator (dfs)
poj 1753 Flip Game (dfs)
hdu 2838 Cow Sorting (树状数组)
hdu 1058 Humble Numbers (DP)
hdu 1069 Monkey and Banana (DP)
hdu 1087 Super Jumping! Jumping! Jumping! (DP)
必须知道的.NET FrameWork
使用记事本+CSC编译程序

原文地址：https://www.cnblogs.com/Bhllx/p/10360147.html