NOIP 2011 聪明的质检员-二分答案

先解释一下这个式子：

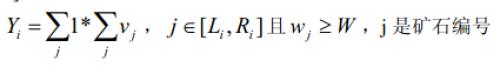
就是说如果区间[Li, Ri] 中 wj>=w的个数 乘以 所有的wj>=w的价值的和。

那么我们可以二分w的值，通过Y与S的值来调整w，

具体来讲，只要当下的Y大于S，那么增加Mid（增大Mid质量），否则减小Mid。

至于check，我们可以O（n）的预处理前缀和 and 前缀积。总复杂度 O（nlogn）。

代码可能有些傻，好像是Debug的时候一顿乱改搞的。。。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int gi () {
    int x=0, w=0; char ch=0;
    while (! (ch>='0' && ch<='9') ) {
        if (ch=='-') w=1;
        ch=getchar ();
    }
    while (ch>='0' && ch<='9') {
        x= (x<<3) + (x<<1) + (ch^48);
        ch=getchar ();
    }
    return w?-x:x;
}

const int Size=300010;
int n,m,l=2147483647,r,Mid,PreNum[Size];
ll S,PreJ[Size],Ans,Minx=999999999999999;
 
struct Stone {
    int wi, val;
}s[Size]; 

struct Area {
    int l, r;
}a[Size];

int main ()
{
    n=gi (), m=gi ();
    cin >> S;
    for (int i=1;i<=n;++i) {
        s[i].wi=gi (), s[i].val=gi ();
        l=min (l, s[i].wi);
        r=max (r, s[i].wi);
    }
    for (int i=1;i<=m;++i) {
        a[i].l=gi () ,a[i].r=gi ();
    }
    l--; r++;
    while (l<r) {
        Ans=0;
        Mid= (l+r) >> 1;
        for (int i=1;i<=n;++i) 
            if (s[i].wi>=Mid) {
                PreNum[i]=PreNum[i-1]+1;
                PreJ[i]=PreJ[i-1]+s[i].val;
            }
            else {
                PreNum[i]=PreNum[i-1];
                PreJ[i]=PreJ[i-1];    
            }
        for (int i=1;i<=m;++i) 
            Ans+= (PreNum[a[i].r]-PreNum[a[i].l-1]) * (PreJ[a[i].r]-PreJ[a[i].l-1]);
        if (Ans>S) l=Mid+1;
        else r=Mid;
        Minx=min (Minx, llabs (Ans-S) );
}
    printf ("%lld
", Minx);
    return 0;
}