python递归三战：Sierpinski Triangle、Tower of Hanoi、Maze Exploring

本文已做成视频教程投稿b站（视频版相对文本版有一些改进），点击观看视频教程

本文主要通过三个实例来帮助大家理解递归（其展示动画已上传B站）：

• 谢尔宾斯基三角形(Sierpinski Triangle),点击观看动画
• 汉诺塔(Tower of Hanoi),点击观看动画
• 迷宫探索(Maze Exploring),点击观看动画

本文代码已上传到github：https://github.com/BigShuang/recursion-with-turtle

本文参考文献：Problem Solving with Algorithms and Data Structures using Python

〇、递归算法三大原则

• 1、必须有一个基础情形(base case)
• 2、递归算法必须改变状态，来向1中的基础情形靠拢
• 3、递归算法必须递归地调用自己本身。

初次接触递归算法的人可能看不懂这三原则什么意思（很正常，我第一次就没看懂orz）。 
看不懂的话建议先看下面三个实战（看看里面是如何具体应用这三大原则解决问题的），看完之后再回过头来再看这三大原则，应该就很好理解了。

一、谢尔宾斯基三角形

谢尔宾斯基三角形是一种如下图所示的分形,点击观看动画

1，分析

其绘制过程如下

1. 绘制一个三角形（一般为等边三角形）
2. 取三角形的三边中点做顶点绘制一个小三角形，将上一级三角形分隔出三个小三角形。
3. 对分隔出的三个小三角形重复步骤2。

绘制过程可以无限重复下去，但是对于我们编写一个程序而言，必须要保证有穷性，所以需要在步骤三中对小三角形尺寸判断，当小三角形小到一定程度时退出循环。

有穷性：一个算法必须总是（对任何合法的输入值）在执行有穷步之后结束，且每一步都可在有穷时间内完成。

结合绘制过程，我们来使用递归三原则。分析一下递归部分应该要怎么写

# 核心递归函数，主要实现绘制过程中的第二第三步
def draw_nextone(triangle,basesize):
    """
    根据指定三角形三边中点绘制一个更小的三角形
    然后再取指定三角形被分割出来的三个小三角形为参数，递归调用自身
    :param triangle: 指定三角形三个顶点坐标，示例：((ax,ay),(bx,by),(cx,cy))。
    :param basesize: 绘制三角形的最小尺寸，当三角形尺寸小于该参数时退出递归，相当于递归三原则第一条中的基础情形(base case)
    """
    
    # 根据triangle可以得到三角形三顶点（A,B,C）坐标，以及边长l（三角形应该为等边三角形）
    # 如果边长l小于basesize，相当于到了递归算法的基础情形，退出递归,即
    # if l<basesize:
    #     return
    
    # 根据三角形三顶点(A,B,C)，算出三边中点(D,E,F)
    # 以三边中点(D,E,F)为顶点绘制出三角形（写一个专门的函数，用于根据三角形三顶点坐标绘制出三角形）
    # 此时指定的三角形ABC应该被新绘制的小三角形DEF分割成三个小三角形
    # 这三个小三角形应该分别为:ADF，DBE，FEC
    # 对这三个小三角形分别递归调用本函数draw_nextone，即
    # draw_nextone(ADF,basesize)
    # draw_nextone(DBE,basesize)
    # draw_nextone(FEC,basesize)

2，代码实现与回味

根据上一步的分析，绘制谢尔宾斯基三角形的最终代码

import turtle
import math


t=turtle.Turtle() # 初始化turtle对象
t.hideturtle() # 隐藏turtle画笔
t.speed(0) # 设置绘制速度。数值越小，绘制越快，0最快，10最慢


# =======
# 辅助用函数
# =======
def get_length(a,b):
    """返回a,b两点之间的距离"""
    ax,ay=a
    bx,by=b
    return math.sqrt((ax-bx)**2+(ay-by)**2)

def get_midpoint(a,b):
    """返回a,b两点的中点坐标"""
    ax, ay = a
    bx, by = b
    return (ax + bx) / 2, (ay + by) / 2

def draw_triangle(a,b,c):
    """以a,b,c为顶点绘制三角形"""
    ax,ay=a
    bx,by=b
    cx,cy=c

    t.penup()
    t.goto(ax,ay)
    t.pendown()
    t.goto(bx,by)
    t.goto(cx,cy)
    t.goto(ax,ay)
    t.penup()


# 核心递归函数，主要实现绘制过程中的第二第三步
def draw_nextone(triangle,basesize):
    """
    根据指定三角形三边中点绘制一个更小的三角形
    然后再取指定三角形被分割出来的三个小三角形为参数，递归调用自身
    :param triangle: 指定三角形三个顶点坐标，示例：((ax,ay),(bx,by),(cx,cy))。
    :param basesize: 绘制三角形的最小尺寸，当三角形尺寸小于该参数时退出递归，相当于递归三原则第一条中的基础情形(base case)
    :return: None
    """
    # 根据triangle可以得到三角形三顶点（A,B,C）坐标，以及边长l（三角形应该为等边三角形）
    a,b,c=triangle
    l=get_length(a,b)
    # 如果边长l小于basesize，相当于到了递归算法的基础情形，退出递归,即
    if l<basesize:
        return

    # 根据三角形三顶点(A,B,C)，算出三边中点(D,E,F)
    d=get_midpoint(a,b)
    e=get_midpoint(b,c)
    f=get_midpoint(c,a)
    # 以三边中点(D,E,F)为顶点绘制出三角形（写一个专门的函数，用于根据三角形三顶点坐标绘制出三角形）
    draw_triangle(d,e,f)
    # 此时指定的三角形ABC应该被新绘制的小三角形DEF分割成三个小三角形
    # 这三个小三角形应该分别为:ADF，DBE，FEC
    # 对这三个小三角形分别递归调用本函数draw_nextone，即
    draw_nextone([a,d,f],basesize)
    draw_nextone([d,b,e],basesize)
    draw_nextone([f,e,c],basesize)


# 绘制谢尔宾斯基三角形（原点为三角形中心，initsize为初始边长，basesize为其中允许的最小三角形边长）
def draw_Sierpinski_triangle(initsize,basesize):
    # 根据初始边长initsize算出三个顶点坐标
    sign3=math.sqrt(3) # 根号3
    ax,ay=0,initsize*sign3/3
    bx,by=initsize/2,-initsize*sign3/6
    cx,cy=-initsize/2,-initsize*sign3/6
    a=(ax,ay)
    b=(bx,by)
    c=(cx,cy)

    draw_triangle(a,b,c)
    draw_nextone([a,b,c],basesize)


    turtle.done() # 定住窗口，不然绘制完窗口会闪退


if __name__ == '__main__':
    initsize=400
    basesize=10
    draw_Sierpinski_triangle(initsize,basesize)　

　　

拓展阅读：http://interactivepython.org/runestone/static/pythonds/Recursion/pythondsSierpinskiTriangle.html

二、汉诺塔

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

抽象成数学问题：

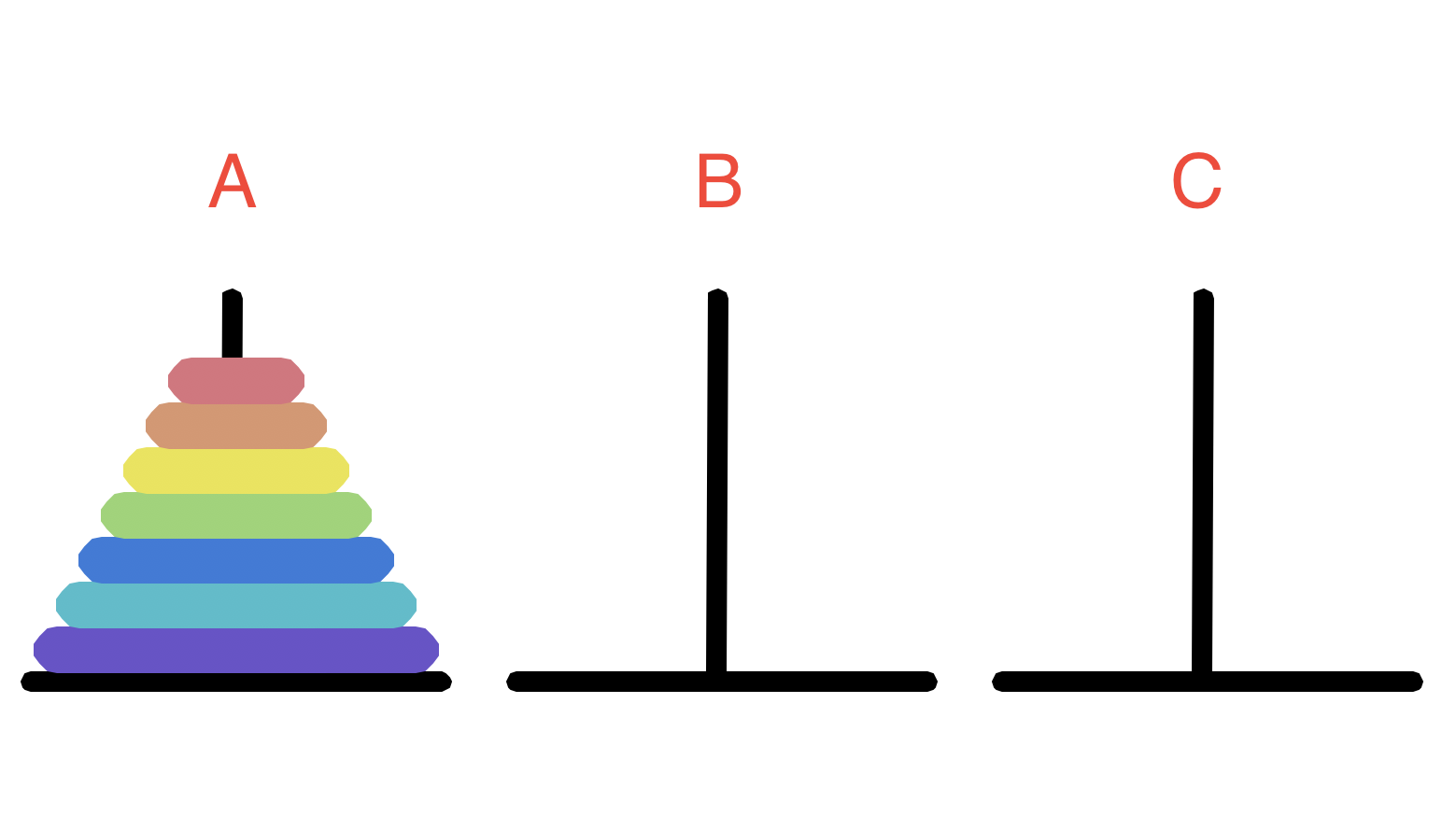
有三根相邻的柱子，标号为A,B,C，A柱子上从下到上按金字塔状叠放着n个大小不同（下面的大于上面）的圆盘，要把所有盘子一个一个移动到柱子C上，并且每次移动同一根柱子上都不能出现大盘子在小盘子上方，求移动过程。

点此观看移动动画

n=7时如下图：

 

1，思路分析

对于汉诺塔上的n个圆盘，我们从上到下（也是从小到大）分别用1，2，3、、、n去命名。

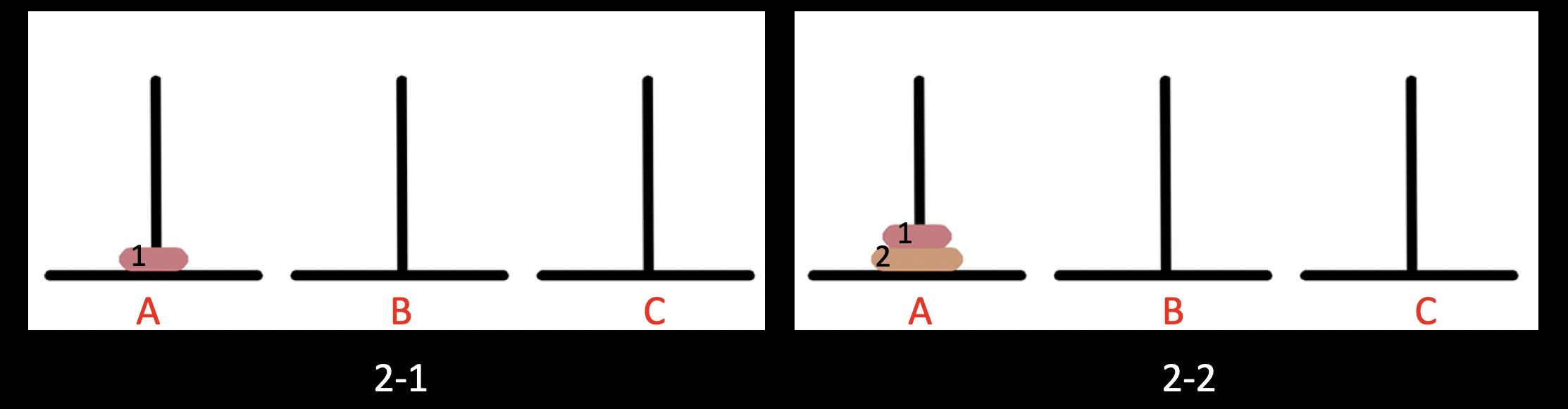
A为起点塔，C为目标塔，B为中转塔（中转塔的意义通过后文会明白）

• 当n=1时，如上图2-1所示

1 只需把圆盘1从起点塔A移到目标塔C即可。

• 当n=2时，如上图2-2所示

1 先将圆盘1从起点塔A移动到中转塔B

2 再将圆盘2从起点塔A移动到目标塔C

3 最后将圆盘1从中转塔B（中转塔）移动到目标塔C

• 当n=3时

1 先将圆盘12看作一个整体从起点塔A移动到中转塔B（具体移动方法可看n=2，上面已经记录了n=2时的移动方法，只不过在本次移动过程中，B是本次移动的目标塔，C则是本次移动的中转塔）

2 再将圆盘3从起点塔A移动到目标塔C

3 最后将圆盘12看作一个整体从中转塔B移动到目标塔C（可参考本情况的步骤一）

那么顺着这个逻辑往下走，我们不难猜想到

• 当n=k时(k>1)

1 先将圆盘1到k-1看作一个整体从起点塔A移动到中转塔B

2 再将圆盘k从起点塔A移动到目标塔C

3 最后将圆盘1到k-1看作一个整体从中转塔B移动到目标塔C

 上面的这个过程可以算是分治算法（而这个算法往往通过递归的方式去实现）

2，分治法

分治法，简单的来讲，就是分而治之（英文：Divide and Conquer）；其核心思想，就是把一个复杂的大问题，拆分成一些规模较小的子问题（与原问题相同或相似），并可以对这些子问题反复地（递归地）执行这个过程，直至问题规模减小到可以求解（这种情况对应递归算法三原则中的基础情况）。

具体到汉诺塔，那么复杂的大问题就是对于n层的汉诺塔，我们该怎么去从起始塔A移动到终止塔C,这个问题难以直接解决，

那么我们首先把这个问题拆分成三个规模较小的问题：

• 1 先将圆盘1到n-1看作一个整体从起点塔A移动到中转塔B（用塔C作为本步骤的中转）
• 2 再将圆盘n从起点塔A移动到目标塔C
• 3 最后将圆盘1到n-1看作一个整体从中转塔B移动到目标塔C（用塔A作为本步骤的中转）

其中2可以直接解决，1和3仍然难以直接解决，那么我们可以将1继续拆分成是那个规模更小的问题（3类似）：

• 1-1 先将圆盘1到n-2看作一个整体从A移动到C（用塔B作为本步骤的中转）
• 1-2 再将圆盘n-1从起点塔A移动到B
• 1-3 最后将圆盘1到n-2看作一个整体从C移动到A（用塔A作为本步骤的中转）

其中1-2可以直接解决，对于1-1和1-3我们可以继续拆分，直至只剩一个圆盘的情况，此时即可直接解决。

上过高中的小伙伴应该都学过数学归纳法，其实上面的这些也可以用数学归纳法去做一个严谨的证明。

3，数学归纳法

这一步是为了给上面的分析提供一个严谨的证明，对思路有一定启发，但是不看问题也不大，不太感兴趣的话可以直接跳过～

数学归纳法的基本步骤分两步：

1. 证明当n= 1时命题成立。
2. 假设n=m时命题成立，那么可以推导出在n=m+1时命题也成立。（m代表任意自然数）

对于本问题，n层汉诺塔

• 当n=1时，只需把圆盘1从起点塔A移到目标塔C即可。
• 假设n=m时，圆盘1-m可以通过上文讨论的方法从起点塔A移到目标塔C，那么圆盘1-m也可以从A移动到B，然后圆盘m+1可以移动到C，最后圆盘1-m可以从B移动到C。

所以上文讨论的方法对于所有正整数n都是有效的。

4，代码实现

代码如下

# 移动指定层圆盘diskIndex，从fromPole出发，到达toPole
def moveDisk(diskIndex,fromPole,toPole):
    """
    :param diskIndex: 圆盘的索引（从上往下，第一层为1，第二层为2、、、第n层为n）
    :param fromPole: 出发的柱子（起点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    print_str='Move disk %s form %s to %s'%(diskIndex,fromPole,toPole)
    print(print_str)


# 核心函数，入口
def moveTower(height,fromPole, withPole, toPole):
    """
    :param height: 汉诺塔高度——层数
    :param fromPole: 出发的柱子（起点）
    :param withPole: 进过的柱子（中转点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    if height == 1:
        # 基础情形：一层的汉诺塔
        moveDisk(1,fromPole, toPole)
        return

    # 先将圆盘1到n - 1看作一个整体从起点塔移动到中转塔（用目标塔作为本步骤的中转）
    moveTower(height-1,fromPole,toPole,withPole)
    # 再将圆盘n从起点塔A移动到目标塔C
    moveDisk(height,fromPole,toPole)
    # 最后将圆盘1到n - 1看作一个整体从中转塔移动到目标塔（用起点塔作为本步骤的中转）
    moveTower(height-1,withPole,fromPole,toPole)


if __name__ == '__main__':
    # 调用
    # 三层汉诺塔，A为出发柱子，B为中转柱子，C为目标柱子
    moveTower(3,"A","B","C")

   本代码输入如下（此时为三层汉诺塔）

Move disk 1 form A to C
Move disk 2 form A to B
Move disk 1 form C to B
Move disk 3 form A to C
Move disk 1 form B to A
Move disk 2 form B to C
Move disk 1 form A to C

5，可视化汉诺塔代码实现（使用turtle）

代码如下

import turtle

# ==============
#  常量设置
# ==============
N=3 # 汉诺塔层数限制

BasePL=12   # plate的大小基数，修改这个能够调整plate的大小
TowerP=5    # Tower的线宽
TowerW=110  # Tower的底座宽度
TowerH=200  # Tower的高度
TowerSpace=260  # Tower的之间的距离，从中心到中心
HORIZON=-100    # Tower的底座高度，用于定位
# 动画速度，5是比较适中的速度
PMS=5

# 优化处理
Isjump=True

POLES={
    "1": [],
    "2": [],
    "3": [],
}
PLATES=[] # 存储所有圆盘对象

# 塔的颜色
LineColor="black"
# 多个盘子的颜色
FillColors=[
    "#d25b6a",
    "#d2835b",
    "#e5e234",
    "#83d05d",
    "#2862d2",
    "#35b1c0",
    "#5835c0"
]
# 建立窗体
SCR=turtle.Screen()
# SCR.tracer()
SCR.setup(800,600) #设置窗体大小


# 设置圆盘形状
def set_plate(pi=0):
    _pi=pi+2
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)
    t.penup()
    t.begin_poly()
    t.left(90)
    t.forward(BasePL*_pi)
    t.circle(BasePL, 180)
    t.forward(BasePL * 2 * _pi)
    t.circle(BasePL, 180)
    t.forward(BasePL * _pi)
    t.end_poly()
    p = t.get_poly()
    pname='plate_%s'%pi
    SCR.register_shape(pname, p)


# 设置塔柱形状
def set_tower():
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)
    t.penup()

    t.begin_poly()
    t.left(90)
    t.forward(TowerW)
    t.circle(-TowerP, 180)
    t.forward(TowerW)
    t.forward(TowerW)
    t.circle(-TowerP, 180)
    t.forward(TowerW-TowerP/2)

    t.left(90)
    t.forward(TowerH)
    t.circle(-TowerP, 180)
    t.forward(TowerH)
    t.end_poly()
    p = t.get_poly()
    SCR.register_shape('tower', p)


# 绘制塔柱
def draw_towers():
    set_tower()
    for tx in [-TowerSpace,0,TowerSpace]:
        t3 = turtle.Turtle('tower')
        t3.penup()
        t3.goto(tx,HORIZON)


# 绘制圆盘
def draw_plates(pn=4):
    plates=[]
    for i in range(pn):
        set_plate(i)
        _plate='plate_%s'%i
        _p=turtle.Turtle(_plate)
        _colorIdx = i % len(FillColors)
        _color=FillColors[_colorIdx]

        _p.color(_color,_color)
        _p.speed(PMS)
        plates.append(_p)
    # 反序，大的在前，小的在后
    global PLATES
    PLATES = plates[:]

# 绘制移动过程
def draw_move(diskIndex, fromPindex, toPindex):
    p=PLATES[diskIndex-1]
    index_loc={
        "A":1,
        "B":2,
        "C":3
    }
    toP=index_loc.get(toPindex,None)
    fromP=index_loc.get(fromPindex,None)

    p.penup()

    mx = (toP - 2) * TowerSpace
    my = HORIZON + len(POLES[str(toP)]) * BasePL * 2

    if fromP!=None:
        POLES[str(fromP)].remove(p)
        if Isjump:
            px,py=p.pos()
            p.goto(px,TowerH+py)
            p.goto(mx,TowerH+py)

    p.goto(mx, my)
    POLES[str(toP)].append(p)


# 将所有圆盘移动到起点
def movetoA(n,fromPindex):
    for i in range(n,0,-1):
        draw_move(i,None,fromPindex)


# 移动指定层圆盘diskIndex，从fromPole出发，到达toPole
def moveDisk(diskIndex,fromPole,toPole):
    """
    :param diskIndex: 圆盘的索引（从上往下，第一层为1，第二层为2、、、第n层为n）
    :param fromPole: 出发的柱子（起点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    draw_move(diskIndex, fromPole, toPole)


# 核心函数，入口
def moveTower(height,fromPole, withPole, toPole):
    """
    :param height: 汉诺塔高度——层数
    :param fromPole: 出发的柱子（起点）
    :param withPole: 进过的柱子（中转点）
    :param toPole: 要到达的柱子（终点）
    :return:
    """
    if height == 1:
        # 基础情形：一层的汉诺塔
        moveDisk(1,fromPole, toPole)
        return

    # 先将圆盘1到n - 1看作一个整体从起点塔移动到中转塔（用目标塔作为本步骤的中转）
    moveTower(height-1,fromPole,toPole,withPole)
    # 再将圆盘n从起点塔A移动到目标塔C
    moveDisk(height,fromPole,toPole)
    # 最后将圆盘1到n - 1看作一个整体从中转塔移动到目标塔（用起点塔作为本步骤的中转）
    moveTower(height-1,withPole,fromPole,toPole)


if __name__ == '__main__':
    # 调用
    # 三层汉诺塔，A为出发柱子，B为中转柱子，C为目标柱子
    n=3
    
    SCR.tracer(0)
    draw_towers()
    draw_plates(n)
    movetoA(n,"A")
    SCR.tracer(1)

    SCR.delay(1)

    moveTower(n,"A","B","C")
    turtle.done()

三、迷宫探索

点此观看动画

迷宫如下图所示：

 

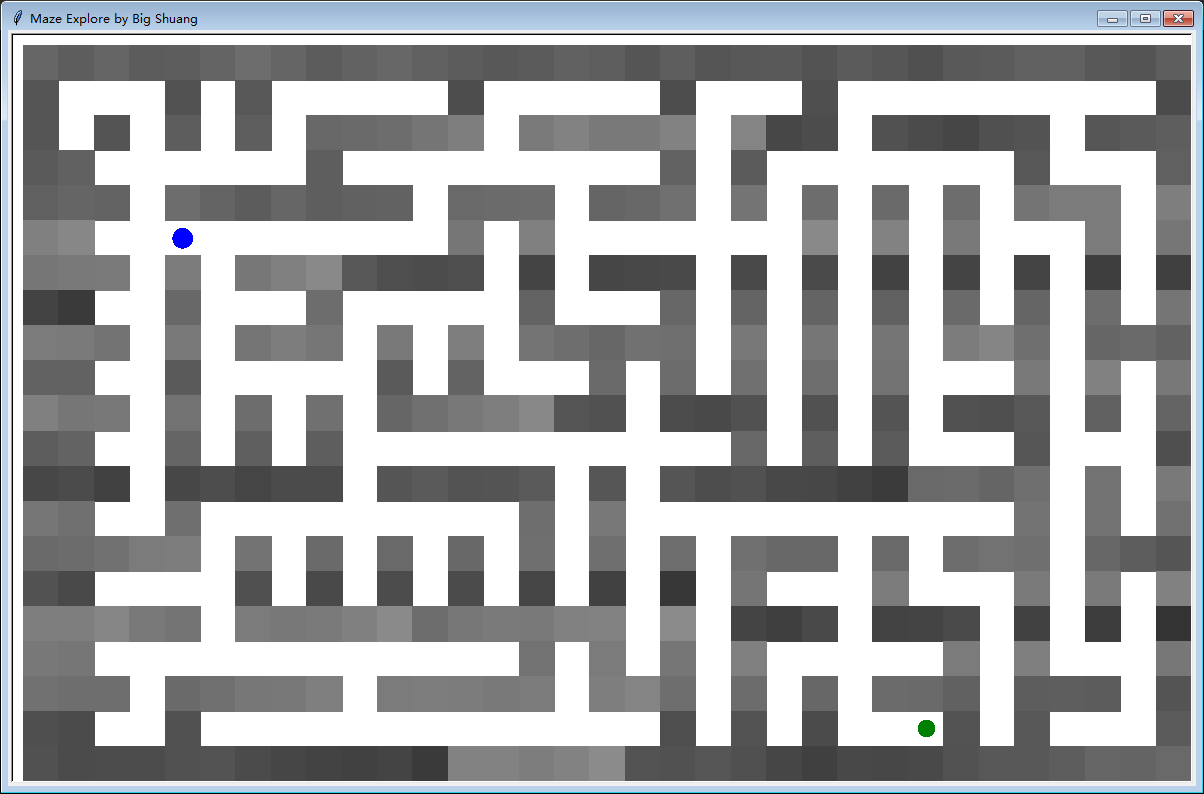
迷宫文本301.txt如下

迷宫文本需要在代码所在文件夹里面，新建一个text文件夹,放在text文件夹里面

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 0 0 0 2 0 2 0 0 0 0 0 2 0 0 0 0 0 2 0 0 0 2 0 0 0 0 0 0 0 0 0 1
1 0 1 0 1 0 1 0 1 2 1 2 1 0 1 2 1 2 1 0 1 2 1 0 1 2 1 2 1 0 1 2 1
1 1 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 2 0 2 0 0 0 0 0 0 0 2 0 0 0 1
1 1 1 0 1 2 1 2 1 2 1 0 1 2 1 0 1 2 1 0 1 0 1 0 1 0 1 0 1 2 1 0 1
1 1 0 0 S 0 0 0 0 0 0 0 2 0 2 0 0 0 0 0 0 0 2 0 2 0 2 0 0 0 2 0 1
1 1 1 0 1 0 1 2 1 2 1 2 1 0 1 0 1 2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
1 1 0 0 2 0 0 0 2 0 0 0 0 0 2 0 0 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0 1
1 1 1 0 1 0 1 2 1 0 1 0 1 0 1 2 1 2 1 0 1 0 1 0 1 0 1 2 1 0 1 2 1
1 1 0 0 2 0 0 0 0 0 2 0 2 0 0 0 2 0 2 0 2 0 2 0 2 0 0 0 2 0 2 0 1
1 1 1 0 1 0 1 0 1 0 1 2 1 2 1 2 1 0 1 2 1 0 1 0 1 0 1 2 1 0 1 0 1
1 1 0 0 2 0 2 0 2 0 0 0 0 0 0 0 0 0 0 0 2 0 2 0 2 0 0 0 2 0 0 0 1
1 1 1 0 1 2 1 2 1 0 1 2 1 2 1 0 1 0 1 2 1 2 1 2 1 2 1 2 1 0 1 0 1
1 1 0 0 2 0 0 0 0 0 0 0 0 0 2 0 2 0 0 0 0 0 0 0 0 0 0 0 2 0 2 0 1
1 1 1 2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 2 1 0 1 0 1 2 1 0 1 2 1
1 1 0 0 0 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0 0 0 2 0 0 0 2 0 2 0 1
1 1 1 2 1 0 1 2 1 2 1 2 1 2 1 2 1 0 1 0 1 2 1 0 1 2 1 0 1 0 1 0 1
1 1 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 0 2 0 2 0 0 0 0 0 2 0 2 0 0 0 1
1 1 1 0 1 2 1 2 1 0 1 2 1 2 1 0 1 2 1 0 1 0 1 0 1 2 1 0 1 2 1 0 1
1 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 0 2 0 0 E 2 0 2 0 0 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

其中1和2都是墙，0是路，S为起点，E为终点。

1，实现迷宫可视化（使用turtle）

编写函数用于读取迷宫，存到一个二维的列表里面。代码如下

# 从txt文本中将迷宫提取出来
def get_maze_info(filename):
    with open(filename,'r') as f:
        fl = f.readlines()

    maze_list =[]
    for line in fl:
        line = line.strip()
        line_list = line.split(" ")
        maze_list.append(line_list)

    return maze_list　

编写具体绘制的方法

# 读取迷宫文本信息
txt_path = "text/301.txt"
mazeList = get_maze_info(txt_path)

# 获取迷宫的长宽，R-行数，C-列数
R, C = len(mazeList), len(mazeList[0])
# 设置用于绘制迷宫的单元格的尺寸
cellsize = 20


import turtle  # 导入turtle库
scr = turtle.Screen()  # 建立屏幕对象 src
scr.setup(width=C*cellsize,height=R*cellsize)  # 设置屏幕尺寸大小（刚好能够显示所有迷宫的单元格）

t = turtle.Turtle()  # 建立画笔对象 t
t.speed(0)  # 设置画笔对象的速度，0是最快的，1-10依次变快


# 根据迷宫信息绘制迷宫
def draw_maze(mazeList):
    scr.tracer(0)  # 具体我也没搞明白，只知道能够跳过漫长的绘制动画

    #　rowIndex，行号，相当于ｙ
    for rowIndex in range(len(mazeList)):
        row = mazeList[rowIndex]
        for columnIndex in range(len(row)):
            # columnIndex，列号，相当于ｘ
            item = row[columnIndex]
            if item == "1" or item == "2":
                draw_cell(columnIndex,rowIndex)  # 绘制具体的单元格


def draw_cell(ci,ri):
    """
    绘制一个墙体单元格,
    :param ci: 单元格所在列序号
    :param ri: 单元格所在行序号
    :return:
    """
    # 计算出单元格左上角的坐标，计算演示图在本段代码下方
    tx = ci*cellsize - C*cellsize/2
    ty = R*cellsize/2 - ri*cellsize
    t.penup()  # 提起画笔
    t.goto(tx,ty)  # 根据计算出来的坐标移动到单元格左上角
    t.pendown()  # 放下画笔
    t.begin_fill()  # 开启填充，此时经过的形状会被填充
    # 绘制一个边长为cellsize的正方形
    for i in range(4):
        t.fd(cellsize)
        t.right(90)
    t.end_fill() # 关闭填充

计算单元格坐标演示图

 调用上面写好的方法就可以绘制出迷宫了

draw_maze(mazeList)
# 绘制玩的话会发现窗口会自动退出掉，加入下面一行代码就可以维持住窗口
turtle.done()

此时绘制出来会如下图

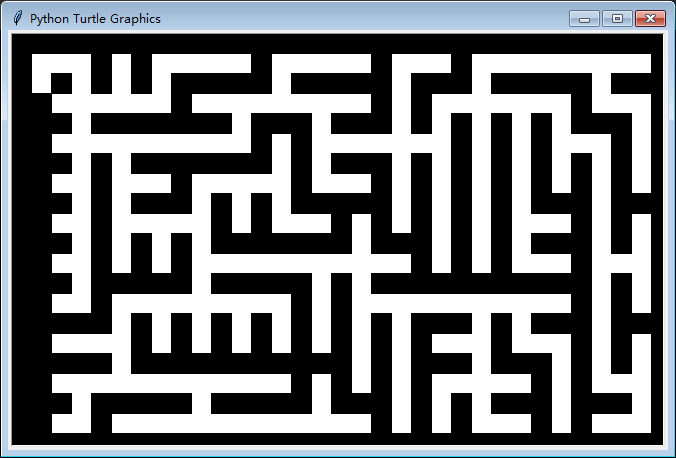
 我们这样全黑的迷宫样式上并不美观，可以设置不同的灰度值让黑色有变化，从而更加耐看

做法也很简单，只需要简单修改下draw_cell 方法就好（在开头和中间部分各加上两行代码，如下）

import random  # 导入随机数模块
scr.colormode(255)  # 设置颜色模式


def draw_cell(ci,ri):
    """
    绘制一个墙体单元格,
    :param ci: 单元格所在列序号
    :param ri: 单元格所在行序号
    :return:
    """
    # 计算出单元格左上角的坐标，计算演示图在本段代码下方
    tx = ci*cellsize - C*cellsize/2
    ty = R*cellsize/2 - ri*cellsize
    t.penup()  # 提起画笔
    t.goto(tx,ty)  # 根据计算出来的坐标移动到单元格左上角

    # 为了美化样式，我们需要把黑色弄的有变化些，即有不同的灰度
    v = random.randint(100,150)
    t.color(v,v,v)

    t.pendown()  # 放下画笔
    t.begin_fill()  # 开启填充，此时经过的形状会被填充
    # 绘制一个边长为cellsize的正方形
    for i in range(4):
        t.fd(cellsize)
        t.right(90)
    t.end_fill() # 关闭填充

此时绘制出来的迷宫如下图

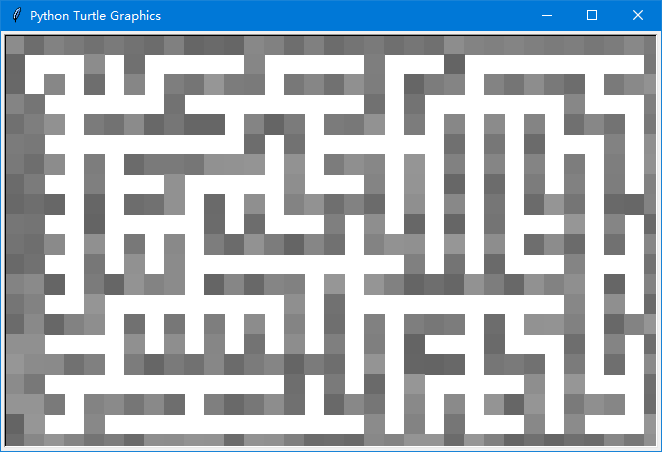
 然后迷宫需要再把起点和终点绘制出来。

写一个专门的方法draw_dot去绘制点（可以设置颜色）

# 新建一个画笔对象用于绘制点
dot_t = turtle.Turtle()
# 设置打点的尺寸
dot_size = 15


def draw_dot(ci,ri,color = "black"):
    """
        在制定单元格绘制圆点,
        :param ci: 单元格所在列序号
        :param ri: 单元格所在行序号
        :param color: 圆点的颜色
        :return:
    """
    # 计算出单元格左上角的坐标，计算演示图在本段代码下方
    tx = ci * cellsize - C * cellsize / 2
    ty = R * cellsize / 2 - ri * cellsize
    # 进一步计算出所在单元格中心的坐标
    cx = tx + cellsize / 2
    cy = ty - cellsize / 2
    dot_t.penup()

    dot_t.goto(cx,cy)
    dot_t.dot(dot_size,color)

 然后再在函数draw_maze里面加入对起点和终点的判断与绘制（其实就是在最后面加上四行代码），改动后的方法代码如下

# 根据迷宫信息绘制迷宫
def draw_maze(mazeList):
    scr.tracer(0)  # 具体我也没搞明白，只知道能够跳过漫长的绘制动画

    # 　rowIndex，行号，相当于ｙ
    for rowIndex in range(len(mazeList)):
        row = mazeList[rowIndex]
        for columnIndex in range(len(row)):
            # columnIndex，列号，相当于ｘ
            item = row[columnIndex]
            if item == "1" or item == "2":
                draw_cell(columnIndex, rowIndex)  # 绘制具体的单元格
            elif item == "S":
                # 设置起点颜色为蓝色
                draw_dot(columnIndex, rowIndex,"blue")
            elif item == "E":
                # 设置终点颜色为绿色
                draw_dot(columnIndex, rowIndex, "green")

此时绘制出来的迷宫如下图

 

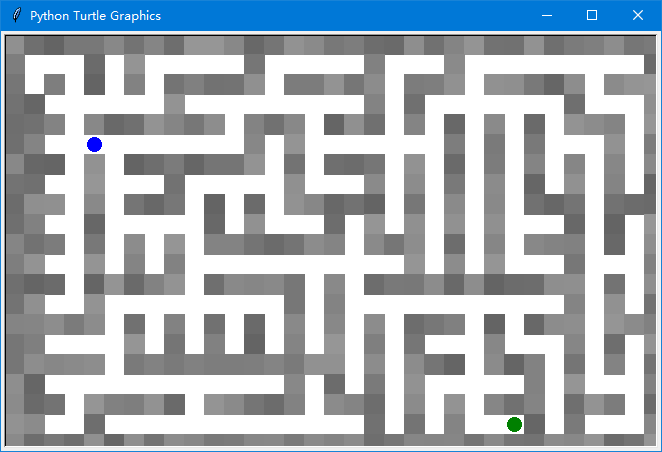
2，寻路思路分析

使用上面递归三原则原理来分析以下

其探索过程为：

从起点出发，分别按顺序往上下左右四个方向去探索（即移动到上下左右的相邻单元格），

在这一过程中递归地讲对探索后的相邻单元格进行进一步四周的探索（即将该相邻单元格当做新的起点去执行上一步骤，直至探索完成或失败，才开始下一个方向的探索）

探索的具体过程可以分下面几种情况：

1. 找到终点，探索完成，然后告诉上一步这一步探索成功
2. 找到墙或者探索过的点（或者超出迷宫的点），探索失败，然后还是告诉上一步这一步探索是失败的
3. 向某个方向的探索得出的结论是成功的（源于1），那么探索完成，不在探索，并且告诉上一步探索这一方向是能够探索成功的
4. 向某个方向的探索得出的结论是失败的（源于2），那么换一个方向进行探索
5. 向所有方向探索都失败了，那么探索失败，并告诉上一步这一方向探索是失败的

代码如下

# 新建一个画笔对象用于绘制探索过程（也就是路径）
line_t = turtle.Turtle()
line_t.pensize(5)
line_t.speed(0)

def start_search(mazeList):
    # 获取起点所在行和列的序号
    start_c, start_r = 0, 0
    # 　rowIndex，行号，相当于ｙ
    for rowIndex in range(len(mazeList)):
        row = mazeList[rowIndex]
        for columnIndex in range(len(row)):
            # columnIndex，列号，相当于ｘ
            item = row[columnIndex]
            if item == "S":
                start_c, start_r = columnIndex, rowIndex

    line_t.penup()
    draw_path(start_c, start_r)
    line_t.pendown()
    # 进入递归搜索
    searchNext(mazeList, start_c, start_r)


# 核心递归探索方法，从该点出发，递归地去探索四个方向
def searchNext(mazeList, ci, ri):
    # 1,找到终点，探索完成，然后告诉上一步这一步探索成功
    if mazeList[ri][ci] == "E":
        draw_path(ci, ri)
        return True

    # 2,找到墙或者探索过的点（或者超出迷宫的点），探索失败，然后还是告诉上一步这一步探索是失败的
    if not (0 <= ci < len(mazeList[0]) and 0 <= ri < len(mazeList)):
        return False
    if mazeList[ri][ci] in ["1", "2","TRIED"]:
        return False

    # 探索后标记该点为已探索过
    mazeList[ri][ci] = "TRIED"
    draw_path(ci, ri)

    # 上下左右四个探索的方向
    direction = [
        [1, 0],
        [-1, 0],
        [0, 1],
        [0, -1],
    ]

    for d in direction:
        dc, dr =d

        found = searchNext(mazeList, ci + dc, ri + dr)
        if found:
            # 3,向某个方向的探索得出的结论是成功的（源于1），那么探索完成，不在探索，并且告诉上一步探索这一方向是能够探索成功的
            draw_path(ci, ri, "green")
            return True
        else:
            # 4,向某个方向的探索得出的结论是失败的（源于2），那么换一个方向进行探索
            draw_path(ci, ri, "red")

    # 5,向所有方向探索都失败了，那么探索失败，并告诉上一步这一方向探索是失败的
    return False


def draw_path(ci,ri,color = "blue"):
    # 计算出单元格左上角的坐标，计算演示图在本段代码下方
    tx = ci * cellsize - C * cellsize / 2
    ty = R * cellsize / 2 - ri * cellsize
    # 进一步计算出所在单元格中心的坐标
    cx = tx + cellsize / 2
    cy = ty - cellsize / 2

    line_t.color(color)
    line_t.goto(cx, cy)

最后调用该方法，效果就和我在b站的投稿差不多了

draw_maze(mazeList)
scr.tracer(1)
start_search(mazeList)
# 绘制玩的话会发现窗口会自动退出掉，加入下面一行代码就可以维持住窗口
turtle.done()

寻路完如下图所示

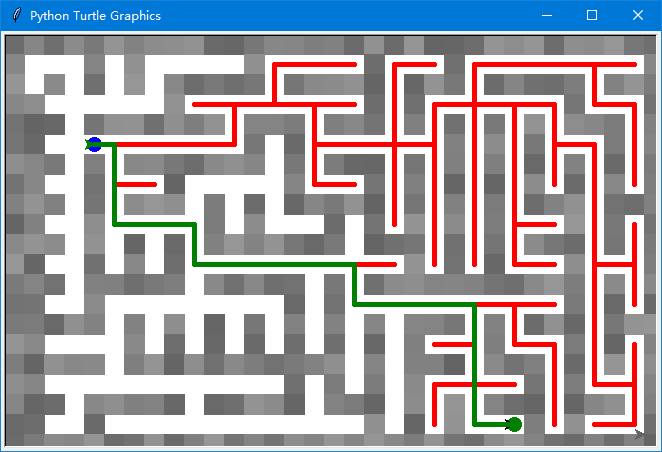
3，最终代码

 梳理代码后如下

import turtle
import random


# ========================
# 常量
# ========================
# 设置用于绘制迷宫的单元格的尺寸
CELL_SIZE = 20
# 设置打点(起点和终点)的尺寸
DOT_SIZE = 15
# 设置探索过程（也就是路径）的尺寸
LINE_SIZE = 5
TXT_PATH = "text/301.txt"


# ========================
# 初始化一些turtle画笔对象
# ========================
scr = turtle.Screen()  # 建立屏幕对象 src
scr.colormode(255)  # 设置颜色模式为rgb数值模式

wall_t = turtle.Turtle()  # 建立画笔对象 wall_t 用于绘制墙体
dot_t = turtle.Turtle()  # 建立画笔对象 dot_t 用于绘制点
line_t = turtle.Turtle() # 建立画笔对象 line_t 用于绘制探索过程（也就是路径）
line_t.pensize(LINE_SIZE)


# 从txt文本中将迷宫提取出来
def get_maze_info(filename):
    with open(filename, 'r') as f:
        fl = f.readlines()

    maze_list = []
    for line in fl:
        line = line.strip()
        line_list = line.split(" ")
        maze_list.append(line_list)

    return maze_list


mazeList = get_maze_info(TXT_PATH)
# 获取迷宫的长宽，R-行数，C-列数
R, C = len(mazeList), len(mazeList[0])
scr.setup(width=C * CELL_SIZE, height=R * CELL_SIZE)  # 设置屏幕尺寸大小（刚好能够显示所有迷宫的单元格）


def draw_cell(ci, ri):
    """
    绘制一个墙体单元格,
    :param ci: 单元格所在列序号
    :param ri: 单元格所在行序号
    :return:
    """
    # 计算出单元格左上角的坐标，计算演示图在本段代码下方
    tx = ci * CELL_SIZE - C * CELL_SIZE / 2
    ty = R * CELL_SIZE / 2 - ri * CELL_SIZE
    wall_t.penup()  # 提起画笔
    wall_t.goto(tx, ty)  # 根据计算出来的坐标移动到单元格左上角

    # 为了美化样式，我们需要把黑色弄的有变化些，即有不同的灰度
    v = random.randint(100, 150)
    wall_t.color(v, v, v)

    wall_t.pendown()  # 放下画笔
    wall_t.begin_fill()  # 开启填充，此时经过的形状会被填充
    # 绘制一个边长为CELL_SIZE的正方形
    for i in range(4):
        wall_t.fd(CELL_SIZE)
        wall_t.right(90)
    wall_t.end_fill()  # 关闭填充
    

def draw_dot(ci, ri, color="black"):
    """
        在制定单元格绘制圆点,
        :param ci: 单元格所在列序号
        :param ri: 单元格所在行序号
        :param color: 圆点的颜色
        :return:
    """
    # 计算出单元格左上角的坐标，计算演示图在本段代码下方
    tx = ci * CELL_SIZE - C * CELL_SIZE / 2
    ty = R * CELL_SIZE / 2 - ri * CELL_SIZE
    # 进一步计算出所在单元格中心的坐标
    cx = tx + CELL_SIZE / 2
    cy = ty - CELL_SIZE / 2
    dot_t.penup()

    dot_t.goto(cx, cy)
    dot_t.dot(DOT_SIZE, color)


# 根据迷宫信息绘制迷宫
def draw_maze(mazeList):
    scr.tracer(0)  # 具体我也没搞明白，只知道能够跳过漫长的绘制动画

    # 　rowIndex，行号，相当于ｙ
    for rowIndex in range(len(mazeList)):
        row = mazeList[rowIndex]
        for columnIndex in range(len(row)):
            # columnIndex，列号，相当于ｘ
            item = row[columnIndex]
            if item == "1" or item == "2":
                draw_cell(columnIndex, rowIndex)  # 绘制具体的单元格
            elif item == "S":
                # 设置起点颜色为蓝色
                draw_dot(columnIndex, rowIndex, "blue")
            elif item == "E":
                # 设置终点颜色为绿色
                draw_dot(columnIndex, rowIndex, "green")


# 绘制路径，以画笔当前所在位置为起点，以单元格（ci, ri）中心作为终点，绘制路径。
def draw_path(ci, ri, color="blue"):
    # 计算出单元格左上角的坐标，计算演示图在本段代码下方
    tx = ci * CELL_SIZE - C * CELL_SIZE / 2
    ty = R * CELL_SIZE / 2 - ri * CELL_SIZE
    # 进一步计算出所在单元格中心的坐标
    cx = tx + CELL_SIZE / 2
    cy = ty - CELL_SIZE / 2

    line_t.color(color)
    line_t.goto(cx, cy)


# 核心递归探索方法，从该点出发，递归地去探索四个方向
def searchNext(mazeList, ci, ri):
    # 1,找到终点，探索完成，然后告诉上一步这一步探索成功
    if mazeList[ri][ci] == "E":
        draw_path(ci, ri)
        return True

    # 2,找到墙或者探索过的点（或者超出迷宫的点），探索失败，然后还是告诉上一步这一步探索是失败的
    if not (0 <= ci < len(mazeList[0]) and 0 <= ri < len(mazeList)):
        return False
    if mazeList[ri][ci] in ["1", "2", "TRIED"]:
        return False

    # 探索后标记该点为已探索过
    mazeList[ri][ci] = "TRIED"
    draw_path(ci, ri)

    # 上下左右四个探索的方向
    direction = [
        [1, 0],
        [-1, 0],
        [0, 1],
        [0, -1],
    ]

    for d in direction:
        dc, dr = d

        found = searchNext(mazeList, ci + dc, ri + dr)
        if found:
            # 3,向某个方向的探索得出的结论是成功的（源于1），那么探索完成，不在探索，并且告诉上一步探索这一方向是能够探索成功的
            draw_path(ci, ri, "green")
            return True
        else:
            # 4,向某个方向的探索得出的结论是失败的（源于2），那么换一个方向进行探索
            draw_path(ci, ri, "red")

    # 5,向所有方向探索都失败了，那么探索失败，并告诉上一步这一方向探索是失败的
    return False


#　开始迷宫探索
def start_search(mazeList):
    # 获取起点所在行和列的序号
    start_c, start_r = 0, 0
    # 　rowIndex，行号，相当于ｙ
    for rowIndex in range(len(mazeList)):
        row = mazeList[rowIndex]
        for columnIndex in range(len(row)):
            # columnIndex，列号，相当于ｘ
            item = row[columnIndex]
            if item == "S":
                start_c, start_r = columnIndex, rowIndex

    line_t.penup()
    draw_path(start_c, start_r)
    line_t.pendown()
    # 进入递归搜索
    searchNext(mazeList, start_c, start_r)
    
    
draw_maze(mazeList)
scr.tracer(1)
start_search(mazeList)
# 绘制玩的话会发现窗口会自动退出掉，加入下面一行代码就可以维持住窗口
turtle.done()