大爽Python入门练习题 44 生成螺旋矩阵（二维列表）

大爽Python入门练习题总目录

第四章 中期练习题 冷酷&凶残 第4题

题目

出处: leetcode-54: Spiral Matrix
原题是输出，这里是生成，其实核心逻辑是相通的。

简介

实现一个函数get_spiral_matrix(m, n):，
接受两个正整数m和n作为参数（m和n一定都大于0），
返回m行n列的矩阵（二维列表），
矩阵的值为1到\(m \times n\)
按螺旋顺序插入得到（详细解释见下方）。

详细说明

螺旋顺序如下图所示

这是一个3行4列的效果

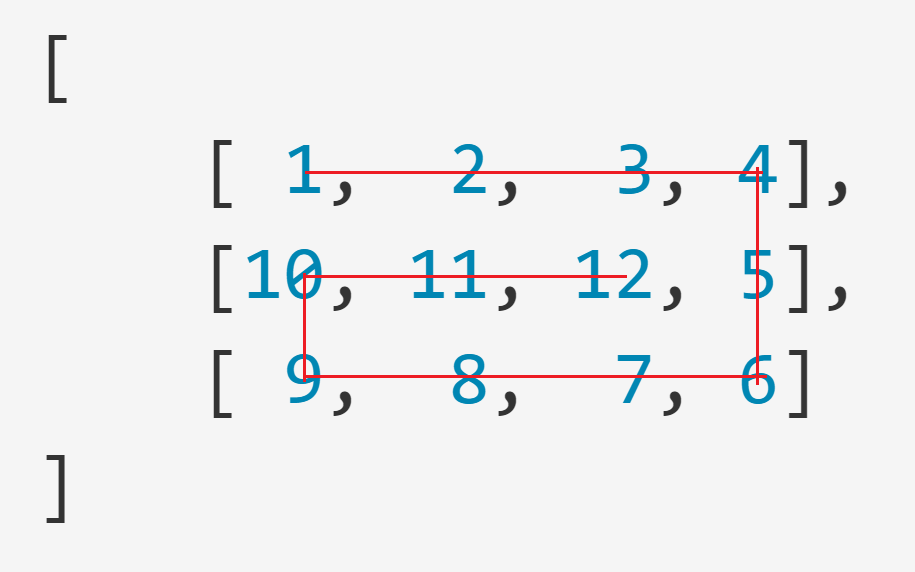
这是一个6行5列的效果

示例

get_spiral_matrix(3, 4)的返回值为
(下面手动为列表换行方便观察)

[
    [1, 2, 3, 4],
    [10, 11, 12, 5],
    [9, 8, 7, 6]
]

get_spiral_matrix(6, 5)的返回值为
(下面手动为列表换行方便观察)

[
    [1, 2, 3, 4, 5],
    [18, 19, 20, 21, 6],
    [17, 28, 29, 22, 7],
    [16, 27, 30, 23, 8],
    [15, 26, 25, 24, 9],
    [14, 13, 12, 11, 10]
]

分割线

本小段没有实际意义，
仅用于分隔题目和答案。
防止学生无意中直接看到答案，
影响思路。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。
。

答案

参考答案1

def get_spiral_matrix(m, n):
    matrix = [
        [0 for ci in range(n)] for ri in range(m)
    ]
    min_v = m
    if n < m:
        min_v = n

    layer = (min_v + 1) // 2
    count = 0
    for li in range(layer):
        for ci in range(li, n-li):
            count += 1
            matrix[li][ci] = count

        for ri in range(li + 1, m-li-1):
            count += 1
            matrix[ri][n-li-1] = count

        if li < m-li-1:
            for ci in range(n-li-1, li-1, -1):
                count += 1
                matrix[m-li-1][ci] = count

        if li < n-li-1:
            for ri in range(m-li-2, li, -1):
                count += 1
                matrix[ri][li] = count

    return matrix

参考答案2

direction = [
    (1, 0),
    (0, 1),
    (-1, 0),
    (0, -1)
]


def get_spiral_matrix(m, n):
    matrix = [
        [0 for ci in range(n)] for ri in range(m)
    ]

    ci, ri = -1, 0
    di = 0
    count = 0

    while count < m * n:
        dc, dr = direction[di]
        nc, nr = ci + dc, ri + dr
        if 0 <= nc < n and 0 <= nr < m:
            if matrix[nr][nc] == 0:
                count += 1
                matrix[nr][nc] = count
                ci, ri = nc, nr
                continue

        di += 1
        di %= 4

    return matrix