46. 全排列

46. 全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

　　输入: [1,2,3]
　　输出:
　　[
　　[1,2,3],
　　[1,3,2],
　　[2,1,3],
　　[2,3,1],
　　[3,1,2],
　　[3,2,1]
　　]

 

全排列：

排列的定义：从n个不同元素中，任取m(m≤n,m与n均为自然数,下同）个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；从n个不同元素中取出m(m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 A(n,m）表示。

组合：

组合的定义：从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。

计算公式： 

　　C(n,m)=C(n,n-m）。（n≥m)

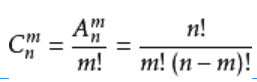
 方法一：递归

代码：

#include<iostream>
#include<bits/stdc++.h>
#include<cstring>
#include<vector>
#include<map>
using namespace std;
void Perm(int list[],int k,int m){
    //list 数组存放排列的数，K表示层 代表第几个数，m表示数组的长度
    if(k==m){
        //K==m 表示到达最后一个数，不能再交换，最终的排列的数需要输出；
        for (int i = 0; i <= m; i++)
        {
            cout<<list[i]<<" ";
        }
        cout<<endl;
    }else
    {
        for (int i = k; i <= m; i++)
        {
            swap(list[i],list[k]);
            Perm(list,k+1,m);
            swap(list[i],list[k]);
        }
    }
}

int main ()
{
    int list[]={1,2,3};
    Perm(list,0,2);
}

 

输出：

1 2 3 
1 3 2
2 1 3
2 3 1
3 2 1
3 1 2

 

方法二:使用库函数next_permutation

代码：

#include<bits/stdc++.h>
using namespace std;

int main(){
    int a[]={1,2,3};
    do{
        for (int i = 0; i <= 2; i++)
        {
            cout<<a[i]<<" ";
        }
        cout<<endl;
    }while(next_permutation(a,a+3));
}

 

输出：

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1