面试题 08.06. 汉诺塔问题

面试题 08.06. 汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例1:

　　输入：A = [2, 1, 0], B = [], C = []
　　输出：C = [2, 1, 0]
示例2:

　　输入：A = [1, 0], B = [], C = []
　　输出：C = [1, 0]

 

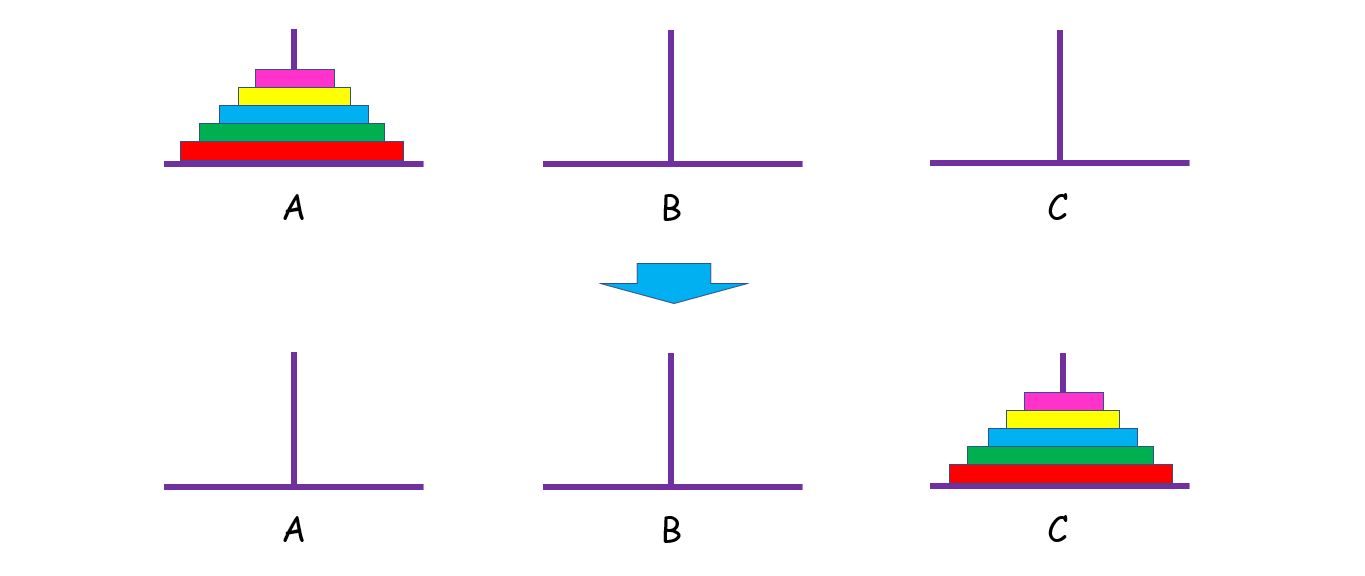
问题描述

有 A,B,C 三根柱子，A 上面有 n 个盘子，我们想把 A 上面的盘子移动到 C 上，但是要满足以下三个条件：

• 　　每次只能移动一个盘子;
• 　　盘子只能从柱子顶端滑出移到下一根柱子;
• 　　盘子只能叠在比它大的盘子上。

 

解题思路：递归与分治
这是一道递归方法的经典题目，乍一想还挺难理清头绪的，我们不妨先从简单的入手。

假设 n = 1,只有一个盘子，很简单，直接把它从 A 中拿出来，移到 C 上；

如果 n = 2 呢？这时候我们就要借助 B 了，因为小盘子必须时刻都在大盘子上面，共需要 4 步。

具体解决办法如下：

• n = 1 时，直接把盘子从 A 移到 C；
• n > 1 时，

1. 先把上面 n - 1 个盘子从 A 移到 B（子问题，递归）；
2. 再将最大的盘子从 A 移到 C；
3. 再将 B 上 n - 1 个盘子从 B 移到 C（子问题，递归）。

代码：

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        int n=A.size();
        move(n,A,B,C);

    }
    void move(int n,vector<int>&A,vector<int>&B,vector<int>&C){
        if (n==1)
        {
            C.push_back(A.back());
            A.pop_back();
            return;
        }
        move(n-1,A,C,B);// 将A上面n-1个通过C移到B
        C.push_back(A.back());// 将A最后一个移到C
        A.pop_back();       // 这时，A空了
        move(n-1,B,A,C);// 将B上面n-1个通过空的A移到C
    }
};

 

代码：

class Hanoi{
public:

    void move(int n,string from,string buffer,string to){
        if (n==1)
        {
            cout<<"from "<<from<<" to "<<to<<endl;
            return;
        }
        move(n-1,from,to,buffer);
        move(1,from,buffer,to);
        move(n-1,buffer,from,to);
    }

};

 复杂度分析：世界会毁灭吗时间复杂度：O(2^n-1)。

一共需要移动的次数。空间复杂度：O(1)。当 n = 64时，也就是有 64 个盘子的时候，如果每秒移动一个盘子，大约需要 11.8×10 

19秒...