二维差分

二维差分

我们有一个矩阵，如下图所示：

假设我们有这么一个矩阵：

1 2 4 3
5 1 2 4
6 3 5 9

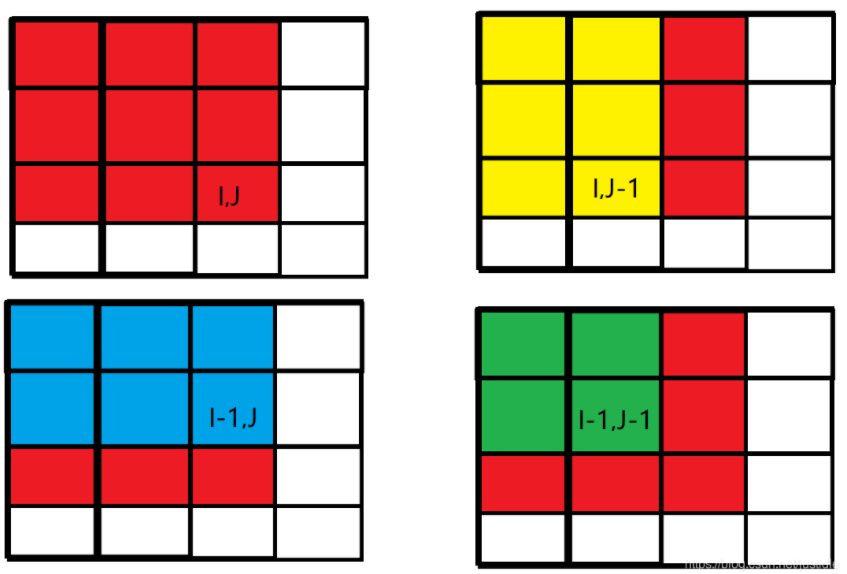
二维前缀和公式：

 sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+arr[i][j];

差分：

如果我们要在左上角是 (x1,y1)，右下角是 (x2,y2) 的矩形区间每个值都 +a，如下图所示

 在我们要的区间开始位置（x1,y1）处 +c，根据前缀和的性质，那么它影响的就是整个黄色部分，多影响了两个蓝色部分，所以在两个蓝色部分 -c 消除 +c 的影响，

而两个蓝色部分重叠的绿色部分多了个 -c 的影响，所以绿色部分 +c 消除影响。所以对应的计算方法如下：

diff[x1][y1] += c;
diff[x1][y2+1] -=c;
diff[x2+1][y1] -=c;
diff[x2+1][y2+1] += c;

差分矩阵：

diff[i][j]=arr[i][j]-arr[i-1][j]-arr[i][j-1]+arr[i-1][j-1];

差分数组为：

1 1 2 -1
4 -5 -1 3
1 1 1 2
-6 3 -2 -4

求区间值：

       要求左上角是(x1,y1),右下角是(x2,y2)的矩形区间内的值处理出前缀和后也可以O(1)时间内求出来。

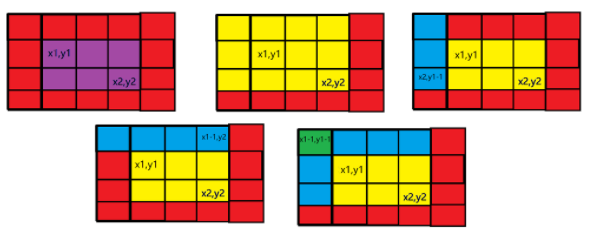
 我们要求紫色部分的值，我们已知的是黄色部分的值，但它多了两个蓝色部分的值，而两个蓝色部分有重叠了个绿色部分

sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1]

例题：

题目描述

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1，y1，x2，y2，c，其中 (x1, y1) 和 (x2, y2) 表示一个子矩阵的左上角坐标和右下角坐标。 
每个操作都要将选中的子矩阵中的每个元素的值加上 c。 
请你将进行完所有操作后的矩阵输出。

输入

第一行包含整数 n，m，q。 
接下来 n 行，每行包含 m 个整数，表示整数矩阵。 
接下来 q 行，每行包含 5 个整数 x1，y1，x2，y2，c，表示一个操作。 

输出

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

代码：

#include<bits/stdc++.h>
#include<algorithm>
#include<cstring>
using namespace std;


const int MAXN = 1e3+6;
const int MAXM = 1e3+6;
int a[MAXN][MAXM] = {};
int diff[MAXN][MAXM] = {};
 
int main() {
    int n,m,q;
    freopen("data1.txt","r",stdin);
    cin>>n>>m>>q;
    int i, j;
    for (i=1; i<=n; i++) {
        for (j=1; j<=m; j++) {
            cin>>a[i][j];
            diff[i][j] = a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
        }
    }
    for (i=0; i<q; i++) {
        int x1, y1, x2, y2, c;
        cin>>x1>>y1>>x2>>y2>>c;
        diff[x1][y1] += c;
        diff[x1][y2+1] -=c;
        diff[x2+1][y1] -=c;
        diff[x2+1][y2+1] += c;
    }
    for (i=1; i<=n; i++) {
        for (j=1; j<=m; j++) {
            diff[i][j] += diff[i-1][j]+diff[i][j-1]-diff[i-1][j-1];
            cout<<diff[i][j]<<" ";
        }
        cout<<endl;
    }
    return 0;
}