中国剩余定理

中国剩余定理

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。

《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

换句话说：“一个正整数除以3余2，除于5余3，除于7余2，求这个正整数是几？”

基本解法：

1）先找到除以3余2，除于7余2的数是那些。经过分析得到满足要求的数是21的倍数加2。

       2，23，44，65，96，107，........

2）在上述结果中继续寻找除以5余3的数。

3）满足上述要求的正整数是：23，128，233，338

这里 128-23=105  正好是[3,5,7]的最小公倍数

古人的解法：

先找5和7的公倍数中除以3余1的数：70

再找3和7的公倍数中除以5余1的数：21

再找3和5的公倍数中除以7余1的数：15

70*2+21*3+15*2=233

233-105=128

128-105=23

所以这个正整数最小是23.

 

先考虑问题的分解：

问题1：计算一个整数  ，使得它满足除以3余2、除以5余3、除以7余2。

如果能够找到三个整数  ，使得：

 除以3余2、除以5余0、除以7余0；

 除以3余0、除以5余3、除以7余0；

 除以3余0、除以5余0、除以7余2；

那么令  ，就很容易验证这时的  就满足除以3余2、除以5余3、除以7余2。

分别称找到整数  的问题为问题1-1、问题1-2、问题1-3。可以看出这三个问题本质上是类似的。

 

 

普通的中国剩余定理要求所有的互素，那么如果不互素呢，怎么求解同余方程组？

　　这种情况就采用两两合并的思想，假设要合并如下两个方程：

　　那么得到：

　　我们需要求出一个最小的xx使它满足：

　　那么x1x1和x2x2就要尽可能的小，于是我们用扩展欧几里得算法求出x1x1的最小正整数解，将它代回a1+m1x1，得到x的一个特解x′，当然也是最小正整数解。

　　所以xx的通解一定是x′加上lcm(m1,m2)∗k，这样才能保证x模m1和m2的余数是a1和a2。由此，我们把这个x′x′当做新的方程的余数，把lcm(m1,m2)当做新的方程的模数。（这一段是关键）

　　合并完成：

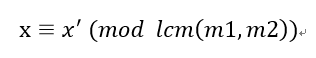
代码：

#include<bits/stdc++.h>
using namespace std;
int const MAXN=10010;
int x,y;
int k;//k组同余方程
int a[MAXN];//每个同余方程的余数
int b[MAXN];//每个同余方程的模数
int ans;
int lcm=1;
void exgcd(int a,int b)
{
    if(b==0){x=1;y=0;}
    else{
        exgcd(b,a%b);
        int tmp=x;
        x=y;
        y=tmp-a/b*y;
    }
    return;
}
int main()
{
   cin>>k;
    for(int i=1;i<=k;++i)
        cin>>b[i]>>a[i];

    for(int i=1;i<=k;++i)
        lcm*=b[i];
    for(int i=1;i<=k;++i)
    {
        exgcd(lcm/b[i],b[i]);
        x=(x%b[i]+b[i])%b[i];

        ans=(ans+(lcm/b[i])*x*a[i])%lcm;
    }

    cout<<ans;
}