迭代加深搜索
为什么需要迭代加深?
先来上发讲解图:
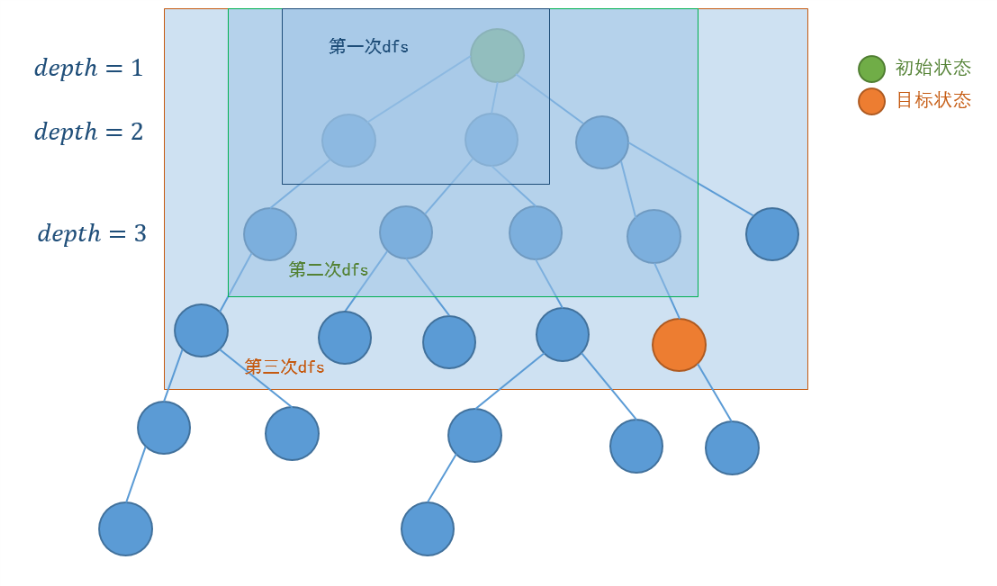
迭代加深搜索
迭代加深搜索(Iterative Deepening Depth First Search,IDDFS),是朴素深度优先搜索(Depth First Search,DFS)的一种改进。它的核心思想是:控制当前搜索的深度上限
mxd,初始化为1,并令其不断递增,在这个深度限制上进行DFS
基本思想:以BFS的思想写DFS。
理解就是以BFS的思想写DFS。首先深度优先搜索k层,若没有找到可行解,再深度优先搜索k+1层,直到找到可行解为止。
由于深度是从小到大逐渐增大的,所以当搜索到结果时可以保证搜索深度是最小的。这也是迭代加深搜索在一部分情况下
可以代替广度优先搜索的原(还比广搜省空间)。
前提:
题目一定要有解,否则会无限循环下去。
好处:
1.时间复杂度只比BFS稍差一点(虽然搜索k+1层时会重复搜索k层,但是整体而言并不比广搜慢很多)。
2.空间复杂度与深搜相同,却比广搜小很多。
3.利于剪枝。
举例:埃及分数
Description
在古埃及,人们使用单位分数的和(形如1/a的, a是自然数)表示一切有理数。
如:2/3=1/2+1/6,但不允许2/3=1/3+1/3,因为加数中有相同的。
对于一个分数a/b,表示方法有很多种,但是哪种最好呢?
首先,加数少的比加数多的好,其次,加数个数相同的,最小的分数越大越好。
如:
19/45=1/3 + 1/12 + 1/180
19/45=1/3 + 1/15 + 1/45
19/45=1/3 + 1/18 + 1/30,
19/45=1/4 + 1/6 + 1/180
19/45=1/5 + 1/6 + 1/18.
最好的是最后一种,因为1/18比1/180,1/45,1/30,1/180都大。
给出a,b ( 0〈a〈b〈1000 ),编程计算最好的表达方式。
Input
一行包含a,b ( 0〈a〈b〈1000 )。
Output
每组测试数据若干个数,自小到大排列,依次是单位分数的分母。
Sample Input
19 45
Sample Output
5 6 18
1 分析
此题显然可以用搜索来解决,但是它的解答树是及其庞大的。你既无法预估它的深度(加数个数),也无法预估当前深度下解答树的广度(加数大小)。此时只能通过IDDFS来求解。
2 思路
设当前最大深度限制为mxd,定义DFS函数为dfs(d,c,8a,b),其中d为当前深度,a/b为当前剩余的分数,c为满足1/c⩽a/b的最小c。
DFS的流程如下:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll a, b;
ll maxdep;
ll fm[1000010], ans[1000010];
//快读
inline ll read() {
ll x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0'; ch = getchar();}
return x * f;
}
//最大公约数
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll get_max(ll a, ll b) {for (ll i = 2; ; i++) if (a * i > b) return i;}
bool dfs(ll a, ll b, ll dep) {
bool flag = 0;
if (dep == maxdep) {
if (b % a) return 0;
fm[dep] = b / a;
if (fm[dep] < ans[dep] || ans[0] == 0) {
memcpy(ans, fm, sizeof fm);
}
return 1;
}
for (ll i = get_max(a, b); ; i++) {
if ((maxdep - dep + 1) * b <= a * i) break;
fm[dep] = i;
ll d = gcd(a * i - b, b * i);
if (dfs((a * i - b) / d, (b * i) / d, dep + 1)) flag = 1;
}
return flag;
}
int main() {
a = read(), b = read();
for (maxdep = 1; ; maxdep++) {//迭代加深
memset(fm, 0, sizeof fm);
memset(ans, 0, sizeof ans);//初始化
if (dfs(a, b, 0)) {
for (ll i = 0; i <= maxdep; i++) {
if (i == 0) printf("%lld", ans[i]);
else printf(" %lld", ans[i]);
}
return 0;
}
}
}