CCF冬令营Day1上午

可能只有这一讲的笔记了……QAQ

二维区间DP

听到名字就显然了，故略。

四边形不等式

讲解

有一类常见DP问题，通常是区间DP，转移方程都是

[large f_{i,j}=min{f_{i,k}+f_{k+1,j}+w_{i,j}} ]

显然枚举 (i,j,k) 是 (O(n^3)) 的，但是可以降低为 (O(n^2))：

将 (k:isim j) 改为 (k:c_{i,j-1}sim c_{i+1,j})。其中 (c_{i,j}) 为 (f_{i,j}) 的最优分割点。

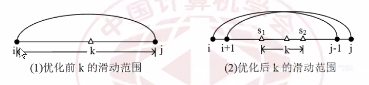
时间复杂度照例不会证明。

但是要用这个优化，需要满足四边形不等式：

[large forall i<i'le j'< j,f_{i,j'}+f_{i',j}le f_{i,j}+f_{i',j'} ]

例题：环形石子合并

轮廓线

例题

用 1X2 和 2X1 的砖块填充 NXM 的棋盘，求方案数。

数据范围：没看清

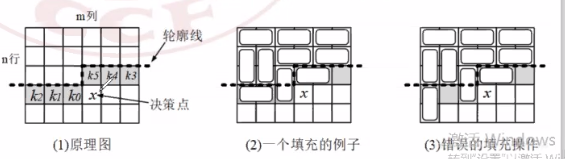
状压DP。假设我们现在是5行6列。

轮廓线上面的都填了， (k_{0sim 5}) 是否被覆盖用DP状态压缩。（就是轮廓线下面的那六个格子，注意顺序）

现在我们要下压轮廓线，

判断 (x) 状态：

1. (x) 没有砖块，那么 (k_5k_4k_3k_2k_1k_0 ightarrow k_4k_3k_2k_1k_00)

   f[now][(k<<1)&(~(1<<m))]+=f[old][k]

2. (x) 放竖砖块，那么 (k_5k_4k_3k_2k_1k_0 ightarrow k_4k_3k_2k_11 1)

   f[now][(k<<1)^1]+=f[old][k]

3. (x) 放横砖块，那么 (k_5k_4k_3k_2k_1k_0 ightarrow k_4k_3k_2k_1k_01)

   f[now][((k<<1)|3)&(~(1<<m))]+=f[old][k]

状压实现。注意 (k) 总是轮廓线下方的格子。滚动数组。

复杂度 (O(nm2^m)) 所以如果有题目 (n、m) 范围不一样，那么就考虑一下此算法。

P.S. 现在开始讲单调队列DP和背包了？？？？

多重背包单调队列优化

没听

斜率优化

假如有DP方程 (f_j=max{a_i imes b_j+f_i})

(f_j=max{a_i imes b_j+f_i})

先去掉 (max) 令 (y=f_j,x=b_j,k=a_i,b=f_i)

则变成了 (y=kx+b)。