Codeforces 314 and 315

315 C

题意

有 (n) 个元素，有 (a,d) 两个属性

(d_i) 的计算公式为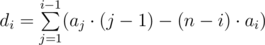

现在找到第一个满足 (d_ile k) 的元素，将其删除，重新计算其余元素的 (d_i)
重复进行此操作，直到没有可以删除的元素为止
依次输出被删除元素的编号
((1 ≤ n ≤ 2·10^5))

Examples

Input
5 0
5 3 4 1 2
Output
2
3
4
Input
10 -10
5 5 1 7 5 1 2 4 9 2
Output
2
4
5
7
8
9

解

推了很久，终于推出来了
将公式变形，每次删除掉下标为 (k) 的元素之后，其余元素的 (d_i) 的变化为：

[d_i+=a_i*(i-1)(i<k) ]

[d_i+=-sum_{j=k+1}{i-1}a_j+(n-i)*a_i-a_k*(k-1) ]

用一个sum变量维护 (sum_{j=k+1}{i-1}a_j) 部分，cnt变量维护 ((n-i)*a_i) 部分，add变量维护 (a_k*(k-1)) 部分
(O(n)) 扫即可

Code

#include<bits/stdc++.h>
#define maxn 200003
using namespace std;
long long n,cnt,k,a[maxn],d[maxn],add,sum;
int main(){
    scanf("%lld%lld",&n,&k);
    sum=0;
    for(int i=1;i<=n;i++){
        scanf("%lld",a+i);
        d[i]=sum-(i-1)*(n-i)*a[i];
        sum+=(i-1)*a[i];
    }
    sum=0;
    for(int i=1;i<=n;i++){
        if(d[i]-sum+cnt*(n-i)*a[i]-add<k){
            printf("%d
",i);
            add+=a[i]*(i-1);
            cnt++;
        }
        else{
            sum+=a[i]*cnt;
        }
    }
    return 0;
}

315 D

题意

设 ([a,b]) 表示周期为 (b) ，每个周期中的字符串为 (a) 的一个字符串
现在给你两个串 (a,b)，两个正整数 (c,d)
问满足 ([[b,d],p]) 是 ([a,c]) 的子序列的最大的 (p) 是多少
( (1le |a|,|b|le 100,1le c,dle 10^7) )

Examples

Input
10 3
abab
bab
Output
3

解

令字符串下标从一开始
维护一个 (f) 数组， (f[i]) 表示 (b[i..|b|]) 在(a) 中出现了几次
再来一个 (nxt) 数组（有一点点类似kmp）， (nxt[i]) 表示 (b) 匹配 (a) 匹配完一遍以后指 (b) 的指针指在哪个位置
最后，for(int i=1;i<=c;i++)ans+=f[pos],pos=nxt[pos];
然后手膜一遍，发现效率异常高，达到了 (O(n))

Code

#include<bits/stdc++.h>
#define maxn 103
using namespace std;
char s[maxn],t[maxn];
int a,b,n,m,f[maxn],nxt[maxn],ans,pos;
int main(){
    scanf("%d%d%s%s",&a,&b,s+1,t+1);
    n=strlen(s+1),m=strlen(t+1);
    for(int i=1;i<=m;i++){
        pos=i;
        for(int j=1;j<=n;j++){
            if(t[pos]==s[j])pos++;
            if(pos==m+1)f[i]++,pos=1;
        }
        nxt[i]=pos;
    }
    pos=1;
    for(int i=1;i<=a;i++){
        ans+=f[pos];
        pos=nxt[pos];
    }
    printf("%d
",ans/b);
    return 0;
}

315 E

题意

给你一个序列，找出该序列的所有最长非减子序列（不能有重复元素），求所有这些子序列的价值的和。
一个子序列的价值定义为该序列中所有元素的乘积
答案膜 (10^9+7)
( (1le nle 10^5,1le a_ile 10^6) )

Examples

Input
1
42
Output
42
Input
3
1 2 2
Output
13
Input
5
1 2 3 4 5
Output
719

解

设 (dp[i]) 表示枚举到第 (i) 个元素的答案
凑一凑，转移方程就能出来： (dp[i]=sum_{a[j]le a[i];and;j<i}dp[j]*a[j]+a[j])
等式右边的左侧的前缀和可以用树状数组维护
但是，不能有重复元素！！！
注意到 (a_ile 10^6)
所以我们另设一个数组 (last) ， (last[a[i]]) 表示上一个与 (a[i]) 相等的元素的 (dp) 值
把 (dp[i]) 减去 (last[a[i]]) 即可
但是，更新 (last[a[i]]) 时切记不可以直接 (last[a[i]]=dp[i]) ！！！

Code

#include<bits/stdc++.h>
#define maxn 100003
#define mod 1000000007
using namespace std;
long long dp[maxn],last[1000003],ans,a[maxn],mx,t[1000003];
int n;
void add(int pos,long long k){
    while(pos<=mx){
        t[pos]=(t[pos]+k)%mod;
        pos+=pos&-pos;
    }
}
long long query(int pos){
    long long ret=0;
    while(pos){
        ret=(ret+t[pos])%mod;
        pos-=pos&-pos;
    }
    return ret;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%lld",a+i),mx=max(mx,a[i]);
    for(int i=1;i<=n;i++){
        dp[i]=(mod+(query(a[i])*a[i]%mod+a[i])%mod-last[a[i]])%mod;
        last[a[i]]=(query(a[i])*a[i]%mod+a[i])%mod;
        ans=(ans+dp[i])%mod;
        add(a[i],dp[i]);
    }
    printf("%lld
",ans);
    return 0;
}

314 D

题意

平面上有 (n) 个点，现在有两条直线，互相垂直，与 (x) 轴呈 (45°) 角，定义 (dis(i)) 为点 (i) 到两条直线的曼哈顿距离（ (|x_1-x_2|+|y_1-y_2|) ）中较小的一个
移动两条直线使得 (max{dis(i)}) 最小
( (1le nle 10^5) )

Examples

Input
4
0 0
2 0
0 2
2 2
Output
0.000000000000000
Input
4
1 0
0 1
2 1
1 2
Output
1.000000000000000

解

发现点 (i) 到某条直线的曼哈顿距离必定是点 (i) 到这条直线的距离的 (sqrt{2}) 倍。
所以我们将整个坐标轴旋转 (45°) ，这样，原来坐标为 ((x,y)) 的点变成了 ((x-y,x+y)) ，而且坐标还是整数（long long即可解决）。
问题转化为求两条分别与x轴、y轴平行的直线
将点按x坐标排序
然后我们二分 (max{dis(i)})
设二分出的值为mid
用两个指针维护距离至多为2mid的两条平行于y轴的直线
两条直线中间的点一定是合法的
问题在于两条直线之外的点
其实，只要两条直线之外的点y坐标最大值减最小值是小于等于2mid的，我们就构造出了一种可行解，return true
前缀、后缀的最大值、最小值可以先预处理出来

Code

#include<bits/stdc++.h>
#define maxn 100003
#define INF 100000000000000000ll
using namespace std;
struct point{
    long long x,y;
    point(){}
    point(long long _x,long long _y):x(_x),y(_y){}
    bool operator <(const point& p)const{return x==p.x?y<p.y:x<p.x;}
};

point a[maxn];
int n;
long long mx1[maxn],mi1[maxn],mx2[maxn],mi2[maxn];
bool check(long long M){
    for(int i=1,j=1;i<=n;i++,j=max(i,j)){
        while(j<=n&&a[j].x-a[i].x<=M)j++;j--;
// printf("i:%d j:%d
",i,j);
        if(max(mx2[j+1],mx1[i-1])-min(mi2[j+1],mi1[i-1])<=M)return 1;
    }
    return 0;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        long long x,y;
        scanf("%lld%lld",&x,&y);
        a[i]=point(x-y,x+y);
    }
    sort(a+1,a+n+1);
    mx1[0]=mx2[n+1]=-INF,mi1[0]=mi2[n+1]=INF;
    for(int i=1;i<=n;i++){
        mx1[i]=max(mx1[i-1],a[i].y);
        mi1[i]=min(mi1[i-1],a[i].y);
    }
    for(int i=n;i>=1;i--){
        mx2[i]=max(mx2[i+1],a[i].y);
        mi2[i]=min(mi2[i+1],a[i].y);
    }
    long long l=0,r=4000000000ll,mid,ans=r;
    while(l<=r){
        mid=(l+r)>>1;
        if(check(mid))ans=mid,r=mid-1;
        else l=mid+1;
    }
    printf("%.12lf
",ans*0.5);
    return 0;
}