求解时间复杂度递归式

（一）主定理

对于 (T(N)=a*T(N/b)+Theta(N^d))
且(T(1))为常数，有

1. (log_b a>d Rightarrow) 复杂度为 (Theta(N^{log_b a}))

2. (log_b a=d Rightarrow) 复杂度为 (Theta(N^d* log N))

3. (log_b a<d Rightarrow) 复杂度为 (Theta(N^d))

加强版

以下 (O(N)) 为复杂度上界， (Theta(N)) 为复杂度确界， (Omega(N)) 为复杂度下界。

对于 (T(N)=a*T(N/b)+f(N))
且(T(1))为常数，有

1. (f(N)=O(N^d),log_b a>d Rightarrow) 复杂度为 (Theta(N^{log_b a}))

2. (f(N)=Theta (N^d log^k n),kgeq 0,log_b a=d Rightarrow) 复杂度为 (Theta(N^d log^{k+1} N))

3. (f(N)=Omega (N^d),log_b a<d Rightarrow) 复杂度为 (Theta(N^d))

例题

（以下(T(1))都为常数）

1. 设某算法时间复杂度可表示为(T(n)=9T(n/3)+n^2)，求该算法时间复杂度。

解：

由题意得：(a=9,b=3,d=2)
所以(log_ba=log_39=2=d)
所以是第二种情况，复杂度为(Theta(n^2log n))

2. 设某算法时间复杂度可表示为(T(n)=T(2n/3)+n)，求该算法时间复杂度。

解：

由题意得：(a=1,b=frac{3}{2},d=1)
所以(log_ba=log_{frac{3}{2}}1=0<d=1)
所以是第三种情况，复杂度为(Theta(n))

3. 设某算法时间复杂度可表示为(T(n)=3T(sqrt n)+log n)，求该算法时间复杂度。

解：

(T(n)=3T(n^{frac{1}{2}})+log n)

(Leftrightarrow T(2^n)=3T(2^{frac{n}{2}})+n)

设(t(n)=T(2^n))，则(t(n)=3t(n/2)+n)

由题意得：(a=3,b=2,d=1)
所以(log_ba=log 3≈1.58>d=1)
所以是第三种情况，(t(n))的复杂度为(O(n^{log 3}))
所以(T(n))的复杂度为(Theta(log^{log 3}n))。

4. 设某算法时间复杂度可表示为(T(n)=2T(n/5)+log n)，求该算法时间复杂度。

解：

易得(log n)的一个上界是(Theta(n^k)(0<k<log_5 2))，那么是第一种情况，(T(n))的复杂度为(Theta(n^{log_5 2}))。

---

（二）递归树

考虑递归式$$T(n)=2T(n/2)+n^2$$
可将其化为$$T(n)=T(n/2)+T(n/2)+n^2$$
于是可以画一棵递归树，对于一个节点，节点的值为非函数项，再将式中每一个函数项向下迭代，式中有几个函数项，递归树就是几叉树，且有(log n)层，把每一行所有节点的和写在右边，如下图所示。

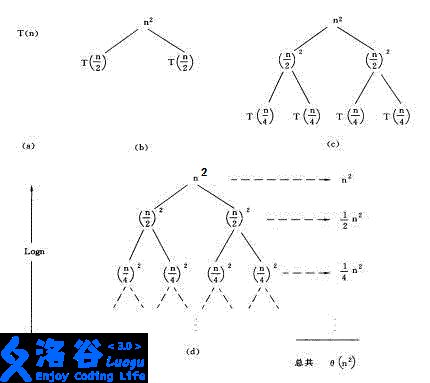
然后，右边所有数之和（一个含(n)的表达式）即为该式的复杂度。

如图，该图中右边所有数之和为$$(1+frac{1}{2}+(frac{1}{2})^{2+(frac{1}{2})}3+...)* n²⁼²ⁿ2$$

所以，(T(n)=T(n/2)+T(n/2)+n^2)的时间复杂度为(Theta(n^2))

例题

1. 计算递归式(T(n)=T(n/3)+T(2n/3)+n)的复杂度。

解：

递归树如下图所示

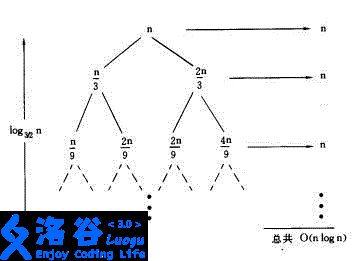
右边所有数之和为$$(log_{frac{3}{2}}n+1)*n$$

所以，(T(n))的时间复杂度为(Theta(nlog n))