xj膜你赛26

人生赢家

每次生成一个 ([0,n)) 的随机整数，如果这个随机数和给出的 (m) 个数字中的其中一个数字相等，
那么就停止生成随机数，否则继续生成，求出所有生成的数的和的期望。

输入

第一行两个正整数 (n,m)，
第二行 (m) 个整数 表示障碍，保证两两不同。

输出

输出一行一个实数表示期望，保留 (6) 位小数，

输入输出样例

2 1
1

1.000000

数据范围

(nle 10^7,1le mle n,0le a_ile n-1)

分析

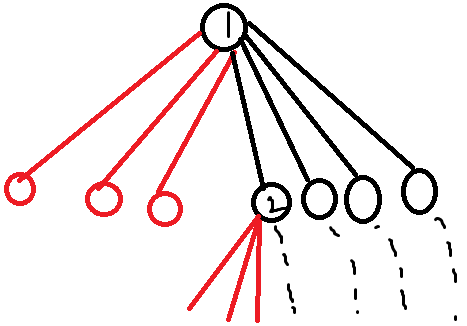
上图中的红色节点表示给出的随机数等于 (m) 个数字之一，停止生成；黑色节点表示需要继续生成。
我们发现，图中的 (1) 号节点和 (2) 号节点状态相同，因此答案一定完全一致。
设 (ans) 表示节点 (1) 的答案， (sum_1) 表示 (m) 个数的和， (sum_2) 表示(n)个数的总和 (-m) 个数的和，则 $$ans=frac{1}{n}sum_1+frac{1}{n}sum_2+frac{1}{n}mans=frac{n(n-1)}{2*m}$$
然后发现 (10^7) 的数据一点用都没有
还有，本题卡精度

Code

#include<cstdio>
using namespace std;
int read(){
    char c=getchar();
    bool sgn=0;
    int x=0;
    while((c<'0'||c>'9')&&c!='-')c=getchar();
    if(c=='-')sgn=1,c=getchar();
    while(c>='0'&&c<='9'){
        x=(x<<3)+(x<<1)+c-'0';
        c=getchar();
    }
    return sgn?-x:x;
}
char tmp[1000];
int main(){
    long long n=read(),m=read();
//以下代码仅用于输出(n*(n-1))/(2*m)
    n=n*(n-1)/2;
    printf("%lld",n/m);
    n%=m;
    sprintf(tmp,"%.6lf",double(n)/m);
    printf(tmp+1);
    return 0;
}

虐暴全场

众所周知，DH 是一位人生赢家，他不仅能虐暴全场，而且还正在走向人生巅峰；
一天，DH 在刷题的时候碰到了一道大模拟题：
二维坐标上有一些点，保证它们的 x 坐标互不相同，（y 坐标可能相同，可能有 3 点共线），
每个点都有一个权值 ，表示点 i 指向点 ，初始时每个点指向它自己，
模拟过程就是执行以下伪代码：

for i=1 to n do b[i]=i
for i=1 to n do
{
    输出 b[i];
    if（b[i]不等于 i）L=连接点 i，b[i] 的直线；
    else L=过点 i 平行于 x 轴的直线；
    对于任意的 x，满足点 x 在直线 L 下方（且不在直线上），b[x]=i;
}

DH 表示他要赶着去干人生赢家应该干的事并把这道题扔给了你。

输入

第一行给出正整数 (n)，
接下来有 (n) 行，每行两个正整数 ，表示第 (i) 个点的坐标。

输出

(n) 行 (n) 个数，表示模拟过程中你输出的 (n) 个 (b_i)。

输入输出样例

7
1 10
2 7
3 8
4 2
5 6
6 100
7 10

1
1
1
3
1
6
6

数据范围

(n,mle 10^6,max{x_i},max{y_i}le 10^9,x_i)为单调递增以保证互不相同

分析

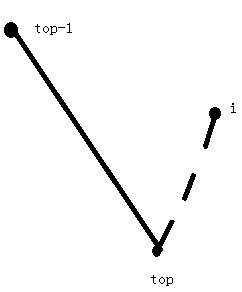
我们维护一个类似凸包的东西，设栈顶元素为 (top) ，对于一个新点 (i) ，如果 (y_i>y_top) ，那么 (top) 就没有任何用处，以后的点最多只会连 (i) ，不可能会连 (top) ，所以弹出 (top)；
之后，如果出现下面这种情况，也弹出 (top) ，因为以后的点最多只会连 (i) ，不可能会连 (top) 。

Code

#include<cstdio>
#define maxn 1000002
using namespace std;
template<typename tp>
tp read(){
    tp x=0;
    bool sgn=0;
    char c=getchar();
    while((c<'0'||c>'9')&&c!='-')c=getchar();
    if(c=='-')sgn=1,c=getchar();
    while(c>='0'&&c<='9'){
        x=(x<<3)+(x<<1)+c-'0';
        c=getchar();
    }
    return sgn?-x:x;
}
template<typename tp>
void write(tp x){
    if(x<0)putchar('-'),write(-x);
    else{
        if(x>=10)write(x/10);
        putchar(x%10+'0');
    }
}
struct point{
    long long x,y;
    point(){}
    point(long long X,long long Y):x(X),y(Y){}
    const point operator -(const point& p)const{
        return point(x-p.x,y-p.y);
    }
}pnt[maxn];
long long cross(const point& p,const point& q){
    return p.x*q.y-p.y*q.x;
}
int st[maxn],top;
int main(){
    int n=read<int>();
    for(int i=1;i<=n;i++){
        pnt[i].x=read<long long>(),pnt[i].y=read<long long>();
        while(top>=1&&pnt[i].y>=pnt[st[top]].y)top--;
        while(top>=2&&cross(pnt[i]-pnt[st[top]],pnt[st[top]]-pnt[st[top-1]])<=0)top--;
        if(top)write(st[top]);
        else write(i);
        putchar('
');
        st[++top]=i;
    }
    return 0;
}