题目大意:见刘汝佳《算法竞赛入门经典——训练指南》P173。
解题思路:
问题可以转化为求共有多少条过点阵中的点的斜线。其中必定包含左斜线和右斜线,由于点阵式对称的,所以我们只需求出左右斜线中的一种的总数,乘2就可以得到答案。
我们先求出各点到其左上角的只经过两个点的左斜线的总数 cnt ,那么答案就是所有点的 cnt 的总和去掉其中重复计算的数值。设点阵上某点坐标为(i,j),则这个子问题可以转化为求 [ 1,i ] 和 [ 1,j ] 中互质的数对的个数。简单解释:对于点(i,j),若 gcd(i,j)=1,则该点到(0,0)的直线必定只经过此二点;否则你必定可以找到 x=i/gcd(i,j),y=j/gcd(i,j),(i,j)到(0,0)的直线经过(x,y)。而对于该点到左上角其他点(除了(0,0))的只经过两个点的直线,可以通过 [ 1,i ) 和 [ 1,j )中各点到(0,0)的只经过两个点的直线平移得到(如图1所示)。递推式为:cnt[i][j] = cnt[i-1][j] + cnt[i][j-1] - cnt[i-1][j-1] + (gcd(i,j)==1?1:0)。
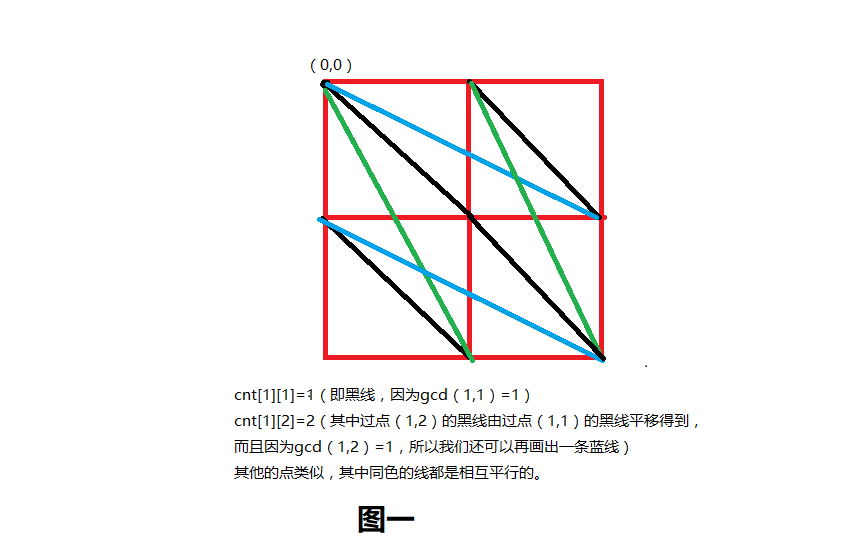
现在来算最终答案 ans 。很自然的得出:ans[i][j] = ans[i-1][j] + ans[i][j-1] - ans[i-1][j-1] + cnt[i][j]。但这么计算会有一个重复:在 cnt[i][j] 中包含了 cnt[i/2][j/2] ,所以要再减去 cnt[i/2][j/2]。over.
AC代码:
1 #include <cstdio> 2 using namespace std; 3 const int maxn=302; 4 int cnt[maxn][maxn],ans[maxn][maxn]; 5 int gcd(int a,int b){ 6 if (b == 0) return a; 7 return gcd(b, a%b); 8 } 9 void init(){ 10 for(int i=1;i<maxn;i++){ 11 for(int j=1;j<maxn;j++){ 12 cnt[i][j]=cnt[i-1][j]+cnt[i][j-1]-cnt[i-1][j-1]+(gcd(i,j)==1?1:0); 13 } 14 } 15 for(int i=1;i<maxn;i++){ 16 for(int j=1;j<maxn;j++){ 17 ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1]+cnt[i][j]-cnt[i/2][j/2]; 18 } 19 } 20 } 21 int main(){ 22 init(); 23 int n,m; 24 while(scanf("%d%d",&n,&m)==2&&n&&m){ 25 printf("%d ",ans[n-1][m-1]*2); 26 } 27 return 0; 28 }