数轴上n<=500000个点,点i在Xi处有Ai个东西,Xi递增,每秒钟可移动一单位并瞬间拿或放一个东西,最多能同时拿一个东西,任选择一个点在T<=1e18秒内把尽可能多的东西拿到该点。
感谢KPM大佬提供的解法!方便快捷!
最优方案一定是在这n个点上,因此枚举点看如何计算最优答案。
越往右边的点取到的最多点数的区间不一定越往右,如图: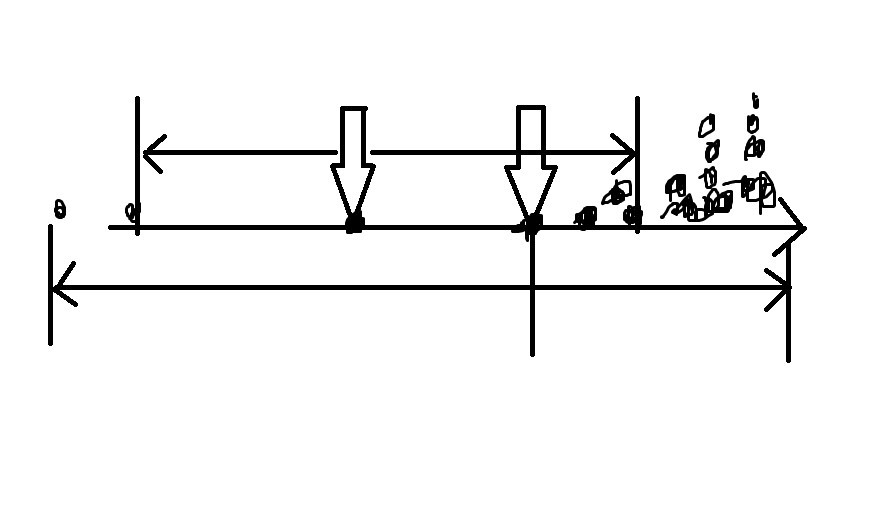
上图中,选择的点向右移动后,拿到右边一堆点的代价变小,从而可以拿到左边更远的点,因此排除单调性,考虑二分。
可以发现到最优情况下到左右走的最大的路程总长度(是路程的总长度)是一样的,但如果二分长度还要再二分找到与长度对应的点,复杂度难以接受。
因此直接在左右两边分别二分点下标,直接统计答案,再判定完一次后,如果该次判定成功,那么更新答案后,把离枚举的点近的一边往远处二分;失败则把离枚举的点远的一边往近处二分。
这样会有两个小问题。一,存在最优方案不一定要取完某个点上的所有东西。因此判断时,看T是否落在 最远的点只取一个 到 最远的点全部取 这两个答案之间,如果是就最远的点取部分,T大了就全取,T小了就不更新答案。二,当一边停止二分时,另一边应继续二分下去,这里需要很多的判断,见代码。

1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 #include<algorithm> 5 //#include<iostream> 6 using namespace std; 7 8 #define LL long long 9 int n;LL T; 10 #define maxn 500011 11 LL x[maxn],a[maxn],sumax[maxn],suma[maxn]; 12 void right(int &l,int r,int mid) {l=r==mid?r:mid+1;} 13 void left(int l,int &r,int mid) {r=l==mid?l:mid-1;} 14 int main() 15 { 16 scanf("%d%lld",&n,&T);T>>=1; 17 for (int i=1;i<=n;i++) scanf("%lld",&x[i]); 18 LL ans=0; 19 for (int i=1;i<=n;i++) scanf("%lld",&a[i]),ans=max(ans,a[i]); 20 sumax[0]=suma[0]=0; 21 for (int i=1;i<=n;i++) 22 { 23 sumax[i]=sumax[i-1]+x[i]*a[i]; 24 suma[i]=suma[i-1]+a[i]; 25 } 26 for (int i=1;i<=n;i++) 27 { 28 int ll=1,lr=i,rl=i,rr=n; 29 while (ll<=lr && rl<=rr) 30 { 31 int lmid=(ll+lr)>>1,rmid=(rl+rr+1)>>1; 32 LL sl=x[i]-x[lmid],sr=x[rmid]-x[i]; 33 LL whole=(suma[i]-suma[lmid-1])*x[i]-(sumax[i]-sumax[lmid-1])+(sumax[rmid]-sumax[i])-(suma[rmid]-suma[i])*x[i]; 34 LL sing=whole-(sl<sr?sr*(a[rmid]-1):sl*(a[lmid]-1)); 35 if (T<sing) 36 { 37 if (ll==lr && rl<rr) left(rl,rr,rmid); 38 else if (ll<lr && rl==rr) right(ll,lr,lmid); 39 else if (ll<lr && rl<rr) 40 { 41 if (sl<sr) left(rl,rr,rmid); 42 else right(ll,lr,lmid); 43 } 44 else break; 45 } 46 else 47 { 48 if (max(sl,sr) && sing<=T && T<=whole) 49 { 50 LL tmp=(sl<sr?suma[rmid-1]-suma[lmid-1]+(T-sing)/sr+1:suma[rmid]-suma[lmid]+(T-sing)/sl+1); 51 ans=max(ans,tmp); 52 } 53 else if (T>whole) ans=max(ans,suma[rmid]-suma[lmid-1]); 54 if (ll==lr && rl<rr) right(rl,rr,rmid); 55 else if (ll<lr && rl==rr) left(ll,lr,lmid); 56 else if (ll<lr && rl<rr) 57 { 58 if (sl<sr) left(ll,lr,lmid); 59 else right(rl,rr,rmid); 60 } 61 else break; 62 } 63 } 64 } 65 printf("%lld ",ans); 66 return 0; 67 }
