BZOJ1742: [Usaco2005 nov]Grazing on the Run 边跑边吃草

数轴上n<=1000个点，从p出发以任意顺序走到所有的点，求到达每个点的时间之和的最小值。

好题！看起来水水的实际易错！

显然的结论是经过一个区间点之后肯定落在左端点或右端点上，谁没事最后还往中间跑呢！那就可以拍个序然后设计dp状态了，一个区间dp，f[i,j,0/1]表示走了区间i~j，最后落在左/右端点。

一个小技巧是把p算成一个点，初始化时之后p这个状态为0，其他都inf。那么问题来了！

方法一：记到状态的时间t[i,j,0/1]，那么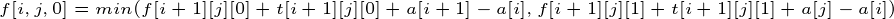，相应更新t，其他同理。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
//#include<iostream>
using namespace std;
 
int n,p;
#define maxn 1011
int a[maxn],f[maxn][maxn][2],t[maxn][maxn][2];
const int inf=0x3f3f3f3f;
int min(int a,int b) {return a<b?a:b;}
int main()
{
    scanf("%d%d",&n,&p);
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    sort(a+1,a+1+n);
    for (int i=1;i<=n;i++) f[i][i][0]=f[i][i][1]=t[i][i][0]=t[i][i][1]=inf;
    a[n+1]=inf;int pos;
    for (pos=1;pos<=n+1;pos++) if (a[pos]>p) break;
    if (pos==n+1) t[n][n][0]=t[n][n][1]=f[n][n][0]=f[n][n][1]=p-a[n];
    else if (pos==1) t[1][1][0]=t[1][1][1]=f[1][1][0]=f[1][1][1]=a[1]-p;
    else f[pos][pos][0]=f[pos][pos][1]=a[pos]-p,f[pos-1][pos-1][0]=f[pos-1][pos-1][1]=p-a[pos-1],
         t[pos][pos][0]=t[pos][pos][1]=a[pos]-p,t[pos-1][pos-1][0]=t[pos-1][pos-1][1]=p-a[pos-1];
    for (int len=1;len<n;len++)
        for (int i=1;i<=n-len;i++)
        {
            const int j=i+len;
            if (f[i+1][j][0]+t[i+1][j][0]+a[i+1]-a[i]<f[i+1][j][1]+t[i+1][j][1]+a[j]-a[i])
            {
                t[i][j][0]=t[i+1][j][0]+a[i+1]-a[i];
                f[i][j][0]=f[i+1][j][0]+t[i][j][0];
            }
            else
            {
                t[i][j][0]=t[i+1][j][1]+a[j]-a[i];
                f[i][j][0]=f[i+1][j][1]+t[i][j][0];
            }
            if (f[i][j-1][0]+t[i][j-1][0]+a[j]-a[i]<f[i][j-1][1]+t[i][j-1][1]+a[j]-a[j-1])
            {
                t[i][j][1]=t[i][j-1][0]+a[j]-a[i];
                f[i][j][1]=f[i][j-1][0]+t[i][j][1];
            }
            else
            {
                t[i][j][1]=t[i][j-1][1]+a[j]-a[j-1];
                f[i][j][1]=f[i][j-1][1]+t[i][j][1];
            }
            f[i][j][0]=min(f[i][j][0],inf);
            f[i][j][1]=min(f[i][j][1],inf);
        }
    printf("%d
",min(f[1][n][0],f[1][n][1]));
    return 0;
}

错误！递推式不成立，没有考虑当前决策对后续状态的影响。错误样例？自己找个标程对拍吧！

方法二：直接把状态对后面的影响算出来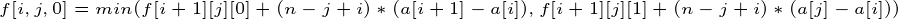，，保证了无后效性。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
//#include<iostream>
using namespace std;

int n,p;
#define maxn 1011
int a[maxn],f[maxn][maxn][2];
const int inf=0x3f3f3f3f;
int min(int a,int b) {return a<b?a:b;}
int main()
{
    scanf("%d%d",&n,&p);
    for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    a[++n]=p;
    sort(a+1,a+1+n);
    for (int i=1;i<=n;i++)
    {
        if (a[i]!=p) f[i][i][0]=f[i][i][1]=inf;
        else f[i][i][0]=f[i][i][1]=0;
    }
    for (int len=1;len<n;len++)
        for (int i=1;i<=n-len;i++)
        {
            const int j=i+len;
            f[i][j][0]=min(inf,min(f[i+1][j][0]+(n-j+i)*(a[i+1]-a[i]),f[i+1][j][1]+(n-j+i)*(a[j]-a[i])));
            f[i][j][1]=min(inf,min(f[i][j-1][0]+(n-j+i)*(a[j]-a[i]),f[i][j-1][1]+(n-j+i)*(a[j]-a[j-1])));
        }
    printf("%d
",min(f[1][n][0],f[1][n][1]));
    return 0;
}

 此题在九月份错过一次。

BZOJ1694一样哦！然而又错了，一看原题一激动忘排序了。