BZOJ1775: [Usaco2009 Dec]Vidgame 电视游戏问题

n<=50个游戏机有花费，每个游戏机有Gi<=10种游戏，每种游戏有花费有收益，买了游戏机才能玩对应游戏，求最大收益。

这就是一个背包！不过有依存关系，就不会了！

方法一：f[i][j]表示游戏机i用j块钱能得多少收益，这是可以预处理的，而g[i][j]表示前i个游戏机用j块钱最大收益，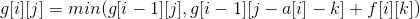

果断tle，究其原因在于g[i][j]的转移，本来一个游戏机没几款游戏，转移10次就够了，被我搞成钱，搞了那么多次。

方法二：与上相同，但k和f[i][k]改成那十个游戏数的值。没了。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
//#include<iostream>
using namespace std;
 
int n,m;
#define maxn 100011
struct Start{int v,cnt;}p[maxn];
int v[55][23],w[55][23];
int f[2][maxn],cur;
int main()
{
    scanf("%d%d",&n,&m);
    for (int i=1;i<=n;i++)
    {
        scanf("%d%d",&p[i].v,&p[i].cnt);
        for (int j=1;j<=p[i].cnt;j++) scanf("%d%d",&w[i][j],&v[i][j]);
    }
    cur=0;memset(f,0,sizeof(f));
    for (int i=1;i<=n;i++)
    {
        cur^=1;
        for (int j=0;j<p[i].v;j++) f[cur][j]=0;
        for (int j=p[i].v;j<=m;j++) f[cur][j]=f[cur^1][j-p[i].v];
        for (int j=1;j<=p[i].cnt;j++)
            for (int k=m;k>=p[i].v+w[i][j];k--)
                f[cur][k]=max(f[cur][k],f[cur][k-w[i][j]]+v[i][j]);
        for (int j=0;j<=m;j++) f[cur][j]=max(f[cur^1][j],f[cur][j]);
    }
    printf("%d
",f[cur][m]);
    return 0;
}