n<=300000个点的树,每个点有个人于第Ti秒观测,有m<=300000个人于时间0开始从Sj跑到Tj,速度1个点每秒,输出每个点上的人观察到的跑步的人的数量。
前25分:直接模拟每条路径,先s跑到lca再跑到t,边跑边记时间,如果经过某个点时时间刚好一样就该点答案++。
Si等于1的20分:观察人能观察到,只有他观察的时间和深度相等的时候。而一个跑步人跑下来就是这条链上满足“观察时间等于深度”的点答案+1,这可以用一个差分标记解决,如下图。
这样,最后从根节点开始向下dfs,一路上把标记加上,满足“观察时间等于深度”的点的答案就是当前的标记,而其他的点答案为0。
树变成一条链的15分:这启发着我们去追寻观察人的信息和跑步人的信息的关系。若有个人从Si跑到Ti,那么观测点j能观测到的条件就是j-Si=Wj且j<=Ti。那就是找j-Wj=Si的。类似于刚才的差分标记,把一个Si->Ti记两个标记,在Si处把数组中下标Si++,在Ti+1处--,扫过来的时候,把标记处理完,再查找下标j-Wj的点有几个,就可以直接回答询问。
最后的分:其实会以上这些,再不写正解就可惜了,因为推导的过程都差不多,方法也差不多。现在来看一个路径: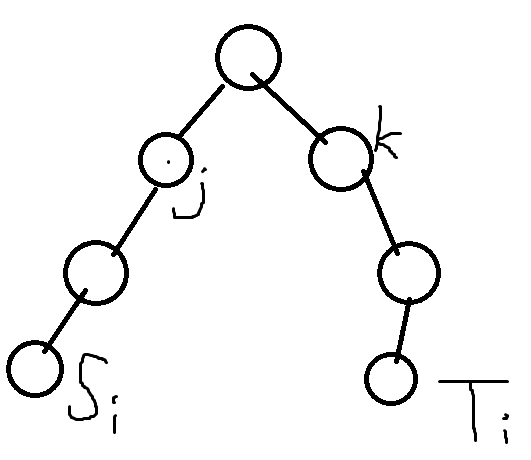
一个路径其实就一上一下两个过程,在向上经过j点时观察到的条件是:dep(Si)-dep(j)=Wj,dep()表示深度,Wj为观测时间。接下来到k那边和Si就无关了,但与之相关的Ti:dep(Ti)-dep(k)=Li-Wk,其中Li表示路径i的长度,也就是到Ti的时间,这段时间差恰好等于Ti到k的长度时可以观测到。整理两个式子,dep(Si)=dep(j)+Wj,dep(Ti)-Li=dep(k)-Wk。这么看来,回答一个询问,实际上是找这个观测点的子树里有多少个i满足上面两个式子。
不过这样是有偏差的。例如这样:
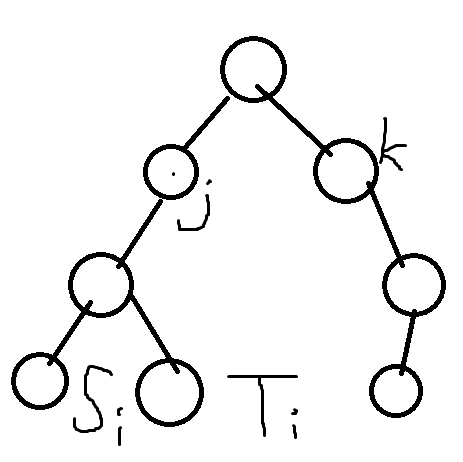
Si和Ti尽管是j的子树内的点,但他们对答案没影响。而j的孩子点,Si和Ti在这里会被计算两次。也就是要想个办法把Si和Ti能影响的范围表示出来。
可以发现,根据dfs的顺序,如果在Si处把对应信息+1,Ti处+1,那么在lca(Si,Ti)处应-1,lca的父亲那里再-1,这样一来,就可以使得Si到Ti的路径上每个点统计答案时只算到他们一次。
也就是说,开A,B两个数组存dep(j)+Wj和dep(j)-Wj两种信息,把一个跑步人拆成四个信息变化:在Si处,A数组中信息点dep(Si)加一;在Ti处,B数组中信息点dep(Ti)-Li加一;在lca(Si,Ti)处,A数组中信息点dep(Si)减一;在lca的父亲那里,B数组中信息点dep(Ti)-Li减一。信息点的变化以邻接表的形式连在它应该在的位置,在访问一棵子树时,先遍历子树,再把这个点的所有信息点变化处理好,然后在A,B两个数组中直接查对应值dep(j)+Wj,dep(j)-Wj的信息,这个信息就是答案。
具体见代码。由于B数组里的信息点涉及减法,故把B数组里的值都加上了n,查询时也加上n即可。

1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #include<algorithm> 5 //#include<iostream> 6 using namespace std; 7 8 int n,m; 9 #define maxn 300011 10 struct Edge{int to,next;}edge[maxn*2];int first[maxn],le=2; 11 int dep[maxn],fa[maxn][22]; 12 void in(int x,int y) {Edge &e=edge[le];e.to=y;e.next=first[x];first[x]=le++;} 13 void insert(int x,int y) {in(x,y);in(y,x);} 14 void dfs(int x,int f) 15 { 16 dep[x]=dep[f]+1;fa[x][0]=f; 17 for (int i=first[x];i;i=edge[i].next) 18 { 19 const Edge &e=edge[i]; 20 if (e.to!=f) dfs(e.to,x); 21 } 22 } 23 void makef() 24 { 25 for (int j=1;j<=20;j++) 26 for (int i=1;i<=n;i++) 27 fa[i][j]=fa[fa[i][j-1]][j-1]; 28 } 29 int lca(int x,int y) 30 { 31 if (dep[x]<dep[y]) {int t=x;x=y;y=t;} 32 for (int j=20;j>=0;j--) if (dep[fa[x][j]]>=dep[y]) x=fa[x][j]; 33 if (x==y) return x; 34 for (int j=20;j>=0;j--) if (fa[x][j]!=fa[y][j]) x=fa[x][j],y=fa[y][j]; 35 return fa[x][0]; 36 } 37 struct List{bool sig,add;int v,next;}list[maxn*4];int eve[maxn],ll=2; 38 void addeve(int x,bool sig,bool add,int v) 39 { 40 List &l=list[ll];l.sig=sig;l.add=add;l.v=v; 41 l.next=eve[x];eve[x]=ll++; 42 } 43 int wa[maxn],pos[maxn*2],neg[maxn*2],ans[maxn]; 44 void play(int x,int f) 45 { 46 ans[x]=pos[wa[x]+dep[x]]+neg[wa[x]-dep[x]+n]; 47 for (int i=first[x];i;i=edge[i].next) 48 { 49 const Edge &e=edge[i]; 50 if (e.to!=f) play(e.to,x); 51 } 52 for (int i=eve[x];i;i=list[i].next) 53 { 54 const List &e=list[i]; 55 if (e.sig) pos[e.v]+=e.add?1:-1; 56 else neg[e.v]+=e.add?1:-1; 57 } 58 ans[x]=pos[wa[x]+dep[x]]+neg[wa[x]-dep[x]+n]-ans[x]; 59 } 60 int x,y; 61 int main() 62 { 63 scanf("%d%d",&n,&m); 64 memset(first,0,sizeof(first)); 65 memset(eve,0,sizeof(eve)); 66 for (int i=1;i<n;i++) 67 { 68 scanf("%d%d",&x,&y); 69 insert(x,y); 70 } 71 dfs(n/2+3,0);makef(); 72 for (int i=1;i<=n;i++) scanf("%d",&wa[i]); 73 for (int i=1;i<=m;i++) 74 { 75 scanf("%d%d",&x,&y); 76 int l=lca(x,y),d=dep[x]+dep[y]-2*dep[l]; 77 addeve(x,1,1,dep[x]); 78 addeve(y,0,1,d-dep[y]+n); 79 addeve(l,1,0,dep[x]); 80 addeve(fa[l][0],0,0,d-dep[y]+n); 81 } 82 memset(pos,0,sizeof(pos)); 83 memset(neg,0,sizeof(neg)); 84 play(n/2+3,0); 85 for (int i=1;i<n;i++) printf("%d ",ans[i]);printf("%d",ans[n]); 86 return 0; 87 }
自测在vijos上取n/2+3为根可以通过所有的点。
