一傻逼题调了两天。。
n<=30 * m<=30的地图,0表示可以放平台,1表示本来有平台,2表示不能走,3起点4终点,走路方式为象棋的日字,求:从起点走到终点,至少要放多少平台,以及放平台的方案数,无解-1。
方法一:其实能走直接平台的就可以直接走来走去,也就是算一个联通块。类似于tarjan,先把一大块缩成一点,然后连边走最短路。
错误!存在边权为0的边,会导致统计方案出现重复。比如:
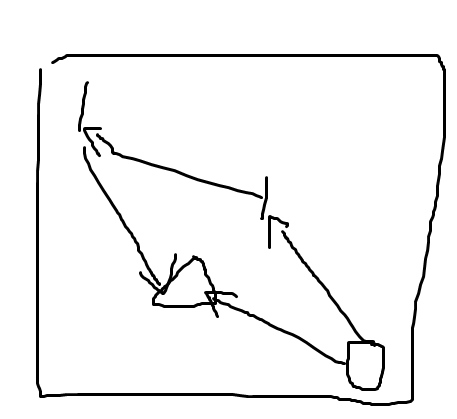
圆圈走到三角形,直接走和绕一圈是一样的,但算了两次。
方法二:把0边去掉就行了。由于数据小,开个数组[a][b][c][d]表示a,b到c,d是否能通过填一块到达,这个数组只需对每个点做一次搜索就能出来。最后就是最短路啦。
不过边权为1,谁最短路会写迪杰呢?肯定bfs啦!

1 #include<stdio.h> 2 #include<string.h> 3 #include<stdlib.h> 4 #include<algorithm> 5 //#include<iostream> 6 using namespace std; 7 8 int n,m; 9 int a[33][33],can[33][33][33][33]; 10 #define maxn 1011 11 #define maxm 10011 12 struct Edge{int tx,ty,next;}edge[maxn*maxn];int first[33][33],le=2; 13 #define LL long long 14 void in(int sx,int sy,int tx,int ty) 15 { 16 Edge &e=edge[le]; 17 e.tx=tx;e.ty=ty; 18 e.next=first[sx][sy]; 19 first[sx][sy]=le++; 20 } 21 int nx,ny; 22 const int dx[]={1,1,2,2,-1,-1,-2,-2},dy[]={2,-2,1,-1,2,-2,1,-1}; 23 bool vis[33][33]; 24 void dfs(int x,int y) 25 { 26 vis[x][y]=1; 27 for (int i=0;i<8;i++) 28 { 29 const int xx=x+dx[i],yy=y+dy[i]; 30 if (xx<1 || xx>n || yy<1 || yy>m || can[nx][ny][xx][yy] 31 || a[xx][yy]==2 || vis[xx][yy]) continue; 32 if (a[xx][yy]==0 || a[xx][yy]==4) 33 { 34 can[nx][ny][xx][yy]=1; 35 continue; 36 } 37 dfs(xx,yy); 38 } 39 } 40 const int inf=0x3f3f3f3f; 41 int dis[33][33];LL way[33][33]; 42 struct qnode{int x,y;}q[maxn];int head,tail; 43 void bfs(int sx,int sy) 44 { 45 head=0;tail=1;q[0].x=sx;q[0].y=sy; 46 for (int i=1;i<=n;i++) 47 for (int j=1;j<=m;j++) 48 dis[i][j]=inf; 49 dis[sx][sy]=0;way[sx][sy]=1; 50 while (head!=tail) 51 { 52 const int nx=q[head].x,ny=q[head++].y; 53 for (int i=first[nx][ny];i;i=edge[i].next) 54 { 55 const Edge &e=edge[i]; 56 if (dis[e.tx][e.ty]>dis[nx][ny]+1) 57 { 58 dis[e.tx][e.ty]=dis[nx][ny]+1; 59 way[e.tx][e.ty]=way[nx][ny]; 60 q[tail].x=e.tx,q[tail++].y=e.ty; 61 } 62 else if (dis[e.tx][e.ty]==dis[nx][ny]+1) 63 way[e.tx][e.ty]+=way[nx][ny]; 64 } 65 } 66 } 67 int main() 68 { 69 scanf("%d%d",&n,&m); 70 int sx,sy,tx,ty; 71 for (int i=1;i<=n;i++) 72 for (int j=1;j<=m;j++) 73 { 74 scanf("%d",&a[i][j]); 75 if (a[i][j]==3) sx=i,sy=j; 76 if (a[i][j]==4) tx=i,ty=j; 77 } 78 for (int i=1;i<=n;i++) 79 for (int j=1;j<=m;j++) 80 { 81 memset(can[i][j],0,sizeof(can[i][j])); 82 memset(vis,0,sizeof(vis)); 83 if (a[i][j]==2) continue; 84 nx=i;ny=j; 85 dfs(i,j); 86 } 87 memset(first,0,sizeof(first)); 88 for (int i=1;i<=n;i++) 89 for (int j=1;j<=m;j++) 90 for (int k=1;k<=n;k++) 91 for (int l=1;l<=m;l++) 92 { 93 if (can[i][j][k][l]) 94 { 95 in(i,j,k,l); 96 } 97 } 98 bfs(sx,sy); 99 if (dis[tx][ty]==inf) puts("-1"); 100 else printf("%d %lld ",dis[tx][ty]-1,way[tx][ty]); 101 return 0; 102 }
