BZOJ1722: [Usaco2006 Mar] Milk Team Select 产奶比赛

n<=500的树上有点权（有正负），选若干个点使点权和>=X(<=1e6)并且相邻点的对数最多，输出相邻点最多多少对。

在n个点里选某权和的最多相邻点->在n个点里选某数量的相邻点使权和最大

f(i,j,0/1)--子树i中选j对相邻关系，不选/选择节点i的最大权和，

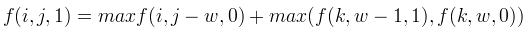
就是个背包嘛。不过注意一下背包枚举顺序即可。

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
//#include<queue>
//#include<iostream>
using namespace std;

int n,X;
#define maxn 1011
struct Edge{int to,next;}edge[maxn];int first[maxn],le=2,val[maxn];
void in(int x,int y) {Edge &e=edge[le];e.to=y;e.next=first[x];first[x]=le++;}
void insert(int x,int y) {in(x,y);in(y,x);}
int f[maxn][maxn][2];
int x;
const int inf=0x3f3f3f3f;
void dp(int x,int fa)
{
    for (int i=1;i<=n;i++) f[x][i][0]=f[x][i][1]=-inf;
    for (int i=first[x];i;i=edge[i].next)
    {
        const Edge &e=edge[i];if (e.to==fa) continue;
        dp(e.to,x);
        for (int j=n;j>=0;j--)
            for (int k=0;k<=j;k++)
            {
                f[x][j][1]=max(f[x][j][1],f[x][j-k][1]+max(k==0?-inf:f[e.to][k-1][1],f[e.to][k][0]));
                f[x][j][0]=max(f[x][j][0],f[x][j-k][0]+max(f[e.to][k][1],f[e.to][k][0]));
            }
    }
    for (int j=n;j>=0;j--) f[x][j][1]+=val[x];
}
int main()
{
    scanf("%d%d",&n,&X);
    for (int i=1;i<=n;i++)
    {
        scanf("%d%d",&val[i],&x);
        insert(x,i);
    }
    dp(0,-1);
    int ans=n;
    for (;ans>=0;ans--) if (f[0][ans][0]>=X) break;
    printf("%d
",ans);
    return 0;
}