n<=300个人,每个人的视野是他前面比他严格矮的人数+1,问所有排列中的期望视野总数,高度<=1000。
首先,期望的线性性质,把总视野分成每个人的视野加起来。枚举每个人看贡献。
方法一:枚举一个人,然后枚举他前面有多少人。注意这里可能有两种情况,一种是他前面没有比他高的人,另一种反之,分开计算。如果s表示比这个人矮的个数,那么第一种是$sum_{j=0}^s frac{A_s^j * (n-j+1)! * (j+1)}{n!}$,第二种是$sum_{j=0}^s frac{A_s^j*(n-s-1)(挑个比他高的放前面)*(n-j-2)!*(n-j-1)(剩下(n-j-2)人乱排后,下图中一坨扔到(n-j-2)人形成的(n-j-2+1)个空位)*(j+1)}{n!}$。

1 #include<cstring> 2 #include<cstdlib> 3 #include<cstdio> 4 //#include<assert.h> 5 #include<algorithm> 6 #include<iostream> 7 #include<iomanip> 8 using namespace std; 9 10 int n; 11 #define double long double 12 #define maxn 311 13 #define maxb 1011 14 int a[maxn],bud[maxb]; 15 double frac[maxn]; 16 void pre(int n) {frac[0]=1; for (int i=1;i<=n;i++) frac[i]=frac[i-1]*i;} 17 double A(int n,int m) {return frac[n]/frac[n-m];} 18 int main() 19 { 20 scanf("%d",&n); pre(n); 21 for (int i=1;i<=n;i++) scanf("%d",&a[i]),bud[a[i]]++; 22 double ans=0; 23 for (int i=0,s=0;i<=1000;i++) if (bud[i]) 24 { 25 double tmp=0; 26 for (int j=0;j<=s;j++) 27 tmp+=A(s,j)/frac[n]*frac[n-j-1]*(j+1); 28 for (int j=0,to=min(s,n-2);j<=to;j++) 29 tmp+=(j+1)*A(s,j)/frac[n]*(n-s-1)*frac[n-j-2]*(n-j-1); 30 ans+=bud[i]*tmp; 31 s+=bud[i]; 32 } 33 cout<<fixed<<setprecision(2)<<ans<<endl; 34 return 0; 35 }
方法二:可以证明每个人的贡献是$frac{n+1}{n-s_i+1}$,其中$s_i$是比i矮的人数。
现在就考虑j对i有1个贡献的情形吧,这样想,先把(n-s)个>=i(包括i自己)的人在序列里放好,然后一个比i矮的j插到i前面,剩下的$(s_i-1)$个比i矮的乱排。如图:
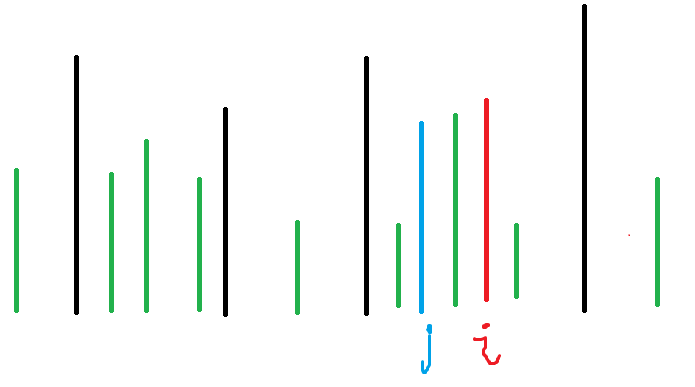
其他的$(s_i-1)$不管怎么乱排都无法影响j对i产生1个贡献。所以i对答案的贡献是$frac{s_i*(n-s_i)!*A_{n}^{s_i-1}}{n!}+1(自带的)$,整理下就是$frac{n+1}{n-s_i+1}$。O(n)搞定。
