给个点权树以下操作:两点连边,若已联通则无视;两点删边,若边不存在则无视;一条链加上某个数;以及!!!
查询一条链上任选一条子链的期望权值,一条链的权值为链上所有点的权值的和。
好吧前面三个都是LCT普通操作,第四个呢。。。其实只要会分治地求答案,即合并一个区间的左子区间和右子区间的答案即可。
YY一下可得:一个区间的数字摆在一起,叫做$a_1,a_2,……,a_n$,然后他们的期望就是:$frac{sum_{i=1}^{n}a_i*i*(n-i+1)}{frac{n(n+1)}{2}}$。
下面那部分知道链长度即可,问题是上面那部分要做区间合并还支持区间修改。
看怎么并:
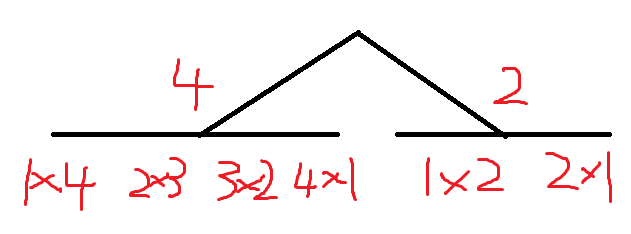
一开始各项系数长这样。然后并起来之后变成:
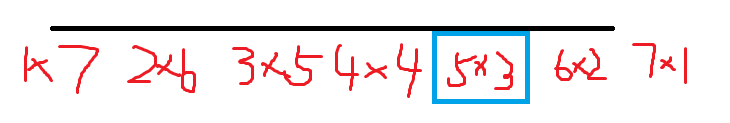
可以发现左边那部分多了:$3*(1*a_1+2*a_2+……)$,右边那部分多了:$5*(2*a_1+1*a_2)$。
所以就要记一个$lsum=1*a_1+2*a_2+……+n*a_n$,$rsum=n*a_1+(n-1)*a_2+……+1*a_n$,in this way $this->exp=lson->exp+lson->lsum*(rson->size+1)+rson->exp+rson->rsum*(lson->size+1)+(lson->size+rson->size+1)*this->num$。
然后lsum和rsum就很容易合并啦~
然后看怎么加,首先lsum和rsum都是加上$x*frac{n(n+1)}{2}$,而exp要加上$x*(1*n+2*(n-1)+……+n*1)$,这坨东西可以把n-1,n-2……的括号拆掉,然后分成两部分推出来,是:$x*frac{n(n+1)(n+2)}{6}$。完美。

1 #include<string.h> 2 #include<stdlib.h> 3 #include<stdio.h> 4 #include<math.h> 5 //#include<assert.h> 6 #include<algorithm> 7 //#include<iostream> 8 //#include<bitset> 9 using namespace std; 10 11 int n,m; 12 #define maxn 50011 13 #define LL long long 14 LL gcd(LL a,LL b) {return b?gcd(b,a%b):a;} 15 struct LCT 16 { 17 struct Node 18 { 19 int fa,son[2]; 20 bool rev; 21 LL v,lsum,sum,rsum,exp; int add,size; 22 }a[maxn]; 23 void makeatree(int id,int v) 24 { 25 a[id].fa=a[id].son[0]=a[id].son[1]=a[id].rev=0; a[id].size=1; 26 a[id].lsum=a[id].rsum=a[id].v=a[id].sum=a[id].exp=v; a[id].add=0; 27 } 28 void up(int x) 29 { 30 if (!x) return; 31 int &p=a[x].son[0],&q=a[x].son[1]; 32 a[x].size=a[p].size+a[q].size+1; 33 a[x].sum=a[p].sum+a[q].sum+a[x].v; 34 a[x].lsum=a[p].lsum+a[q].lsum+(a[p].size+1)*(a[x].v+a[q].sum); 35 a[x].rsum=a[p].rsum+a[q].rsum+(a[q].size+1)*(a[x].v+a[p].sum); 36 a[x].exp=a[p].exp+a[q].exp+(a[p].size+1)*a[q].rsum+(a[q].size+1)*a[p].lsum 37 +(a[p].size+1)*a[x].v*(a[q].size+1); 38 } 39 void addsingle(int x,int v) 40 { 41 if (!x) return; 42 a[x].add+=v; a[x].v+=v; 43 a[x].sum+=a[x].size*1ll*v; 44 a[x].lsum+=(((a[x].size+1)*1ll*a[x].size)>>1)*v; 45 a[x].rsum+=(((a[x].size+1)*1ll*a[x].size)>>1)*v; 46 a[x].exp+=(1ll*a[x].size*(a[x].size+1)*(a[x].size+2))/6*v; 47 } 48 void revsingle(int x) 49 { 50 if (!x) return; 51 a[x].rev^=1; 52 a[x].son[0]^=a[x].son[1]; a[x].son[1]^=a[x].son[0]; a[x].son[0]^=a[x].son[1]; 53 a[x].lsum^=a[x].rsum; a[x].rsum^=a[x].lsum; a[x].lsum^=a[x].rsum; 54 } 55 void down(int x) 56 { 57 int &p=a[x].son[0],&q=a[x].son[1]; 58 if (a[x].rev) {revsingle(p); revsingle(q); a[x].rev=0;} 59 if (a[x].add) {addsingle(p,a[x].add); addsingle(q,a[x].add); a[x].add=0;} 60 } 61 bool isroot(int x) 62 { 63 if (!a[x].fa) return 1; 64 return (a[a[x].fa].son[0]!=x && a[a[x].fa].son[1]!=x); 65 } 66 int sta[maxn]; 67 void download(int x) 68 { 69 int top=0; for (;!isroot(x);x=a[x].fa) sta[++top]=x; sta[++top]=x; 70 for (;top;top--) down(sta[top]); 71 } 72 void rotate(int x) 73 { 74 const int y=a[x].fa,z=a[y].fa; 75 bool w=(x==a[y].son[0]); 76 a[x].fa=z; 77 if (!isroot(y)) a[z].son[y==a[z].son[1]]=x; 78 a[y].son[w^1]=a[x].son[w]; 79 if (a[x].son[w]) a[a[x].son[w]].fa=y; 80 a[x].son[w]=y; 81 a[y].fa=x; 82 up(y); up(z); 83 } 84 void splay(int x) 85 { 86 if (!x) return; 87 download(x); 88 while (!isroot(x)) 89 { 90 const int y=a[x].fa,z=a[y].fa; 91 if (!isroot(y)) 92 { 93 if ((x==a[y].son[0])^(y==a[z].son[0])) rotate(x); 94 else rotate(y); 95 } 96 rotate(x); 97 } 98 up(x); 99 } 100 void access(int x) 101 { 102 int y=0,tmp=x; 103 while (x) {splay(x); a[x].son[1]=y; up(x); y=x; x=a[x].fa;} 104 splay(tmp); 105 } 106 void resetroot(int x) 107 { 108 access(x); 109 revsingle(x); 110 } 111 void link(int x,int y) 112 { 113 resetroot(x); 114 a[x].fa=y; 115 } 116 void cut(int x,int y) 117 { 118 resetroot(x); 119 access(y); 120 if (a[y].son[0]!=x || a[x].son[1]) return; 121 a[y].son[0]=a[x].fa=0; 122 up(y); 123 } 124 int findroot(int x) 125 { 126 while (a[x].fa) x=a[x].fa; 127 return x; 128 } 129 void add(int x,int y,int v) 130 { 131 resetroot(x); 132 access(y); 133 addsingle(y,v); 134 } 135 void query(int x,int y) 136 { 137 if (findroot(x)!=findroot(y)) {puts("-1"); return;} 138 resetroot(x); 139 access(y); 140 LL p=a[y].exp,q=(a[y].size+1ll)*a[y].size/2,d=gcd(p,q); 141 printf("%lld/%lld ",p/d,q/d); 142 } 143 }t; 144 145 int main() 146 { 147 scanf("%d%d",&n,&m); 148 for (int i=1,v;i<=n;i++) scanf("%d",&v),t.makeatree(i,v); 149 for (int i=1,x,y;i<n;i++) 150 { 151 scanf("%d%d",&x,&y); 152 t.link(x,y); 153 } 154 int id,x,y,z; 155 while (m--) 156 { 157 scanf("%d",&id); 158 if (id==1) 159 { 160 scanf("%d%d",&x,&y); 161 t.cut(x,y); 162 } 163 else if (id==2) 164 { 165 scanf("%d%d",&x,&y); 166 if (t.findroot(x)!=t.findroot(y)) t.link(x,y); 167 } 168 else if (id==3) 169 { 170 scanf("%d%d%d",&x,&y,&z); 171 if (t.findroot(x)==t.findroot(y)) t.add(x,y,z); 172 } 173 else if (id==4) 174 { 175 scanf("%d%d",&x,&y); 176 t.query(x,y); 177 } 178 } 179 return 0; 180 }
