转自:https://zhidao.baidu.com/question/494249074914968332.html
SVM使用拉格朗日乘子法更为高效地求解了优化问题。
SVM将寻找具有最大几何间隔划分超平面的任务转化成一个凸优化问题,如下所示:
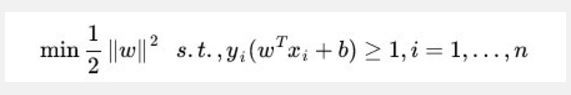
//其中,“s.t.”,指 subject to,受限制于...。学到了!
我们当然可以直接使用现成工具求解,但还有更为高效的方法,那就是使用拉格朗日乘子法将原问题转化为对偶问题求解。
具体做法是:
(1)将约束融入目标函数中,得到拉格朗日函数;
(2)然后对模型参数w和b求偏导,并令之为零;
(3)得到w后,将其带入拉格朗日函数中,消去模型参数w和b;
(4)这样就得到了原问题的对偶问题,对偶问题和原问题等价,同时对偶问题也是一个凸优化问题,使用SMO算法求解拉格朗日乘子;
(5)得到拉格朗日乘子后,进一步可以得到模型参数w和b,也就得到了我们想要的划分超平面。
2020-5-25更新——————————
1.为什么要从原始问题转换为对偶问题?
https://www.cnblogs.com/crackpotisback/p/8674534.html,给出了这三点,但是该怎么理解呢?

1的话是不是因为凸二次规划问题如果存在不等式约束,它是不好求解的?搜了一下“不等式优化问题”,果然是我知识存在盲区啊!没学过这个啊!
https://www.cnblogs.com/BlueBlueSea/p/10032417.html,我以前居然学过,但是过去太久了,而且我当时肯定都没看明白,那个时候搜索信息的能力真是差劲啊!怎么就搜到百度文库,就看一个百度文库,就想把问题给理解了?我那个时候效率可真差劲啊!现在就好多了。
2.等式约束优化、不等式约束优化
链接,这个讲的真的很好!系统又简单。
对于等式约束问题,有消元法、拉格朗日乘子法;后者是针对高维、多次、非线性约束方程的。
对于不等式约束优化问题,包括的知识点是拉格朗日乘子法和KKT条件,但是不等式转换可能获取到的解不是真正的解,那么就有了KKT条件验证(具体没有看懂)?

针对凸规划问题,是充要条件。原来整个构造的是拉格朗日函数,那个λ是K-T乘子符号。
因为针对凸优化不等式约束问题,它的解法数学模型就可以通过构架拉格朗日函数来求解。
3.什么是对偶问题?
https://www.zhihu.com/question/58584814/answer/159863739,这里面给的几个图简直太牛了。就能更直观地理解什么是等式约束、不等式约束问题了。
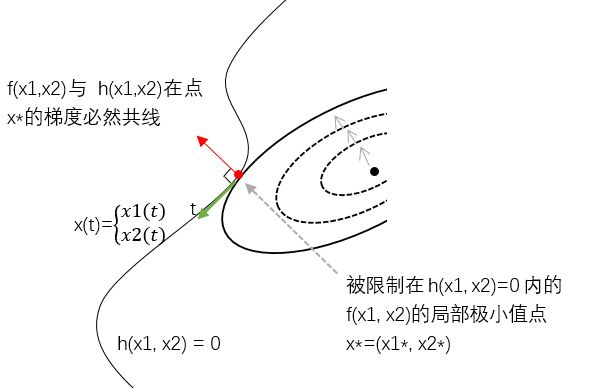
等式约束,在线上

一个不等式约束

两个不等式约束,求交集
其实我的问题是,对偶到底指的是什么?为什么要叫对偶呢?(dual problem)
https://www.zhihu.com/question/58584814,这个问题下一个回答说“比如通过函数值集合理解、鞍点解释、博弈解释和经济学解释等”,这个我就不太明白了。好难理解,我放弃理解。
4. max下面有个x
//我发现我居然是不知道这个的意思,我数学基础也真的太差了。
https://zhidao.baidu.com/question/878646357027684732.html

需要从内往外看,max是指固定住x,求λ使得L的值最大,然后min是固定住求好的λ,求使得L值最小的x。绝了。
5.凸函数和凹函数
https://blog.csdn.net/zhangdongren/article/details/84671235
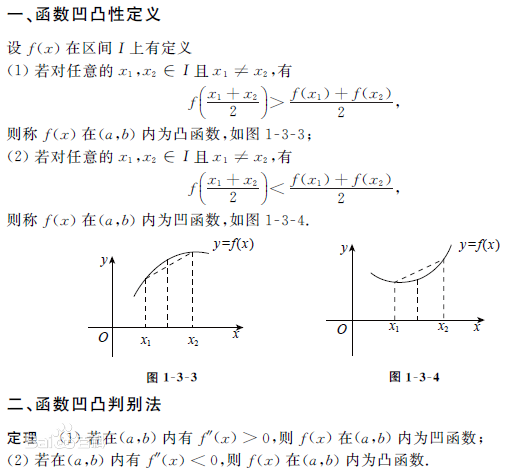
简单来说就是上凸和下凹,这个是同济教材上的规定,是和国际上相反的。
二阶导数>0,则在这个区间中是凹;<0,则是凸。
其实就是在一个区间内,直接看它的函数形状就可以了。
6.仿射函数
//知乎上有好多讲放射函数的!一大堆!我要吸收一下。
6.1什么是仿射affine?
https://www.zhihu.com/question/20666664/answer/157400568,讲的非常好。
仿射变换=线性变换+平移
线性变换特点:①直线比例不变化,②变换前是直线,变换之后还是直线,③变换前是原点,变换后依旧是原点。
仿射特点:①直线比例不变化,②变换前是直线,变换之后还是直线。(没有③是因为它有了平移的这一步)
注意到我们以前学的y=ax+b这样其实它不是一个线性函数,因为它不仅包括线性变换,还包括了平移变换,它是一个仿射变换,从一维到一维。
而y=Ax+b这样的表示,A可以是一个矩阵或者更高维度的?线性空间也有n维的空间(高维空间中的直线?我最多只能理解三维空间中的直线),

从k->m维的空间映射。
总的来说,仿射函数的作用就是进行高维空间的映射吧。
7.推导大体过程
SVM的原问题是一个有不等式约束的凸优化问题,那么可以通过拉格朗日乘子法转换为对偶问题,对偶问题更好解决,SVM中原问题是通过极小极大来解决,对偶问题是转换为了极大极小,而对偶问题等价于原问题需要满足严格条件或KKT条件,这样的称为硬对偶;这样的话就首先对W/b求偏导得到公式表示带入原问题拉格朗日函数中,就变成了对乘子a求最大值的问题,可以通过SMO求解,此时也方便核函数的引入;在求解b的时候,是利用了KKT的互补约束;支持向量确定超平面也是通过KKT的等于0互补约束,如果ai=0那么不在支持向量平面上,当X^TW+b=1时,是在支持平面上,而根据W和b的计算公式,它们计算所用的点也都是SV,因为ai为0,则i项值为0.
上面写的这个是针对线性可分SVM,更复杂的有线性SVM(不一定是可分,比如引入软间隔),非线性SVM(使用了核函数)。
8.具体公式推导
https://zhuanlan.zhihu.com/p/49331510
间隔最大化公式:
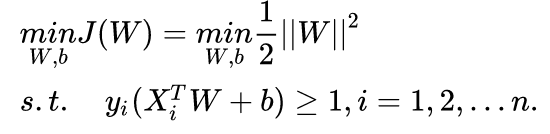
也就是原始问题,拉格朗日函数为,目标为极小化它,得到L最小化时的W/b/a:
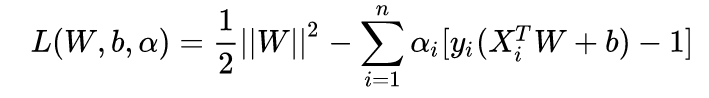
优化目标为:
![]()
这个优化目标和 间隔最大化公式 是等价的。它的对偶问题为:
![]()
转换为了极大极小问题,从内而外求解,首先是min:

将W和b代入拉格朗日函数中,化简后得:
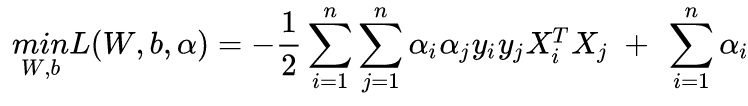
求max,加负号转换为求min:

同时约束条件是(这个约束条件是拉格朗日函数带来的):
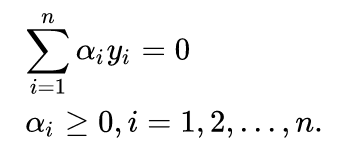
上面这个就是对偶问题的公式,需要满足严格条件和KKT条件,强对偶,二者等价。其中KKT条件为:
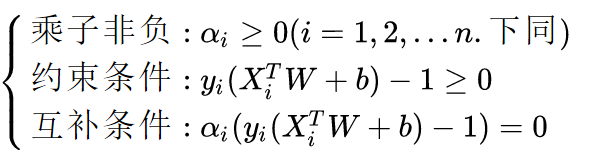
求ai是二次规划问题,可以通过SMO,假设已求得ai,那么W为:
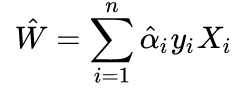
b通过互补条件来求解,至少存在一个点j使得X^TW+b=1,因为如果ai全为0,那么W为0,margin=1/||w||^2,则为无穷,间隔为无穷,是不可以的,所以至少有一个ai!=0,那么则X^TW+b=1。则b为:
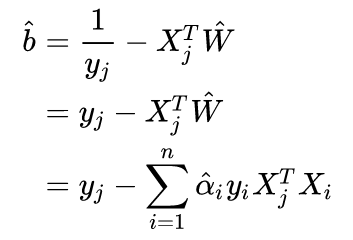
综上,分离超平面为:

分类决策函数为:
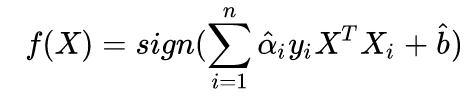
因为不在支持向量平面上的点,ai=0,所以W/b计算公式为:
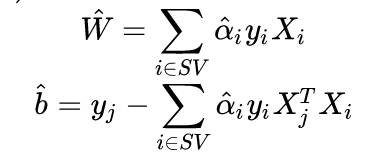
所以W/b只和SV有关,和其他点无关,那么分类超平面也只和SV点有关。
9.拉格朗日函数为什么要构建minmax?
https://www.cnblogs.com/breezezz/p/11303722.html,讲的比较详细。
针对我们构造的拉格朗日函数,如果直接对x和乘子做导数,也会很复杂,所以尝试max。
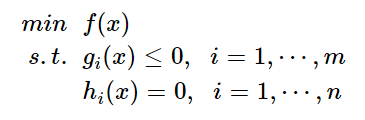
构建拉格朗日函数: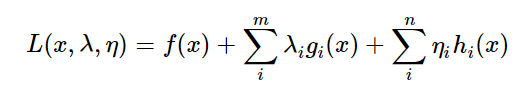
那么,

那么:

上式固定住x,求使得L最大时λ和η的值,λ的约束条件为>=0,如果存在一个不满足约束的点,gx>0,那么此时λ可以取无穷大,所以求上面的极小化问题可以分为minmax两步:
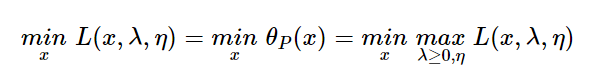
这个是原始问题,它等价于之前的拉格朗日函数,它的对偶问题是:
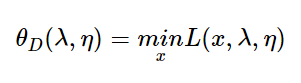
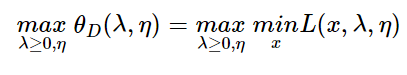
就是minmax交换,上式就是极大极小问题,约束为λ和η>=0。
10.原始问题minmax与对偶问题maxmin的关系
弱对偶强对偶没有太看懂,强对偶的话:

即两个目标函数完全相等,强对偶的两个条件:严格条件和KKT条件。
11.严格条件和KKT条件
前者即Slater条件:
https://zhuanlan.zhihu.com/p/38182879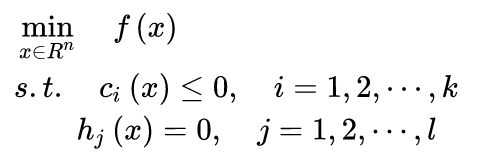

也就是不能取等号,如果这样的话就没有支持向量的点了?迷惑。
不对,上面说的是存在x,不是说所有x,是有支持向量的点的。这要求SVM是线性可分的。
“严格条件是强对偶性的充分条件,但并不是必要条件。有些不满足严格条件的可能也有强对偶性。”
KKT条件:

反正是上面的约束问题。