转自:https://blog.csdn.net/z2539329562/article/details/79187967
https://blog.csdn.net/class_brick/article/details/79724660
1.用频率估计概率

2.思想
极大似然估计可以拆成三个词,分别是“极大”、“似然”、“估计”,分别的意思如下:
极大:最大的概率
似然:看起来是这个样子的
估计:就是这个样子的
连起来就是,最大的概率看起来是这个样子的那就是这个样子的。
总结:极大似然估计就是在只有概率的情况下,忽略低概率事件直接将高概率事件认为是真实事件的思想。
3.离散
例1、离散的小球问题:
箱子里有一定数量的小球,每次随机拿取一个小球,查看颜色以后放回,已知拿到白球的概率p为0.7或者0.3,拿了三次,都不是白球,想要求拿到白球的概率的极大似然估计。
分析:此处从数学上来讲,想要准确的求出拿到白球的概率是不可能的,所以此处求的是概率的极大似然估计。而这里的有放回的拿取,是高中数学中经典的独立重复事件,可以很简单的分别求出白球概率为0.7和0.3的时候拿三次都不是白球的概率。
解:
若拿到白球的概率为0.7,拿三次都不是白球的概率为:
P_0.7=0.3*0.3*0.3=0.027
若拿到白球的概率为0.3,拿三次都不是白球的概率为:
P_0.3=0.7*0.7*0.7=0.343
P_0.3>P_0.7,可知当前情况下白球概率为0.3的概率大于白球概率为0.7
综上所述:
拿到白球的概率的极大似然估计为0.3
4.连续
连续状态依然用刚刚拿小球的例子,不过此处白球的概率不再明确为0.7-0.3,此处只知道白球的概率p的范围为0.3<=p<=1。
例2、连续的小球问题:
箱子里有一定数量的小球,每次随机拿取一个小球,查看颜色以后放回,已知拿到白球的概率p的范围是[0.3,0.7],拿了三次,都不是白球,想要求拿到白球的概率的极大似然估计。
分析:与例1相同,想要知道小球的极大似然估计,就是要先求在已知条件下,发生已知事件的概率,然后据此求出小球的极大似然估计。
解:
记拿到白球的概率为p,取白球的事件为Y,取到时Y=1,未取到时Y=0,小球颜色不是白色的事件Y重复3次的概率为:
P(Y=0;p)=(1-p)^3
欲求p的极大似然估计,即要求P(Y=0;p)的极大值:
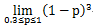
令Q(p)=(1-p)^3
Q'(p)=-3*(1-p)^2
令Q'(p)=0
求得Q的极值点为p=1,且当p<1时,Q'(p)<0,p>1时,Q'(p)<0,可知Q(p)为单调减函数
可知0.3<=p<=1的条件下,p=0.3时,Q(p)取得最大值。
综上所述:小球概率的极大似然估计为0.3
5.总结
通过极大似然估计的思想、离散形式、连续形式的分析,可以得出极大似然估计的通常解法,总体来说分为以下几步:
1、得到所要求的极大似然估计的概率p的范围
2、以p为自变量,推导出当前已知事件的概率函数式Q(p)
3、求出能使得Q(p)最大的p
这样便求出了极大似然估计值p 。