转自:https://blog.csdn.net/edogawachia/article/details/80043673
1.sigmoid
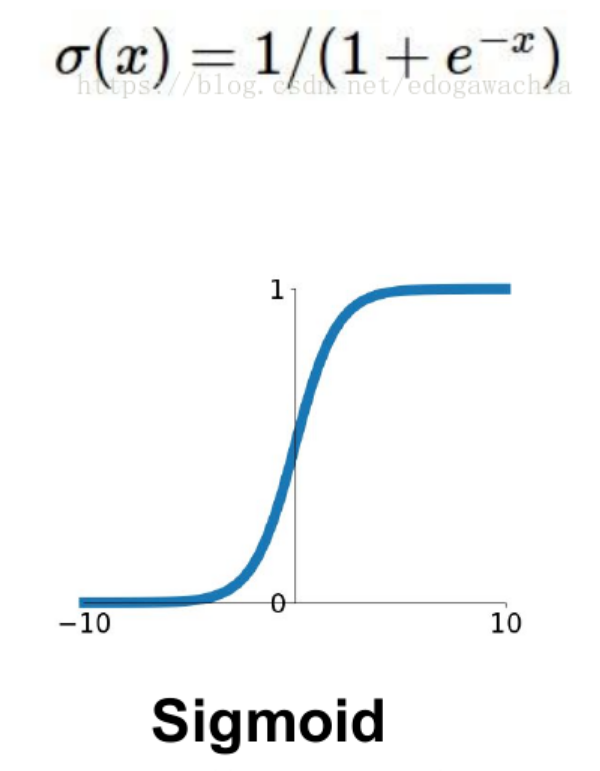
特点:可以解释,比如将0-1之间的取值解释成一个神经元的激活率(firing rate)
缺陷:
- 有饱和区域,是软饱和,在大的正数和负数作为输入的时候,梯度就会变成零,使得神经元基本不能更新。
- 只有正数输出(不是zero-centered,均值为0?),这就导致所谓的zigzag现象:

也就是说,w始终是朝着一直为正或者一直为负去变化的。

也就是说,更新只能朝着一个方向更新。
2.tanh函数
![]()
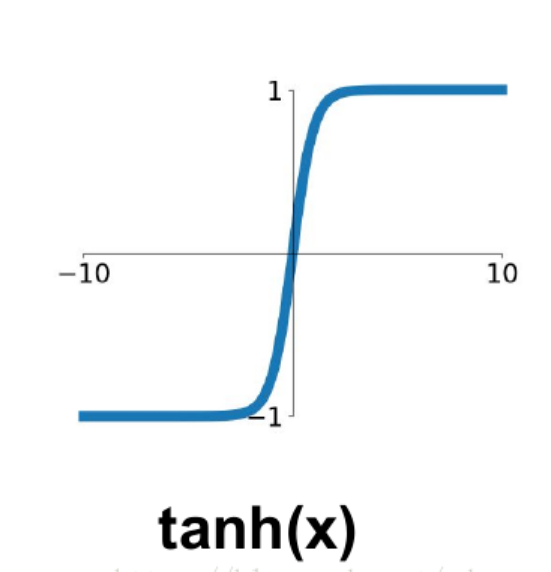
计算量大。
tanh和sigmoid函数是具有一定的关系的,可以从公式中看出,它们的形状是一样的,只是尺度和范围不同。
3.ReLU
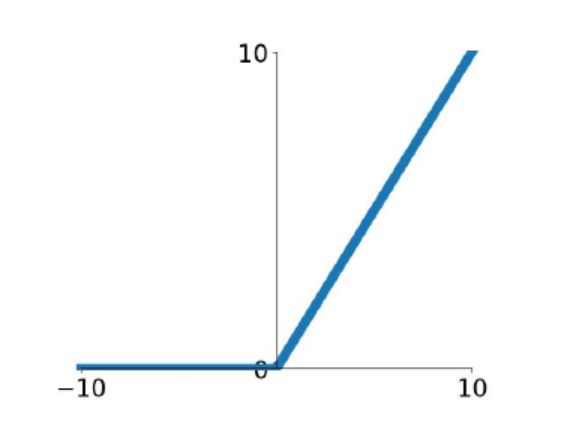
CNN中常用。对正数原样输出,负数直接置零。在正数不饱和,在负数硬饱和。relu计算上比sigmoid或者tanh更省计算量,因为不用exp,因而收敛较快。但是还是非zero-centered。
relu在负数区域被kill的现象叫做dead relu,这样的情况下,有人通过初始化的时候用一个稍微大于零的数比如0.01来初始化神经元,从而使得relu更偏向于激活而不是死掉,但是这个方法是否有效有争议。
4.LeakyReLU
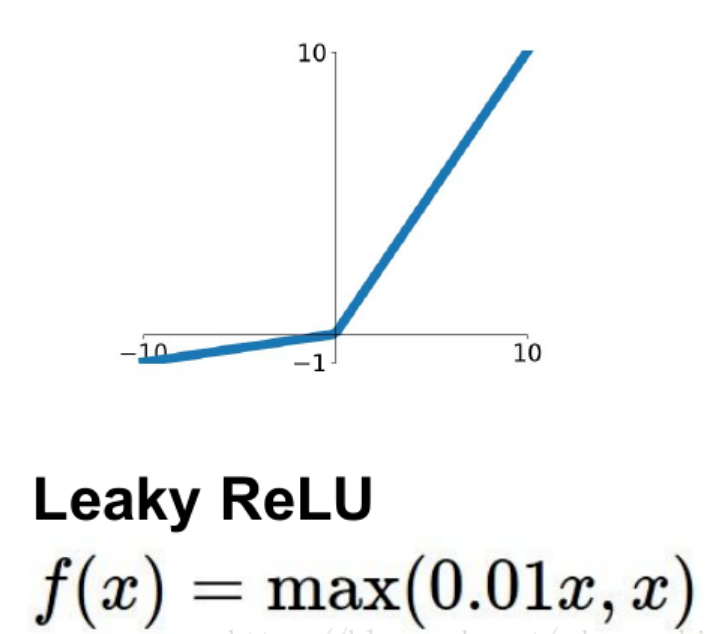
PReLU
parametric rectifier:
f(x) = max(ax,x)
但是这里的a不是固定下来的,而是可学习的。
ELU
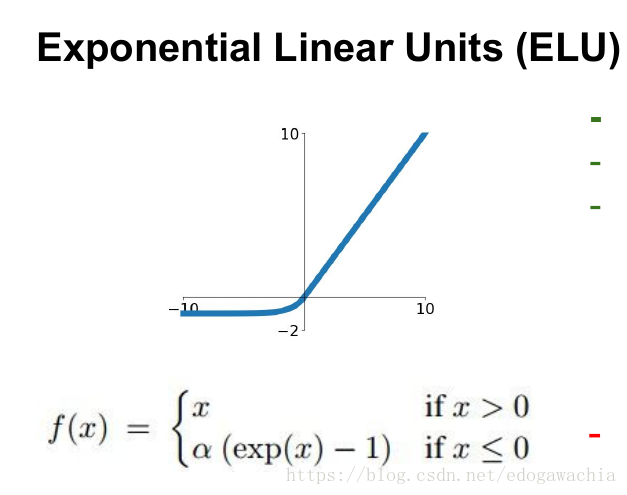
2020-5-12周二更新——————————
1.为什么通常Relu比sigmoid和tanh强,有什么不同?
https://www.cnblogs.com/zlslch/p/6970538.html
是由于梯度的原因,对于后两个,都有梯度都趋向于0的部分,(我认为是对于sigmoid当激活函数值趋向于0/1时,会出现梯度消失;对于tanh是激活函数值趋向于-1/1的时候),尤其是在网络层数多的时候,而relu在在激活函数值为正的时候,梯度是恒定的,收敛会更快;而后两者的优势主要是全程可导。relu是分段线性,求导更快。
2.为什么引入relu?
https://www.cnblogs.com/zlslch/p/6970538.html
1.计算量的问题,后两者都需要计算指数,计算量大,
2.网络深时,出现梯度消失,趋于0,会造成信息丢失,前面的网络更新慢,收敛慢
3.第三,Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生
多加一句,现在主流的做法,会在做完relu之后,加一步batch normalization,尽可能保证每一层网络的输入具有相同的分布。(BN这个原理我还不了解。